1. 引言
在计算机辅助几何设计(Computer Aided Geometric Design CAGD)和数字几何设计领域中,细分曲面和非均匀有理B样条(简称NURBS)已成为曲面造型的主流。尽管非均匀有理B样条已经是一种工业标准并且很容易的应用到商业建模系统中,但是由于NURBS需要矩形网格的限制,仅仅使用它通常难以构造一些复杂的曲面,而细分曲面的出现有效的弥补了这些问题。
对于细分曲面,Prautzsch [1] 在1998年提出了均匀节点区间的任意次数细分法,2001年Warren等一些学者[2] -[4] 推广了Prautzsch的结果,但是这些细分方法中没有一种是非均匀的细分方法[5] ,因此,在几何建模的通用性和灵活性方面存在一定的局限性。2007年,Thomas等人[6] 提出了基于Schaefer的节点插入[7] 的非均匀细分算法,然而该算法在曲面包含奇异点时会带来困难。对于N边洞填充的问题,文献[8] 用N张双7次NURBS曲面去构造几乎处处 连续的N边域曲面,这种方法通过两步计算实现,需要较高的计算耗费;文献[9] 用流形的方法构造N边域曲面,虽然生成的曲面处处
连续的N边域曲面,这种方法通过两步计算实现,需要较高的计算耗费;文献[9] 用流形的方法构造N边域曲面,虽然生成的曲面处处 连续,但这种方法构造出的曲面赋值比较繁琐;文献[10] 的方法只适合于均匀三次B样条曲面的情况;在文献[11] 中给出了非均匀Catmull-Clark细分模式产生N边域曲面的方法,但由于细分混合曲面必须与基曲面片共用三排控制顶点,因此对围成N边洞的曲面片要求较高,所以应用范围受到一定的限制,文献[11] 也未涉及多边洞填充问题。针对以上情况,本文将细分曲面运用于对传统NURBS参数曲面进行拼接以及对N片NURBS参数曲面围成的N边洞进行连续填充,提出一类边界处理规则用以生成插值于角点的非均匀Catmull-Clark细分曲面,并利用插值于角点的非均匀Catmull-Clark细分曲面进行N边洞
连续,但这种方法构造出的曲面赋值比较繁琐;文献[10] 的方法只适合于均匀三次B样条曲面的情况;在文献[11] 中给出了非均匀Catmull-Clark细分模式产生N边域曲面的方法,但由于细分混合曲面必须与基曲面片共用三排控制顶点,因此对围成N边洞的曲面片要求较高,所以应用范围受到一定的限制,文献[11] 也未涉及多边洞填充问题。针对以上情况,本文将细分曲面运用于对传统NURBS参数曲面进行拼接以及对N片NURBS参数曲面围成的N边洞进行连续填充,提出一类边界处理规则用以生成插值于角点的非均匀Catmull-Clark细分曲面,并利用插值于角点的非均匀Catmull-Clark细分曲面进行N边洞 连续填充。
连续填充。
2. 非均匀Catmull-Clark细分模式与轮廓删除法
2.1. 非均匀Catmull-Clark细分模式[11]
Catmull-Clark细分方法是三次B样条曲线细分向任意拓扑网格上曲面细分的推广,采用四边形1~4面分裂拓扑规则生成新网格的拓扑,包括几何规则和拓扑规则,在正规网格处产生双三次B样条曲面,该曲面除奇异顶点外处处 连续[12] 。非均匀Catmull-Clark细分模式与Catmull-Clark细分模式的拓扑规则一样,但新点的计算公式如下:
连续[12] 。非均匀Catmull-Clark细分模式与Catmull-Clark细分模式的拓扑规则一样,但新点的计算公式如下:
新面点:
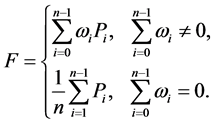 (1)
(1)
其中,
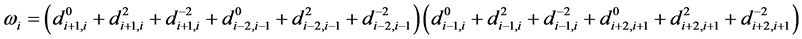
新边点: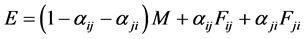 。
。
其中,
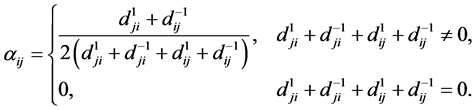
 (2)
(2)
新顶点:
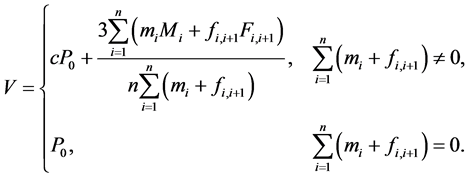 (3)
(3)
其中,
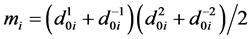 ,
, ,
, ,
, 的计算推导与(2)式中的
的计算推导与(2)式中的 相同,
相同, 的计算推导与(1)式
的计算推导与(1)式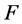 相同。
相同。
在上面的公式中, ,
, 为参数,
为参数, 与边
与边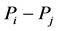 对应,
对应, 表示该边绕
表示该边绕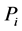 逆时针旋转遇到的第
逆时针旋转遇到的第 条边。新网格中各边参数赋予的规则表示如图1所示。
条边。新网格中各边参数赋予的规则表示如图1所示。
2.2. 轮廓删除法
轮廓删除法(Skirt-removed approach)的思想就是每次细分时,边界边不产生新边点,边界点不产生新顶点点。它可以分两步进行:
1) 采用普通的Catmull-Clark细分模式生成过渡网格,计算出每个面对应的新面点,每条内部边对应的新边点,每个内部顶点对应的新顶点,再将所有新点按照细分拓扑规则连成一个新网格;
2) 把过渡网格上的轮廓即所有边界点、边界边、边界面及与边界点相连的内部边删除。
引入轮廓删除法是为了把Catmull-Clark细分模式应用于开网格(带有边界的二维流行[11] ),开网格的轮廓是指网格上的所有边界面及其上的顶点、边所形成的子网格,对开网格删除轮廓是指在删除轮廓的同时,还要保留轮廓与内部面的公共边,这些被保留的公共边就是新网格的边界边。
为实现对NURBS曲面的混合和填充,关键是对开网格的边界做适当的处理,以使细分曲面插值于基曲面片的边界曲线,并满足一定的连续性要求。
3. NURBS曲面混合与N边洞填充
本节首先讨论NURBS曲面片的混合问题,然后构造插值于角点的非均匀Catmull-Clark细分曲面,再通过适当的处理,将得到的曲面统一到轮廓删除模式下的非均匀Catmull-Clark细分曲面,最后对非均匀Catmull-Clark细分曲面的N边洞进行G1填充。
3.1. 曲面混合
给定N片双三次非均匀B样条曲面为基曲面片,记第k片曲面Pk的控制网格为: (
( ;
; ),相应的单节点向量为:
),相应的单节点向量为: ,
,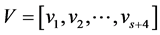 ,要求构造出的细分曲面片与Pk沿第一行(i = 1)控制顶点所确定的边界光滑拼接。假定每片都由
,要求构造出的细分曲面片与Pk沿第一行(i = 1)控制顶点所确定的边界光滑拼接。假定每片都由 的控制网格确定,初始输入如图2 (黑点以外的部分)所示。
的控制网格确定,初始输入如图2 (黑点以外的部分)所示。
首先,为了使混合曲面与每片基曲面Pk的拼接达到C2连续,初始控制网格应与Pk的控制网格共用三行顶点: 得到
得到 个
个 网格片,增加一些新点把这些网格片连接成一个完整的控制网格,其增加点的规则如下:
网格片,增加一些新点把这些网格片连接成一个完整的控制网格,其增加点的规则如下:
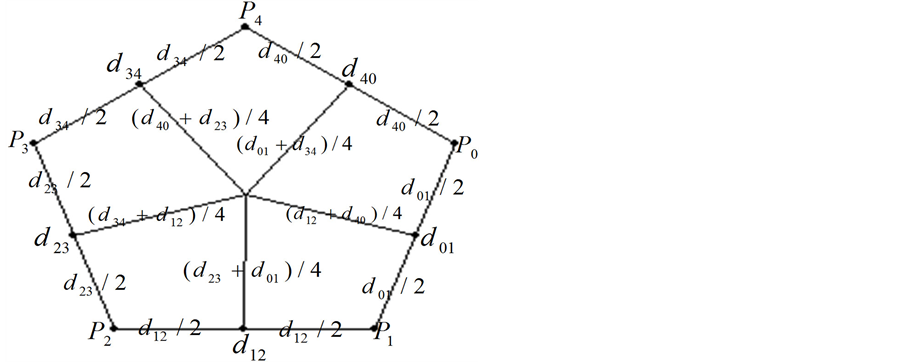
Figure 1. New rules of boundary parameters
图1. 新边参数赋予的规则
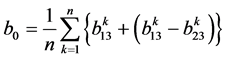
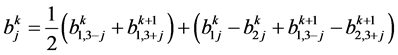
然后,对控制网格进行预处理,方法如下:
记细分混合曲面的控制网格为 ,取出其与Pk公共的三排控制顶点,并加入相应的延伸边以及
,取出其与Pk公共的三排控制顶点,并加入相应的延伸边以及 中与Pk相邻的边,记为
中与Pk相邻的边,记为 ,设置
,设置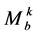 各边权值如下:
各边权值如下:
1) 同一列上的水平边所对应的权值为: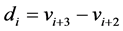 ,
, ;同时,延伸层中靠近第一列水平边(权值为
;同时,延伸层中靠近第一列水平边(权值为 )的边权值设为
)的边权值设为 ,延伸层中靠近最后一列水平边(权值为
,延伸层中靠近最后一列水平边(权值为 )的边权值设为
)的边权值设为 .
.
2) 同一行上的竖直边所对应的权值为: ,
, ;同时,
;同时, 中与基曲面Pk相邻的各边权值设为
中与基曲面Pk相邻的各边权值设为 ,延伸层中靠近最后一行竖直边(权值为
,延伸层中靠近最后一行竖直边(权值为 )的边权值设为
)的边权值设为 ;经过预处理的控制网格仍记为
;经过预处理的控制网格仍记为 。
。
最后,进行迭代。先按照非均匀Catmull-Clark细分模式计算出控制网格 内部的新点,以任意方式计算出边界边对应的新边点和边界点对应的新顶点,并将所有新点连成新的拓扑网格,再删除最外一层控制网格。
内部的新点,以任意方式计算出边界边对应的新边点和边界点对应的新顶点,并将所有新点连成新的拓扑网格,再删除最外一层控制网格。
图3是对三张 三次非均匀B样条开曲面进行拼接的结果,其中图3(a)为待拼接的非均匀三次B样条曲面片及其控制网格,图中红色的部分为非均匀Catmull-Clark曲面的初始控制网格。细分6次后,细分曲面对基曲面片的拼接效果如图3(b)和图3(c)所示。图4给出了5张基曲面混合的结果。
三次非均匀B样条开曲面进行拼接的结果,其中图3(a)为待拼接的非均匀三次B样条曲面片及其控制网格,图中红色的部分为非均匀Catmull-Clark曲面的初始控制网格。细分6次后,细分曲面对基曲面片的拼接效果如图3(b)和图3(c)所示。图4给出了5张基曲面混合的结果。


 (a) (b) (c)
(a) (b) (c)
Figure 3. (a) Base surfaces and subdivision control mesh; (b) Base surfaces with any node vectors; (c) The average node distance as the control vertex distance
图3. (a) 基曲面片和细分控制网;(b) 基曲面片节点向量任意指定;(c) 节点距为控制顶点距的平均

Figure 4. Blending of five base surfaces
图4. 五张基曲面片混合
3.2. 插值于N边洞边界曲线的非均匀Catmull-Clark细分曲面
对于N片非均匀双三次B样条曲面片围成N边洞,本文采用插值于角点的非均匀B样条曲面,只需相邻曲面片有公共角点即可。将插值于角点的曲线细分公式统一成轮廓删除模式,根据非均匀Catmull-Clark细分模式的新点计算公式(1),(2),(3),可以证明当最外两层控制网格正则,各行列首尾两条边的权值为零且所有的延伸边权值也为零时,非均匀Catmull-Clark细分模式产生的次外一层控制顶点即为新的控制顶点,且细分后的权值保持初始控制网格权值的特点. 对于N边洞问题本文给出以下算法。
算法1:(形成插值于角点的N边域曲面)。
Step 1:构造细分填充曲面的初始控制网格。保留边界曲线的控制顶点作为细分填充曲面的最外一层控制顶点。为了保证细分曲面的初始控制网格的最外两层顶点正则,当N边洞各边上的独立控制顶点数为奇数时,不再增加中心点,而是相对于各边的中心控制顶点各增加一个新点,再把新点与每个基曲面控制网的第1行中点相连,如图5所示。由于只需满足插值条件,中间的新控制顶点均可任意指定.
Step 2:将初始控制网格向外扩充一层,将所有的延伸边权值都赋为零,采用预处理方法对最外两层正则网格及其邻边边赋权值,延伸后的控制网格记为 。
。
Step 3:第k步迭代时,1) 按照非均匀Catmull-Clark细分模式对赋权的细分控制网格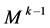 进行细分,生成新的控制网格
进行细分,生成新的控制网格 ;2) 删除最外一层控制顶点,与最外层控制顶点相连的边不进行删除,作为新控制网格的相应延伸边,将其权值作为延伸边的权值.生成的新的带延伸边的控制网格记为
;2) 删除最外一层控制顶点,与最外层控制顶点相连的边不进行删除,作为新控制网格的相应延伸边,将其权值作为延伸边的权值.生成的新的带延伸边的控制网格记为 。
。
图6和图7是对非均匀三次B样条曲线围成的三边洞和五边洞进行连续填充的效果图,红色和蓝色分别为构成N边洞的非均匀三次B样条曲线及其控制网格.通过移动新增加的控制顶点,图6(a)和图6(b)分别生成了凸起的和凹陷的两张曲面。
算法1将插值于角点的非均匀Catmull-Clark细分曲面统一成轮廓删除模式,跟文献[11] 的插值于角点的N边域曲面比起来,对初始控制网格的要求更低,且避免了将初始控制网格分成两个单独的部分来处理,提高了可执行性。
3.3. 基于非均匀Catmull-Clark细分模式的N边洞G1填充
由非均匀Catmull-Clark模式的局部B样条曲面性质,再根据插值于角点的B样条曲面的G1拼接条件,以 为例子给出基于非均匀Catmull-Clark细分模式的N边洞G1填充算法如下。
为例子给出基于非均匀Catmull-Clark细分模式的N边洞G1填充算法如下。
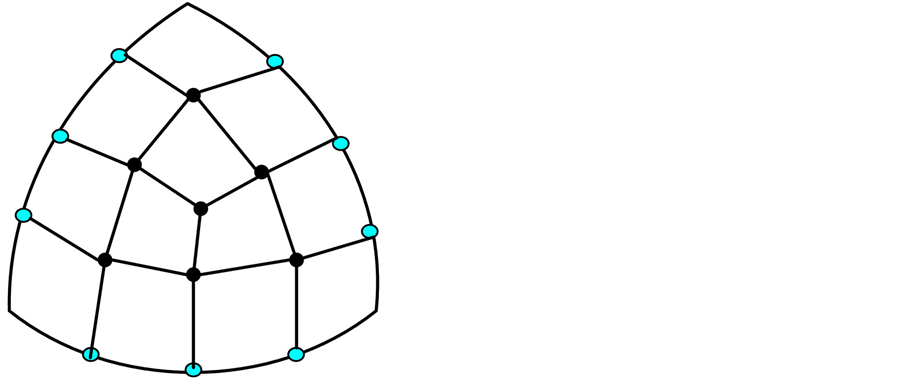
Figure 5. Initial control mesh of filled surface
图5. 填充曲面初始控制网格

 (a) (b)
(a) (b)
Figure 6. (a) Fill convex surface (three-sided hole); (b) Fill concave surface (three-sided hole)
图6. (a) 凸起的填充曲面(三边洞);(b) 凹陷的填充曲面(三边洞)

Figure 7. Fill surface (five-sided hole)
图7. 填充曲面(五边洞)
算法2:(G1填充算法)。
Step 1:构造细分填充曲面的初始控制网格,保留边界曲线的控制顶点作为细分填充曲面的最外一层控制顶点。相对于边界曲面的每一个交界点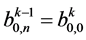 ,对应一个新增控制顶点,记为
,对应一个新增控制顶点,记为 。相对于第
。相对于第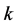 个基曲面片的边界曲线
个基曲面片的边界曲线 中间
中间 个控制顶点,各对应一个新控制顶点
个控制顶点,各对应一个新控制顶点 。
。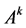 和
和 组成了新增控制点的最外层,也就是细分填充曲面控制网格的次外层.再按照上述规则在内部插入控制顶点(如图8~图10所示)。
组成了新增控制点的最外层,也就是细分填充曲面控制网格的次外层.再按照上述规则在内部插入控制顶点(如图8~图10所示)。
Step 2:确定 和
和 的位置。
的位置。
1) 位于面
位于面 上,且根据下列相容性条件求出:
上,且根据下列相容性条件求出:
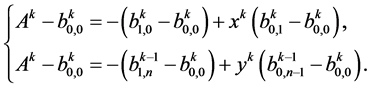
 五点共面保证了上面的相容性条件求解得到唯一的
五点共面保证了上面的相容性条件求解得到唯一的 。
。
2) 同理,根据 的相容性条件可求出
的相容性条件可求出 ,令
,令 ,
, 。
。
3) 对已有的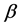 ,
,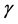 ,根据相邻两Bézier曲面片的G1拼接条件求出
,根据相邻两Bézier曲面片的G1拼接条件求出 的位置。
的位置。
Step 3:对控制多边形的各边赋权值,再用非均匀Catmull-Clark细分方法的轮廓删除模式进行细分迭代。
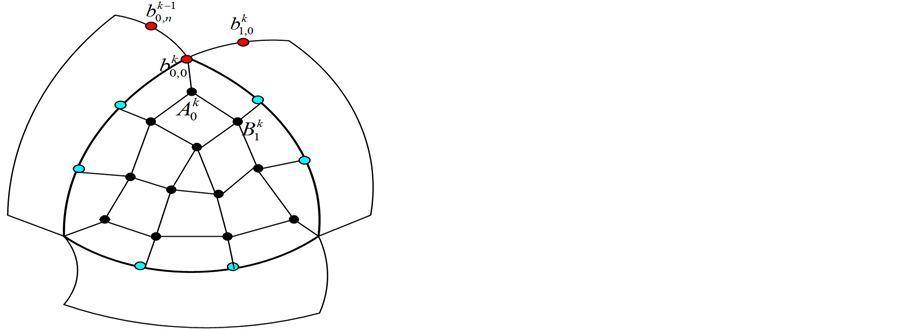
Figure 8. Fill the initial control mesh surface
图8. G1填充曲面的初始控制网格

 (a) (b)
(a) (b)
Figure 9. (a) Base surfaces with three-sided hole; (b) Filling three-sided hole with G1
图9. (a) 构成三边洞的基曲面片;(b) 三边洞G1连续填充
4. 结论
本文研究了Catmull-Clark细分曲面与NURBS曲面的融合。在用非均匀Catmull-Clark细分方法的轮廓删除模式构造N边曲面片的基础上,为NURBS曲面的混合和N边洞填充给出了具体算法。同时,还提出了用非均匀Catmull-Clark细分模式构造N边曲面片的角点插值法,通过改变边界附近的边所对应的参数,把角点插值法归入了非均匀Catmull-Clark细分方法的轮廓删除模式,并由此给出了N边洞的一个填充算法,填充曲面和基曲面G1拼接。本文给出的算法都已在微机上实现。实验表明,本文的算法简单、有效。
基金项目
中国国家自然科学基金(51175248/E050603),南京航空航天大学基本科研业务费(NZ2013201)。