1. 引言
现代材料物理模拟技术中利用热/力实验模拟装置对小试样进行试验检测,可快速、准确地研究材料在近似于实际情况下的性能和组织的变化规律,因此物体模拟技术在材料工程界受到广泛重视。压力加工作为物理模拟技术在热加工工艺研究中最重要的领域之一,其目的在于通过材料在不同变形条件下热压缩变形获得的不同性能和组织,从而确定最佳的热加工工艺[1] -[3] 。但在圆柱体试样的热压缩过程中,通常由于端面存在较大摩擦力,变形后试样往往会出现上下端面小而中间凸的腰鼓状,即发生不均匀变形。变形的不均匀将直接影响材料的析出动力学与形变再结晶,从而导致相应区域性能与组织特性不均匀 [4] [5] 。因此,深入研究热压缩试样纵剖面上变形不均匀性及其规律,对指导物理模拟实践具有重要意义。
随着计算机技术的迅速发展,诸如DEFORM、ABAQUS、COMSOL Multiphysics等有限元软件在科学研究与工程领域应用越来越广泛,有限元模拟通过将数学方程转化为数字式图象来描述材料变形过程中的物理现象,可有效提高科研效率。通过实验数据与有限元模拟相结合的方式是研究材料热压缩过程中不均匀变形的有效途径 [6] [7] 。
本文通过Gleeble-3800热模拟试验机在变形温度为300℃~500℃、变形速率为0.01~10 s−1、变形量为50%范围内对5083铝合金进行了热压缩实验,以实验数据为基础建立DEFOM-3D有限元模型,通过软件模拟了5083铝合金在变形温度为400℃应变速率为1 s−1,变形温度为400℃应变速率为10 s−1,变形温度为500℃应变速率为1 s−1条件下的热压缩变形过程,利用后处理程序分析了试样不同部位应变场、应变速率场、应力场和温度场的不均匀性特征,为材料物体模拟过程的不均匀性研究提供了参考依据。
2. 实验方法
2.1. 实验材料与物理模拟
实验用材料为已再结晶的5083铝合金板材,板材经机加工成Φ10 × 15 mm的圆柱体试样。在Gleeble- 3800热模拟机上进行等温压缩实验,压缩温度分别为300℃、400℃、500℃,应变速率分别为0.01、0.1、1、10 s−1,变形量为50%,压缩时试样两端添加石墨片并均匀涂上润滑剂(75%石墨 + 20%机油 + 5%硝酸三甲苯脂)以减小摩擦的影响。加热温度为5℃/s,保温2 min。对物理模拟实验数据进行处理,计算出Al-4.5Mg-0.6Mn铝合金材料在变形温度为300℃~500℃、变形速率为0.01~10 s−1、变形量为50%范围内的本构方程为:
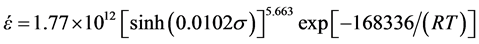
其中έ为变形速率;σ为流变应力;R为摩尔气体常数;T为变形温度。
2.2. 有限元模型的建立
用DEFORM-3D有限元软件建立热压缩变形过程的三维有限元模型,模型如图1所示。模拟试样尺寸与实验试样尺寸保持一致,均为Φ10 × 15 mm,为减少计算量,选取圆柱体试样的1/2进行模拟运算;两端压头材料特征设定为刚性,压缩试样材料选用5083铝合金,材料流变应力本构关系选用上述实测数据所计算出的本构方程;实验过程中一端固定,另一端以恒定应变速率沿Z向变形至50% (真应变0.69);模拟过程中试样整体温度设定为400℃或500℃。
3. 实验结果与分析
3.1. 应变场分布及变化
图2(a)所示为5083铝合金热压缩后的应变分布情况,其中压缩方向为Z向。从图2(a)中可以看出,试样经热压缩后其应变分布明显不均匀。这是由于试样端面和压头之间存在摩擦力,在一定程度上改变了金属的流动特性,从而使得整个变形区分为三个变形区:易变形区、难变形区和自由变形区。其中,热压缩试样中心区域(易变形区)应变值最大,如P1点处,应变值为1.1,而应变设定值为0.7;与压头接触的试样端面中心处(难变形区)应变值最小,如P2点处,其应变值为0.151;试样圆柱面腰鼓处(自由变形区)应变值处于中间,如P3处,应变值为0.552。
对上述三个典型位置的应变值变化情况进行追踪分析,研究其应变值随时间增加的变化情况,结果如图2(b)所示。在热压缩初期,不同区域的应变值增加比较缓慢,各处的应变相差不大,随着变形的增加,P1点处网格畸变最严重,应变值增长速率最快且数值最大,P3点处网格基本变化不大,应变值基本不发生变化,此位置试样未发生明显变形,P2点处应变值增呈线性增长。由此可见,试样热压缩过程中变形非常不均匀。
一般来说,动态再结晶的初始形核与应变量有着密切联系。热变形过程中往往伴随着动态回复和动态再结晶的发生,一方面随变形量的增加使位错不断累积,产生加工硬化,另一方面,通过热激活作用使位错对消及形成亚晶,发生软化作用。在热压缩初期,晶粒内因位错密度小而难以发生动态再结晶,随着变形的增加,当位错累积到一定程度后,就会发生动态再结晶 [8] [9] 。由模拟结果可以看出,压缩变形时P3处应变值一直很小,处于加工硬化状态。随着时间的增加,P2和P1处应变值迅速增大,且P1处在较短时间内即可发生动态再结晶。
如图3所示,图3(a)是在变形条件为400℃,10 s−1时变形50%的应变场分布图,图3(b)是在变形条件为500℃,1 s−1时变形50%的应变场分布图。由图2(a)和图3(a)对比可知,随着应变速率的增加,不均匀变形的程度有所变大,心部应变量由1.1上升到1.17,较预设值0.7由57.14%增加为67.14%。由图2(a)和图3(b)对比可知,随着变形温度的增加,不均匀变形的程度有所变大,心部应变量由1.1上升到1.12,较预设值0.7由57.14%增加为60%。综上所得,应变速率对应变量的影响大于变形温度的影响。
3.2. 应变速率、应力场和温度场分布
热压缩时试样变形的不均匀性导致了试样应变的不均匀,同时也对试样的应变速率、应力及温度场分布产生了不同程度的影响,在变形温度为400℃应变速率为1 s−1条件下结果如图4所示。选取三个典型的位置进行分析,由图4可知,应变速率、应力及温度的不均匀性与应变分布基本一样,均表现为易
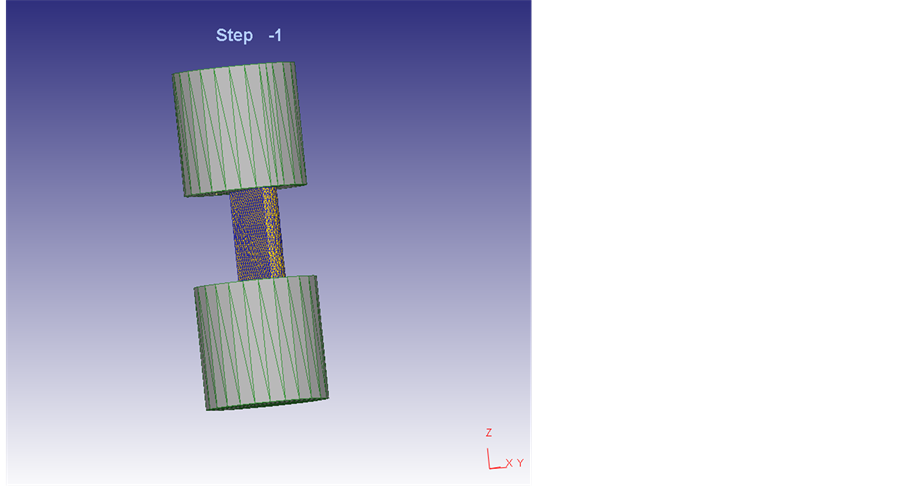
Figure 1. Finite element model of the hot compression sample
图1. 有限元分析模型
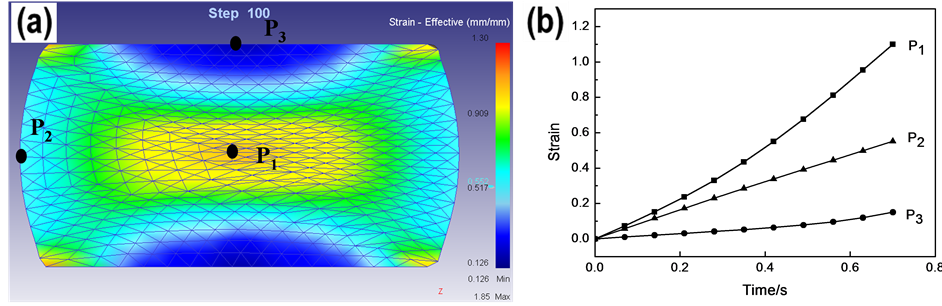
Figure 2. Distribution of strain in simulated sample compressed to strain of 0.7 (a) and change curves of strain with time (b) (400˚C, 1 s−1)
图2. 试样压缩至应变量0.7时的应变分布及随时间的变化曲线(400℃,1 s−1)

Figure 3. Strain distribution under different deformation conditions: (a) 400˚C, 10 s−1; (b) 500˚C, 1 s−1
图3. 不同变形条件下应变分布:(a) 400˚C,10 s−1;(b) 500˚C,1 s−1

Figure 4. Distribution of strain rate, stress and temperature in simulated sample compressed to strain of 0.7 and change curves of strain with time (400˚C, 1 s−1): (a) Distribution of strain rate; (b) Distribution of stress; (c) Distribution of temperature; (d) Detail values for three typical points in compressed sample
图4. 试样压缩至应变量0.7时的应变速率、应力及温度分布及随时间的变化曲线(400℃,1 s−1):(a) 应变速率分布;(b) 应力分布;(c) 温度分布;(d) 试样不同位置的变形参数
变形区P1处的对应值最大,难变形区P3处的对应值最小,具体数据如图4(d)所示。
值得注意的是,热压缩时的变形温度实际为422℃~424℃,而实验预设温度为400℃。这是因为热压缩变形时塑性变形所消耗的机械能大部分转化为热能,而当应变速率较高时(έ ≥ 1 s−1),变形时间非常短,使得变形过程中产生的热能来不及散失,使试样温度瞬时剧升。由此可得,试样的中心区域是在高温高速状态下进行压缩变形的,对其再结晶晶粒尺寸的预测不能严格按初始变形条件进行预测。为了合理预测再结晶晶粒尺寸,需对实验数据进行修正 [10] 。
4. 结论
1) 5083铝合金热压缩过程具有明显的变形不均匀性,试样变形区可分为易变形区、难变形区和自由变形区三个区域。
2) 5083铝合金热压缩时试样的中心区域是在高温高速状态下进行压缩变形的,对其再结晶晶粒尺寸的预测不能严格按初始变形条件进行预测,为了合理预测再结晶晶粒尺寸,需对实验数据进行修正。
3) 随着应变速率和变形温度的增加,不均匀变形的程度有所变大,但应变速率对不均匀变形的影响大于变形温度的影响。
基金项目
广西科技计划项目(编号:桂科重14122001-5、1598001-2)。