1. 引言
基于数据的机器学习是现代智能技术中的重要方面，它是从观测数据出发寻找规律，并利用这些规律对不方便直接观测的数据进行预测[1] 。核Fisher判别方法就是基于Fisher线性判别提出的一种非线性分类方法[1] 。随着社会和科学技术的发展，电磁环境越来越复杂，无线电通信面临的干扰问题也日益严重。本文尝试将核Fisher判别方法应用在数字通信领域，并用MATLAB对其进行了仿真和分析，取得了较好的检测识别效果，提高了数字通信的抗干扰能力。
2. 核Fisher判别方法基本原理
核Fisher判别方法由Mika等人于1999年提出[2] 。假设有一集合X包含n个d维数据
，其中
个属于
类的样本记为
，
个属于
类的数据记为
。
Fisher 线性判别所要解决的最基本问题是找到一个最好的投影方向，使样本在这个投影方向上能最容易分开。从数学的角度分析，寻找最好投影方向的问题就是寻找最好的变换向量
的问题，即最大化下列广义Rayleigh熵[3] ：
(1)
式中
上述两式分别是样本的类间离散度矩阵和类内离散度矩阵，而
是各类样本的均值向量
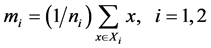(2)
因此最大化
的本质是要找到一个最好的投影方向来最大化类间离散度，同时最小化这个方向上的类内离散度。
对于非线性分类[3] ，首先就是用一个非线性映射函数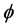
，把数据从原始空间F映射到一个特征空间H (图1)，再在特征空间H建立一个优化超平面。特征空间H的维数有时非常高，而核函数则利用点积运算解决了这个问题。例如，常用的RBF核函数为：
核Fisher判别方法首先把数据非线性地映射到某个特征空间，然后在这个特征空间中进行Fisher线性判别，这样就间接地实现了对原始输入空间的非线性判别。假设
是输入空间到某个特征空间H的非线性映射。要找到H中的线性判别就需要最大化
Figure 1. Mapping from the sample space to feature space
图1. 从样本空间到特征空间的映射
(3)
这里
，
和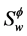
是H中的相应矩阵，即
(4)
(5)
其中
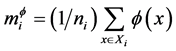(6)
如果H的维数很高，那么直接求解就不可能。核Fisher判别方法不需要对数据进行明确的映射，而是寻找一种算法的表达式，其中只使用了训练数据的点积运算。然后只要能够有效地计算这些点积，就能够解决原始的问题。
为了找到特征空间H的Fisher判别，首先需要得到按照输入样本数据的点积形式表示(1)的表达式，然后用一个核函数来替代其中的点积运算。依据再生核理论，任何
必位于所有训练样本在H的张集中，因此可以找到下列形式的w的一个展开表达式
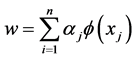(7)
利用展开表达式(7)和(6)，并用核函数代替点积，于是有
(8)
式中定义：
再来考虑式(1)中的分子。利用
的定义式(4)和式(8)，它可重写为
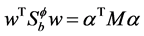(9)
再来考虑式(1)中的分母。利用式(7)，(5)及式(9)中类似的变换，得到
(10)
式中
其中
是第j类的核矩阵
I为单位矩阵，
是所有元素为
的矩阵。
把式(9)和(10)代入式(4)，可得到特征空间H的Fisher线性判别，也就是最大化
(11)
和输入空间的算法类似，求解该问题可以通过求矩阵
的特征值和特征矢量，或者计算
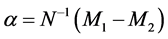来得到。则新模式x到w的投影为
(12)
由上可知，这个设置是非适定的。因为要从n个样本中估计n维的协方差结构，而特征空间的维数等于或高于训练样本数目n，这时就要利用正则化技术。可以给N加上一个单位矩阵的倍数，即用矩阵
代替矩阵N，
(13)
来补偿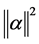
，或者给N加上一个全核矩阵
的倍数来补偿
。
3. 仿真结果及结论
在本实验中，模拟的是点对点数字通信系统。具体过程如下：用随机函数模仿用户发送的信号，信号加上多径迟延和进入信道后的加性噪声，就是从信道出来的数字信号，然后对该信号分别用核Fisher判别方法和匹配滤波方法对其检测识别，计算正确识别率。本实验方法如下：
数据训练样本长度为100，检测样本数据长度为10,000；信噪比(S/N)从1 dB到10 dB的逐渐增强；在这里我们用RBF核，并且核参数为经验值。
表1中所示为在不同信噪比条件下核Fisher判别方法与匹配滤波方法的识别率比较：在信噪比从1 dB
Table 1. Comparison of different S/N (dB) detection and recognition rate
表1. 不同S/N(dB)检测识别率比较
到10 dB的过程中，核Fisher判别的检测识别率从0.852上升到0.971，同时匹配滤波则是从0.806升到0.966。
通过对以上数据的分析可以看出，基于RBF核的Fisher判别方法在数字通信中相对于匹配滤波有较好的识别效果，这是由于道干扰不是完全随机，通过学习机的学习过程之后，识别效果有明显的改观，提高了抗干扰能力。随着数字通信面临的抗干扰压力越来越大，核Fisher判别分析方法在数字通信中将有较大的应用潜力。