1. 前言
叠合梁被广泛应用于实际工程中,如吊车梁、汽车板簧等。孙振东 [1] 通过将两根同种材料的两端简支叠合梁进行实验研究,在一般受力情况下,不能将各层梁简化为相同的力学模型,只有纯弯情况下可以简化为相同的力学模型。吴晓 [2] 推导出两端简支条件下无销钉和有销钉连接叠层梁的弯曲正应力公式。徐慧 [3] 从理论分析与实验计算两方面验证了在两端简支条件下两根截面相同,材料不同的组合梁数值计算方法及其应力分布的正确性。然而针对两端固支条件下两种不同材料叠合梁的应力分析尚未有相关报道。因此,开展两端固支叠合梁在一般受力条件下的弯曲正应力分布研究十分必要,对于推动和发展该类梁的分析计算理论具有极为重要的工程应用价值。
本文采用电测技术对钢铝两种材料组成的自由和完全两端固支叠合梁进行了实测研究,分别得到了其跨中与近固端截面各测点的弯曲正应力实测数据,根据已有文献给出了弯曲正应力的计算公式,最后对这两种叠合梁弯曲正应力的理论计算值和电测值进行了对比分析。
2. 实验模型与固支约束构件
本实验所用的两端固支自由和完全叠合矩形截面梁的实验模型分别见图1和图2。这两种叠合梁是由上铝、下钢两种材料通过自由和完全叠合方式而成的,其材料参数和几何参数见表1。应变片粘贴在如图1和图2所示的跨中2-2和近固端1-1 (离左端距离为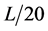 )横截面上,并且在这两个截面上均黏贴了16片电阻应变片,它们的位置如图3所示。为了实现两端固支约束条件,本试验自制了图4所示的固端约束构件及与试验台连接方式。
)横截面上,并且在这两个截面上均黏贴了16片电阻应变片,它们的位置如图3所示。为了实现两端固支约束条件,本试验自制了图4所示的固端约束构件及与试验台连接方式。
3. 电测应力分布
3.1. 电测方案
本实验将原梁弯曲正应力试验台的简支端替换成如图4所示的固支约束构件,即可改装为两端固支叠梁弯曲正应力测定的试验台。采用1/4桥路连接方式,应变数据的采集采用XL2118C型电阻应变仪。运用等增量法加载方式,共5级,每级荷载增量为 ,最大荷载为
,最大荷载为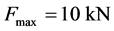 。
。
3.2. 自由叠合梁应力分析
根据上述试验方案和电测技术,首先获得五个不同等级载荷下两端固支自由叠合梁跨中和近固端两个截面上的各测点应变值,然而利用胡克定律便得到相应的各测点弯曲正应力值,其结果见表2、图5和图6所示。
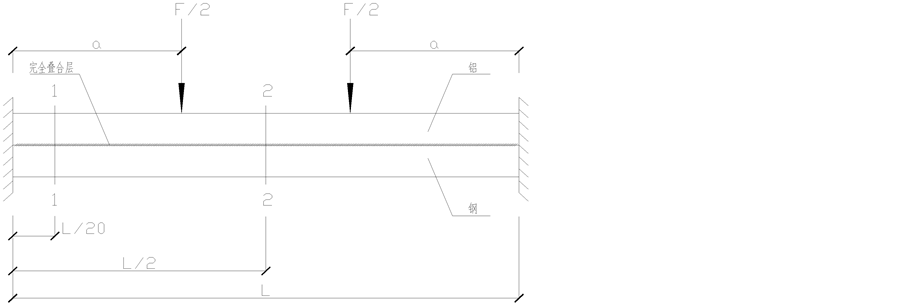
Figure 2. Completely bonded laminated beam
图2. 完全叠合梁

Table 1. Material and geometric parameters of a laminated beam
表1. 叠合梁的材料和几何参数
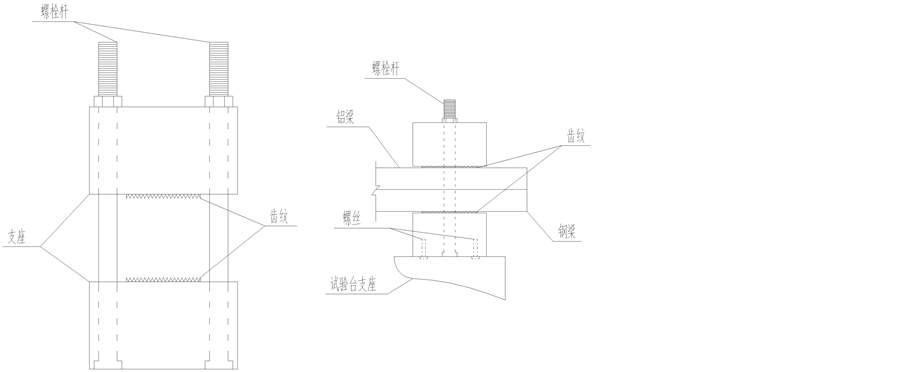
Figure 4. Sketch and bonding type of constraint components at two fixed ends
图4. 固端约束构件草图及连接方式

Figure 5. Distribution of axial stress at a mid-span for a free laminated beam
图5. 自由叠合梁跨中截面应力分布图
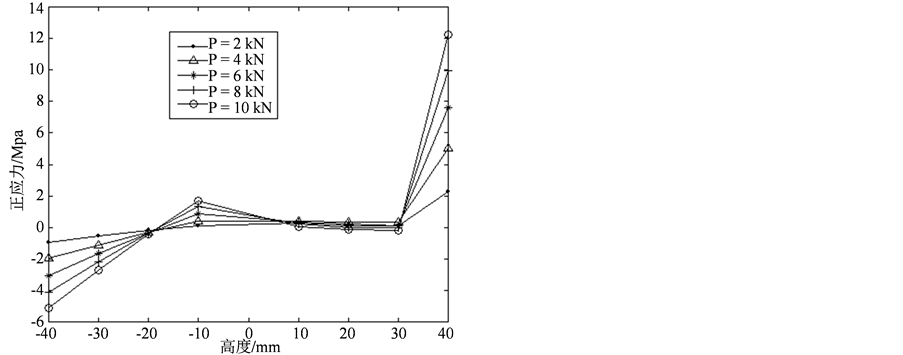
Figure 6. Distribution of axial stress at a section nearby the fixed end for a free laminated beam
图6. 自由叠合梁近固端截面应力分布图

Table 2. Measuring values of stress at a mid-span and a section nearby the fixed end for a free laminated beam (Mpa)
表2. 自由叠合梁跨中及近固端截面各测点应力值(Mpa)
由图5可知自由叠合跨中截面上的应力分布特点:1) 上、下梁可近似看做单独工作,每层梁均有各自的中性层;2) 跨中截面上的弯曲正应力沿高度方向按分段线性分布;3) 上、下梁交界处存在着应力突变。
由图6可知自由叠合近固端截面上的应力分布特点:1) 上、下梁中性层到外边缘这段区间,近固端截面上的弯曲正应力沿高度方向仍按分段线性分布。2) 上、下梁中性层之间的区间两梁协同工作,应力变化不明显,但随着外荷载的增加,这种协同效果逐渐减弱。
3.3. 完全叠合梁应力分析
根据上述试验方案和电测技术,首先获得五个不同等级载荷下两端固支完全叠合梁跨中和近固端截面上的各测点应变值,然而利用胡克定律便得到相应的各测点弯曲正应力值,其结果见表3、图5和图6所示。
由图7可知完全叠合梁跨中截面应力分布规律:上下梁共同工作,变形协调,中性层在下层钢梁中,上层铝梁全截面受压,下层钢梁沿高度方向成线性分布。
由图8可知完全叠合梁跨中截面应力分布规律:中性层上移,但具体位置由于测点布置数量较少而难以确定。叠梁在近固端截面的应力分布类似于整梁的应力分布规律,沿高度方向大致曲线分布。
4. 叠合梁弯曲应力计算公式
4.1. 自由叠合梁弯曲应力
两端固支自由叠合梁的理论分析模型如图9所示,其弯曲正应力计算公式可参照文献 [2] [4] - [6] 。任一截面上、下梁的最大弯曲正应力计算公式 [2] 为:
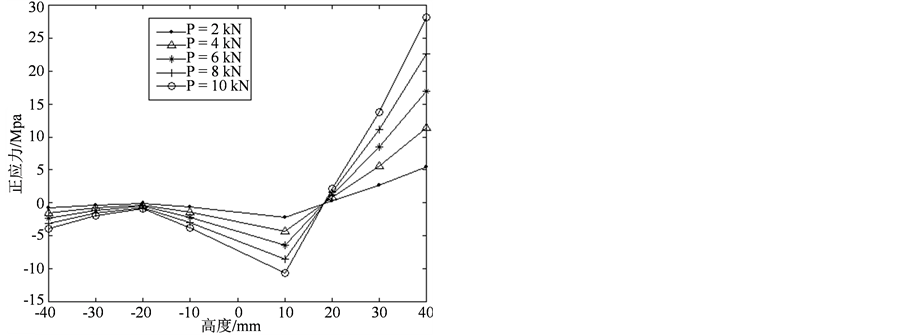
Figure 7. Distribution of axial stress at a mid-span for a completely bonded laminated beam
图7. 完全叠合梁跨中截面应力分布图
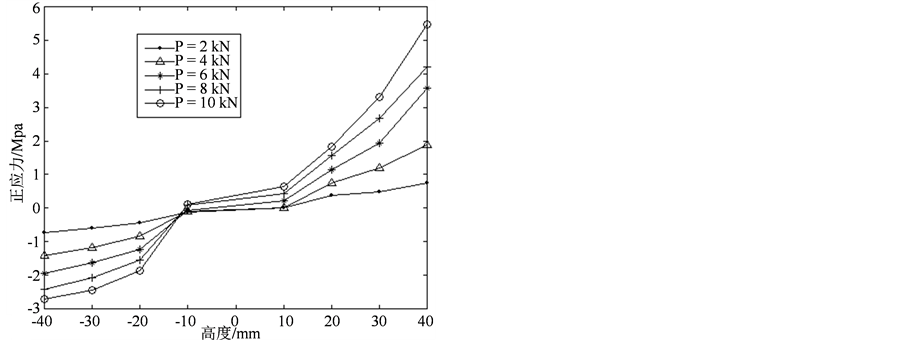
Figure 8. Distribution of axial stress at nearby the fixed end for a completely bonded laminated beam
图8. 完全叠合梁近固端截面应力分布图
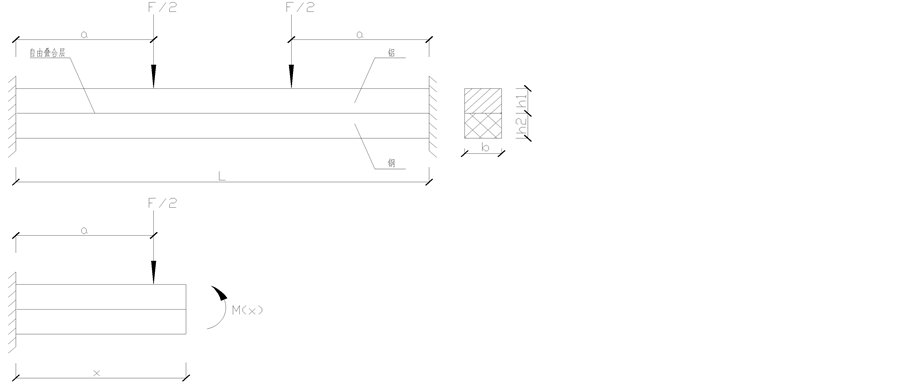
Figure 9. Computational model of a free laminated beam
图9. 自由叠合梁

Table 3. Measuring values of stress at a mid-span and a section nearby the fixed end for a completely bonded laminated beam (Mpa)
表3. 完全叠合梁跨中及近固端截面各测点应力值(Mpa)
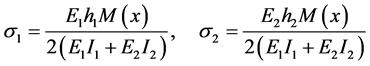 (1)
(1)
[7] 利用变形协调条件和结构力学理论,易求得支座反力,从而得如式(2)的弯矩方程:
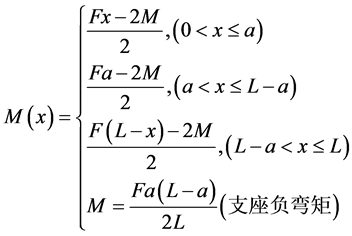 (2)
(2)
当 ,即
,即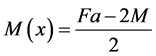 。当
。当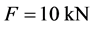 时,
时,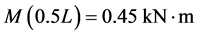 ,将
,将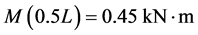 代入(1)式,可得钢梁及铝梁在跨中处的最大弯曲正应力分别为
代入(1)式,可得钢梁及铝梁在跨中处的最大弯曲正应力分别为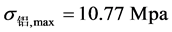 和
和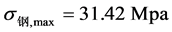 ,
,
理论计算值与实测值之间的相对误差分别为9.38%和2.58%。由此可见,考虑到外界因素影响以及电阻应变仪本身的系统误差的影响,理论值与实验值之间的误差是较小的,可以接受的,故(2)式对两端固支自由叠合梁跨中截面的最大弯曲正应力理论计算是适用的。
4.2. 完全叠合梁弯曲应力
根据文献 [2] ,两端固支完全叠合梁的理论分析模型如图10所示。假设忽略上下梁之间的滑移,在外
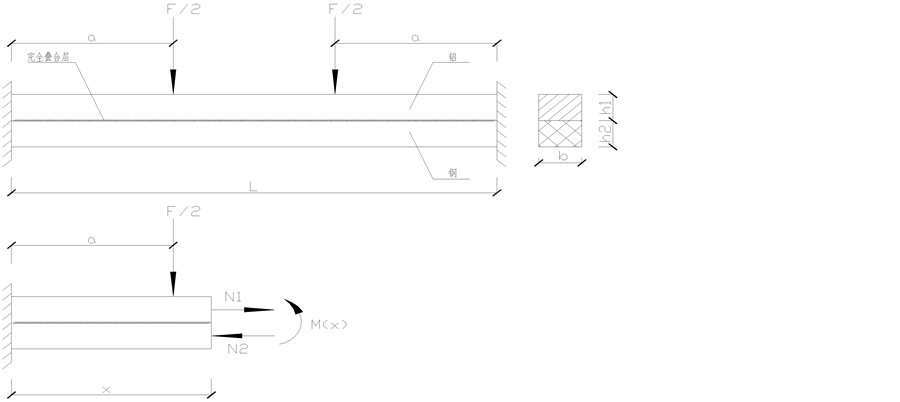
Figure 10. Computational model of a completely bonded laminated beam
图10. 完全叠合梁
荷载作用下叠梁发生弯曲变形,上下梁共同工作,中性层存在于刚度较大的材料中,上下梁都存在轴向力 、
、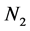 ,且满足下式:
,且满足下式:
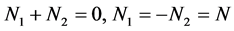 (3)
(3)
由图10可知叠合梁任一截面的弯矩应满足以下条件:
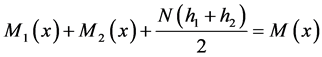 (4)
(4)
为求得轴向力 及弯矩
及弯矩 、
、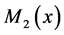 需引入变形协调条件,即上梁下表面及下梁上表面的应变相等。整理可得:
需引入变形协调条件,即上梁下表面及下梁上表面的应变相等。整理可得:
 (5)
(5)
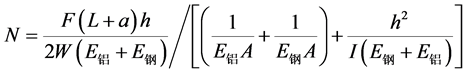 (6)
(6)
以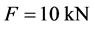 为例,代入数据得
为例,代入数据得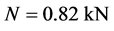 ,
,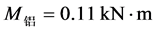 ,
, ,假设上下梁独立工作,将数据代入(1)式得跨中的最大弯曲应力分别为
,假设上下梁独立工作,将数据代入(1)式得跨中的最大弯曲应力分别为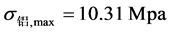 和
和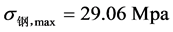 ;假设上下梁协同工作(即叠梁只有一个中性层),经中性层位置修正可得跨中最大弯曲应力
;假设上下梁协同工作(即叠梁只有一个中性层),经中性层位置修正可得跨中最大弯曲应力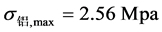 和
和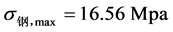 。结合两种情况可得上下梁最大弯曲应力的范围分别为:
。结合两种情况可得上下梁最大弯曲应力的范围分别为: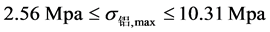 和
和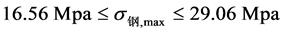 。由表3可知完全叠合梁实测值分别为
。由表3可知完全叠合梁实测值分别为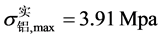 和
和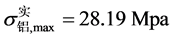 ,恰落在理论计算结果范围内。故公式可以用于估算叠梁承载力,但最终结果以实验数据为准。
,恰落在理论计算结果范围内。故公式可以用于估算叠梁承载力,但最终结果以实验数据为准。
5. 结语
本文针对钢–铝两种不同材料组合而成的自由叠合梁和完全叠合梁在两端固支约束下,对其跨中与近固端截面上弯曲正应力的分布进行了电测实验研究。基于合理的假定基础上,提出了两种叠合梁的简化模型,推导了两种梁的正应力计算公式,将理论分析与电测结果进行了比较。研究结果表明:由于实验模型叠合的紧密程度以及纯弯梁试验台反力架刚度与理论假设存在偏差,造成了理论值与实验值之间的偏差,然而该误差能够控制在工程应用范围内,故本文的计算公式适用于两端固支叠梁的弯曲正应力估算。
基金项目
2015年浙江省大学生科技创新活动计划暨新苗计划(No. 2015R417013)。