1. 引言
复杂网络作为一门交叉学科，涉及数学、力学、物理学、计算科学、管理科学、系统科学、社会科学、金融经济科学等许多领域，在最近十几年里受到学者的广泛关注与研究 [1] - [6] 。复杂网络的研究工作从18世纪欧拉开创的图论开始，到20世纪60年代Erdos和Renyi创立随机图理论，即随机网络模型 [7] ，已经取得了很大的进步。研究表明随机网络的度分布是泊松分布，平均度与节点总数N成正比，平均集群系数与N成反比，平均距离与lnN成正比。但是现实世界中的绝大多数网络并不是完全随机的，直到1998年Watts和Strogatz发表了一篇有关小世界网络的文章 [8] ，实现了从完全规则网络到完全随机网络的转变。同时发现小世界网络具有与规则网络类似的高聚类性，又具有与随机网络类似的小平均路径长度；还有1999年Barabasi和Albert发表了有关无标度网络研究的文章 [9] ，并指出许多实际复杂网络的度分布具有幂律形式，没有明显的特征长度，少数节点的度很大，大多数节点的度较小，即无标度特性。这两篇标志性文章的发表，更是将复杂网络的研究推向了新的高潮。
复杂网络的模型构建基于图论的思想，具有八次旋转对称性的Ammann-Beenker (AB)拼图 [10] ，作为准周期结构的一种典型模型，不但具有周期结构的规则性，而且具有分形图的自相似性。将其作为复杂网络的基本模型，或在此规则模型的基础上演化出带有一定随机成份的网络模型，研究其统计性质，是一个有意义的工作。我们分别考虑网络中节点间的边连接方式与距离平方有关和度值种类有关，理论分析和数值模拟结果表明，由规则AB拼图网络得到的演化网络具有随机网络的统计性质，还具有层次拓扑结构。本文的研究工作是准周期结构在复杂网络研究中的一次有意义的尝试，为认识准周期结构的丰富性质打下了基础。
2. 规则AB拼图网络模型的统计性质
二维准晶体结构中用的最多的几何模型是彭罗斯拼图，由两种基本单元构成，一种是锐角为72度的胖菱形，另一种是锐角为36度的瘦菱形。类似地，AB拼图也可以由两种基本单元拼砌而成，一个正方形和一个锐角为45度的菱形。自相似变换规则如图1(a)，经过二次变换后得到的结构如图1(b)。
将AB拼图的顶点看作网络的节点，节点间通过菱形或正方形边直接相连，不考虑箭头的方向，则为规则的无向复杂网络。首先计算网络节点的度分布。由于图形的规则性，此理想网络内部的节点有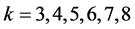
这六种度值。若考虑到有限大小图形的边界效应，则还会有k = 2的节点。在这样的规则网络中，度分布是离散的，即有七个独立的峰值，计算结果如图2所示。所考虑的网络是由包含16个节点的AB拼图开始，经过三次自相似变换，依次得到的包含80，432，2436个节点的图形。从中可以看
(a)
(b)
Figure 1. (a) The self-similar transformations of a square and a rhombus for generating AB tiling; (b) a patch of AB tiling obtained after twice self-similar transformations starting from a rhombus.
图1. (a) 产生AB拼图的正方形-菱形自相似变换法则；(b) 从一个菱形拼块开始，经过2次自相似变换过程后生成的AB拼图
Figure 2. Degree distribution of the regular AB patterns
图2. 规则AB拼图网络的度分布
到，度为k = 3的节点所占比例最大。
集群系数描述网络中节点的邻点之间也互为邻点的关系，该系数可体现小集团结构的完美程度。网络的集群系数定义为
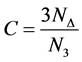
其中
表示网络中三角形的总数，
表示网络中“三元组”(即缺少一边的三角形)的总数，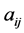
表示网络邻接矩阵的矩阵元。若两个节点i和j直接相连，则aij =1，否则aij = 0。由于AB拼图网络中只有正方形和菱形两种基本单元，不存在三角形，所以根据集群系数C的定义，该规则网络的集群系数C = 0。
网络的度相关性可定义为
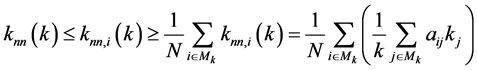
其中Ni表示节点i的邻点集合，Mk表示度为k的节点集合，
表示网络邻接矩阵的矩阵元。如果
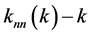曲线的斜率大于零，称为度正相关；
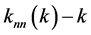曲线的斜率小于零，称为度负相关；
曲线的斜率等于零，称为度不相关。
数值模拟表明该网络模型中既存在部分正相关又存在部分负相关，如图3所示。这使得整个网络的度值比较均衡，既不会像正相关那样出现度值大的节点很多而度值小的点很少的情况，也不会像负相关那样出现度值大的点很少而度值少的点很多的情况。
3. 演化AB拼图复杂网络模型的统计性质
规则的AB拼图网络比较简单，所得的统计性质也比较单一。下面我们在规则的AB拼图网络上以一定概率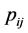
随机加边，演化出具有一定的随机成分的复杂网络。设任意两节点间的连边概率
与节点间距离的平方成反比，即
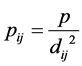，其中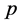
为可调的概率常量。我们计算了节点总数N = 14000，在不同连接概率p的情况下的度分布，结果如图4所示。拟合结果显示，图形都近似为围绕平均度
的泊松分布。当连接概率p增大时，度分布的范围变宽，即网络中的度值种类增加，整个网络的平均度也增加。
对于集群系数的计算可发现，在连接概率一定时，网络的集群系数随着节点总数的增加而减少，而当固定节点总数时，集群系数则随着连接概率的增加而增加，如图5所示。
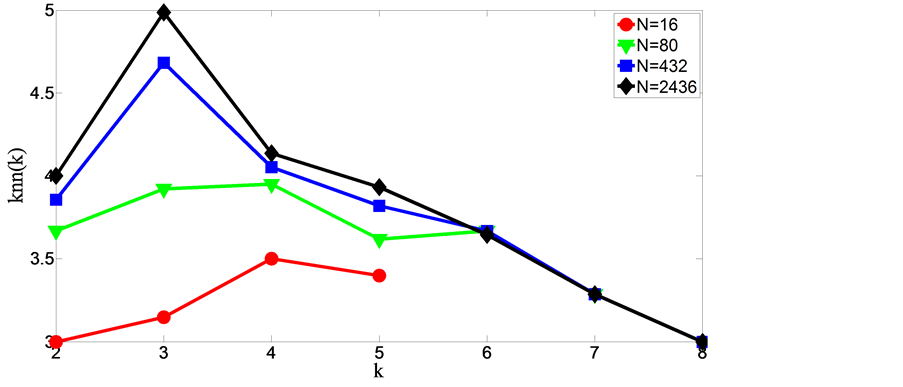
Figure 3. Degree correlations of the regular AB network
图3. 规则AB拼图网络的度相关性
Figure 4. Degree distribution of the complex networks with number of nodes N=14,000 evolved by different connection probability
图4. 节点总数N = 14,000时在不同连接概率下的度分布图
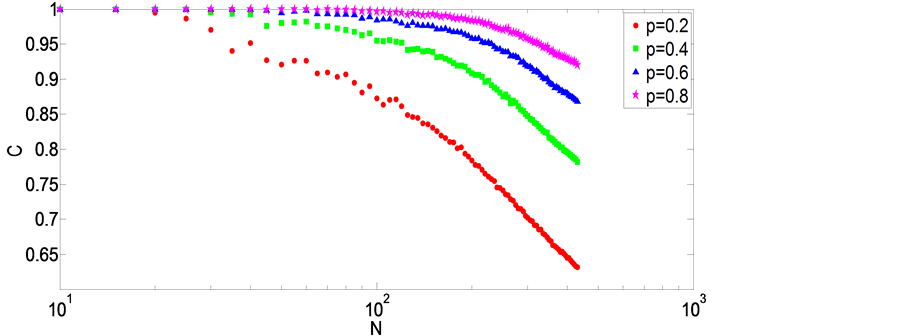
Figure 5. Cluster coefficient versus total number of nodes for networks evolved from different connection probability
图5. 集群系数在不同连接概率下随节点总数的变化关系
4. 结论
本文从准晶结构中具有八次对称性的AB拼图出发，结合复杂网络理论，研究了规则AB拼图网络以及在此基础上演化的网络模型的统计性质。对于规则AB拼图网络，由于度值只有固定的几种，度分布图是散点图。从度相关性方面可看出网络整体上是比较均匀的。该规则模型中只存在正方形和菱形两种基本单元，不存在三角形，故集群系数为0。演化模型是在规则AB拼图的基础上添加随机连接而得到的。研究发现该网络的度分布近似为泊松分布，当网络节点总数固定，改变连接概率时，泊松分布图形逐渐展宽。由准周期拼图构造出的复杂网络具有一些独特的统计性质，并可用于模拟现实中的某些网络，丰富了复杂网络的研究。