1. 引言
对信号稀疏度的估计一直是稀疏表示领域中需要迫切解决的问题,当我们知道了信号稀疏度时,可以更为准确的对信号进行稀疏表示。目前对信号的稀疏度估计的方法有主成分变换(Principle Component Analysis, PCA)方法 [1] - [3] 、自适应稀疏度估计的贪婪回溯(Adaptive Sparsity Matching Pursuit, ASMP)方法 [2] [4] [5] 等是目前比较常用的方法。
前者通过类似小波变换方法估计图像稀疏度的方法设计出利用主成分分析变换来估计图像稀疏度,主成分变换方法表示具有速度快、复杂度低等优点,因此利用主成份分析方法进行稀疏度估计的结果评价更客观。文章假设图像的稀疏度与其方差存在线性关系,且该线性关系可以通过数据拟合得到,在仿真中利用主成份分析方法计算图像的方差,利用拟合得到的线性关系估计图像的稀疏度,仿真测试结果显示这种方法取得了很好的稀疏度估计效果。但该方法依然存在不足,一是没有充分的理论依据对文中的假设做出说明,二是仿真测试选择的图像数量过少。
后者是通过采取一种新的稀疏表示匹配算法ASMP算法,迎合自然条件下稀疏度未知的条件,弥补文中算法的不足,该算法不仅互补了MP,OMP等匹配算法中的缺陷,在算法复杂度及鲁棒性方面都有所增强。同时在图像的稀疏分解中,综合StOMP算法和CoSaMP算法的优势,互补了以上两种算法的缺陷,在提高算法鲁棒性和可靠性的同时折中了传统稀疏分解去噪算法的时间开销。
以上两种方法主要应用于图像处理领域。但在一维信号处理领域,对信号稀疏度的估计的要求和图像压缩不同。本文尝试通过探求信号中的噪声特性,根据噪声的分布特性,在遍历信号在全频域的的稀疏特性的基础上,构造一种估计信号稀疏度的方法。利用信号在冗余稀疏度的稀疏分解下的相对误差的分布,逐步准确的估计信号在噪声下的稀疏度。并通过仿真数据对提出的方法进行验证。
2. 稀疏基与稀疏表示算法
2.1. 傅立叶基字典的构造
傅立叶变换能够得到信号的频域表示,反映了信号在全部时间范围内的所有频谱成分,因此,傅立叶变换在描述平稳信号时效果很好。如果将傅立叶变换以基的形式描述,则傅立叶基是频域字典中最典型的一个完备字典,这个字典的原子可用正弦波性的集合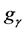 表示,如式(1)所示,
表示,如式(1)所示,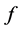 表示原子的频率,
表示原子的频率,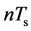 表示信号时间 [6] [7] 。
表示信号时间 [6] [7] 。
 (1)
(1)
其中 。
。
2.2. 正交匹配追踪算法
正交匹配追踪算法在稀疏分解中的应用最广泛,它的原理是在一般匹配追踪的基础上增加正交化过程,这个过程可以用更少的原子来表示信号,使信号变得更为稀疏,因此OMP算法的收敛速度较快 [8] 。
OMP算法用于信号的稀疏表示的具体步骤如下:
步骤1:设定算法输入,信号y,字典A,稀疏度K。
步骤2:初始化算法参数,残差 ,分解系数
,分解系数 ,索引集
,索引集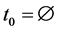 ,子字典
,子字典 ,迭代因子
,迭代因子 ,最大迭代次数
,最大迭代次数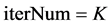 。
。
步骤3:迭代过程,在第 次循环 ,运行以下分步骤。
,运行以下分步骤。
1) 相关最大计算寻找最佳原子索引
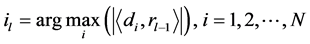
2) 更新原子索引集合

3) 更新子字典
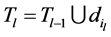
4) 更新系数估计
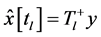
其中, 。
。
5) 更新残差
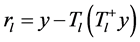
6) 判断终止条件,若 ,算法结束。
,算法结束。
步骤4:输出分解系数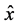 。
。
步骤5:合成稀疏信号
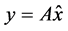
3. 稀疏度估计方法
3.1. 基于主成份分析的稀疏度估计方法 [1] [3]
对信号进行PCA变换后的系数特性进行分析,假设对于任意给定的自然场景图像,其PCA后的系数为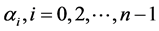 ,则该系数曲线可近似看作正态分布函数,其均值为
,则该系数曲线可近似看作正态分布函数,其均值为 ,方差
,方差 可通过下式得到。
可通过下式得到。

稀疏度K与方差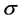 间存在如下的线性关系
间存在如下的线性关系
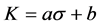
式中,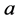 和
和 为常数,可以通过数据拟合的方式得到可以看出,当上述假设成立时,只需要对信号数据进行一次PCA得到变换后的系数,就可以通过上述两式对稀疏度进行估计。
为常数,可以通过数据拟合的方式得到可以看出,当上述假设成立时,只需要对信号数据进行一次PCA得到变换后的系数,就可以通过上述两式对稀疏度进行估计。
将得到的系数采用最小二乘方法进行拟合,拟合时直接采用Matlab7.x中的polyfit函数,该函数采用最小二乘法曲线拟合方法,所得到的函数值在基点处的值与原来点的坐标偏差最小。得到拟合公式为
 (2)
(2)
3.2. 基于噪声特性的稀疏度估计方法
在无噪声干扰的情况下,OMP算法会将信号 在字典 的作用下稀疏表示为指定稀疏度K的稀疏信号Y。当指定稀疏度K小于信号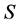 的真实稀疏度时,OMP算法会将信号S在频域中安频率分量的大小,从大到小选出K组频率分量输出为稀疏信号Y;当指定稀疏度K大于或等于信号S的真实稀疏度时,理论上有稀疏信号Y和信号
的真实稀疏度时,OMP算法会将信号S在频域中安频率分量的大小,从大到小选出K组频率分量输出为稀疏信号Y;当指定稀疏度K大于或等于信号S的真实稀疏度时,理论上有稀疏信号Y和信号 相等。在有噪声干扰的情况下,和无噪声干扰不同的是当指定稀疏度K大于或等于信号S的真实稀疏度时,稀疏信号Y和信号S不再相等,而是随着指定稀疏度K的增大,稀疏信号Y不仅会信号
相等。在有噪声干扰的情况下,和无噪声干扰不同的是当指定稀疏度K大于或等于信号S的真实稀疏度时,稀疏信号Y和信号S不再相等,而是随着指定稀疏度K的增大,稀疏信号Y不仅会信号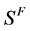 中的所有分量,而且还会有“杂波”。这些杂波本质上是噪声,在OMP算法中的过稀疏度表示时被误认为是信号有用频率分量。而且这些杂波的出现也有规律,即杂波出现的频率分量刚好是白噪声在该处能量最大的地方。噪声在整个频谱近似于均匀分布,即杂波出现的频点位置以均匀分布的方式依概率分布在全频域中。这个性质为我们估计稀疏度提供了理论支撑 [9] [10] 。
中的所有分量,而且还会有“杂波”。这些杂波本质上是噪声,在OMP算法中的过稀疏度表示时被误认为是信号有用频率分量。而且这些杂波的出现也有规律,即杂波出现的频率分量刚好是白噪声在该处能量最大的地方。噪声在整个频谱近似于均匀分布,即杂波出现的频点位置以均匀分布的方式依概率分布在全频域中。这个性质为我们估计稀疏度提供了理论支撑 [9] [10] 。
于是我们想到,可否现将信号 进行分段,然后每一段信号进行一次稀疏度为K的OMP分解,根据分解的结果,来判断稀疏度选择的正确性。若所有分段后的信号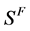 都相等,说明稀疏度选择过小,若不等,说明稀疏度选择过大,重复多次直到确定信号S的稀疏度。
都相等,说明稀疏度选择过小,若不等,说明稀疏度选择过大,重复多次直到确定信号S的稀疏度。
但单单依靠这个方法去估计稀疏度会存在一个问题,在逐步增大稀疏度K时,有可能在噪声较大时,估计的稀疏度偏小。这是因为OMP算法在对信号进行稀疏表示时,每次迭代只选取一个能量最大的频率分量造成的。当信号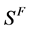 中有N个频率分量上的能量相差无几时,在噪声的干扰下,会随机的使其中一个频率分量的能量超过其他的频率分量,导致OMP算法在分解后出现不相同的
中有N个频率分量上的能量相差无几时,在噪声的干扰下,会随机的使其中一个频率分量的能量超过其他的频率分量,导致OMP算法在分解后出现不相同的 ,但这时指定稀疏度并未达到信号的真实稀疏度,而导致估计错误,我们称这类估计错误的原因为第二类误差。
,但这时指定稀疏度并未达到信号的真实稀疏度,而导致估计错误,我们称这类估计错误的原因为第二类误差。
针对这个问题,需要寻求一种新的稀疏度判别手段,对分段后的信号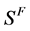 的频点位置进行统计,若新出现的频率分量的位置个数小于信号分段数的
的频点位置进行统计,若新出现的频率分量的位置个数小于信号分段数的 ,我们就有很大的把握相信出现了上面所说的第二类误差。若新出现的频率分量的位置数大于信号分段数的
,我们就有很大的把握相信出现了上面所说的第二类误差。若新出现的频率分量的位置数大于信号分段数的 ,这时我们有很大的把握相信预定的稀疏度选择过大。在分段数的选择上,一般选择大于信号
,这时我们有很大的把握相信预定的稀疏度选择过大。在分段数的选择上,一般选择大于信号 中最大 的三倍。
中最大 的三倍。
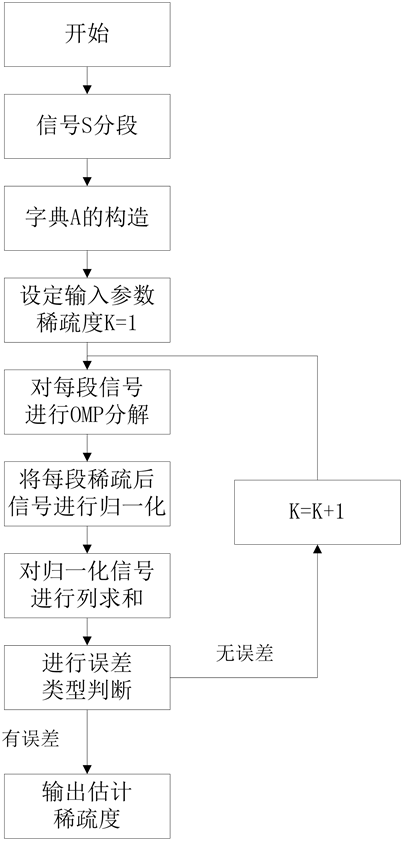
通过前面分析,信号稀疏度估计的步骤如下:
步骤1:将信号“S”进行分段为 。
。
步骤2:构造傅立叶基字典A。
步骤3:假定稀疏信号 的稀疏度K为1。对
的稀疏度K为1。对 依次进行OMP算法稀疏表示为
依次进行OMP算法稀疏表示为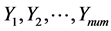 。即将
。即将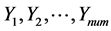 组成一个矩阵
组成一个矩阵 ,并将
,并将 中非零元素全部变为1,组成矩阵
中非零元素全部变为1,组成矩阵 ,然后对矩阵
,然后对矩阵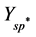 列求和得到
列求和得到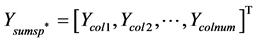 ,计算
,计算 满足条件
满足条件 的元素个数M,若存在大于等于分段数的个数M,则判断有误差,否则判断无误差。
的元素个数M,若存在大于等于分段数的个数M,则判断有误差,否则判断无误差。
步骤4:若存在误差,则执行步骤5,否则将稀疏度加1,再一次对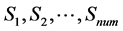 依次进行稀疏表示,执行步骤3。
依次进行稀疏表示,执行步骤3。
步骤5:将 作为估计后的稀疏度输出。
作为估计后的稀疏度输出。
实现框图如下:
4. 实验仿真验证
4.1. 基于主成份分析法的稀疏度估计方法验证
假设仿真信号由单频信号120 Hz起,步长为4 Hz,终止频率为132 Hz到154 Hz组成的6组正弦信号,运用上述(2)式进行稀疏度估计。估计结果如表1所示。
表1显示了在一维信号中,利用主成份分析方法对稀疏度进行估计的结果,结果显示该方法并不能有效的对一维信号进行有效的稀疏度估计。
4.2. 基于噪声特性分析法的稀疏度估计准确率随信噪比的变化
假设仿真信号由单频信号120 Hz起,步长为4 Hz,终止频率为160 Hz组成的正弦信号,幅值为5,6,1,6,4,1,2,4,6,6;经过高斯白噪声加扰形成。采样频率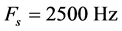 ,字典 起始频率为0 Hz,终止频率为250 Hz。误差门限设置为1倍信号分段数。信号长度为25,000,将该信号均分为10段,进行20次稀疏度估计。
,字典 起始频率为0 Hz,终止频率为250 Hz。误差门限设置为1倍信号分段数。信号长度为25,000,将该信号均分为10段,进行20次稀疏度估计。
运用本文的稀疏度估计方法对该仿真信号进行稀疏度估计准确率随信噪比变化如图1所示。

Table 1. System resulting data of sparsity estimation
表1. 稀疏度估计结果数据
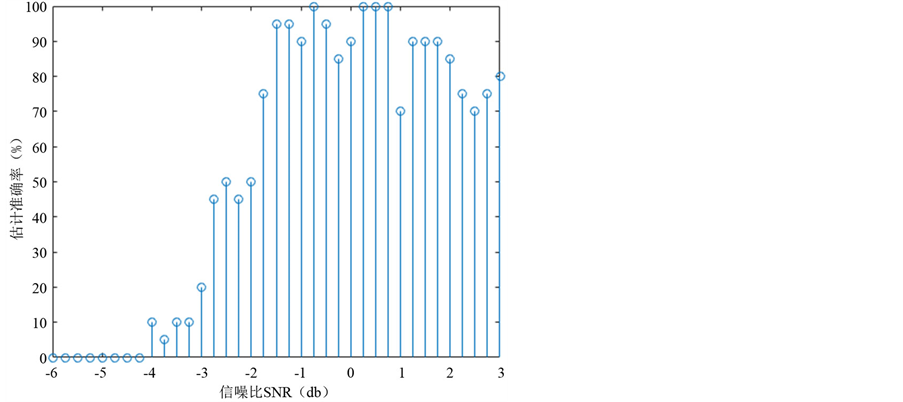
Figure 1. Stem: system result of sparsity estimation
图1. 标准试验系统结果线图
从图1可以看出,当信噪比小于−4 db时,信号稀疏度估计的准确率为零,此时信号受噪声干扰较为严重。当信噪比在−4 db至−1.5 db时,信号稀疏度估计的准确率随着信噪比的增大而增大。当信噪比在−1.5 db至0.75 db时,信号稀疏度估计的效果最好,可以达到85%以上。当信噪比大于0.75 db时,稀疏度估计的准确率不升反降,这是因为当信噪比过高时,起始频率与终止频率之差是250 Hz,在稀疏度为10的仿真信号中,误差稀疏度会以一定的概率重复出现在同一频点,导致估计稀疏度比真实稀疏度高1,导致稀疏度估计的准确率在90%左右。
5. 结论
本文利用含噪信号在全频域上的稀疏特性,构造了基于傅立叶基的完备原字库。再根据噪声特性,在冗余稀疏度条件下对含噪信号进行稀疏表示,运用本文的误差判别方法对信号稀疏度进行估计。实验表明,本方法可以在较低的信噪比噪声环境下对信号的稀疏度进行估计。相比之下,本文方法比利用主成分分析方法对信号稀疏度估计更为准确,在低信噪比的情况下依然可以对信号的稀疏度进行有效的估计。
基金项目
国家自然科学基金资助(61471378)。