1. 引言
目前发现了弱相互作用,且满足SU(2)群,强相互作用,且满足SU(3)群,电磁相互作用,且满足U(1)群。并且建立了标准模型(完成了强、弱电统一理论),SU(3) XSU(2) XU(1)。Georgi和Glashow 1974年提出大统一模型SU(5),但后来被质子衰变实验所排出。
2. 引力作用的群表示 [1]
设引力场为
 (2.1)
(2.1)
其拉氏量密度:
 (2.2)
(2.2)
显然上式在U(4)整体规范变换
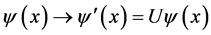 (2.3)
(2.3)
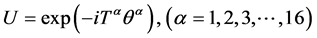 (2.4)
(2.4)
下不变的。其中 是与x无关的16个实参数,
是与x无关的16个实参数, 是U(4)群的16个生成元。
是U(4)群的16个生成元。
它们满足群代数
 (2.5)
(2.5)
以及正交关系:
 (2.6)
(2.6)
为了讨论定域规范不变性,将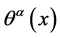 代替
代替 得:
得:
 (2.7)
(2.7)
此时,场的导数为:
 (2.8)
(2.8)
由于右边多出第一项,所以,拉氏密度在(2.3) (2.7)变换下不是不变量。要想不变,则要找出协变导数。
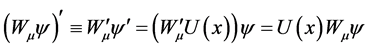 (2.9)
(2.9)
比较上式的系数得:
 (2.10)
(2.10)
为了简化,引进矩阵矢量引力规范场:
 (2.11)
(2.11)
协变微商为:
 (2.12)
(2.12)
所以
 (2.13)
(2.13)
所以:
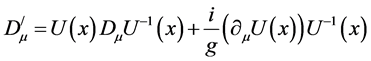 (2.14)
(2.14)
规范场 是按
是按 标架传播的,这样的规范场矢量
标架传播的,这样的规范场矢量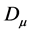 传递的是动量。
传递的是动量。
所以有:
 (2.15)
(2.15)
如果把规范场看成动力学场,则必须引进规范场的拉氏量密度,并要求它在变换(2.14) (2.3)、(2.7)下不变。为此,引进引力规范场张量:定义
 (2.16)
(2.16)
或定义:
 (2.17)
(2.17)
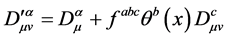 (2.18)
(2.18)
可以看出: 是变换(2.14) (2.7)、(2.3)下的不变量。可以取它为引力规范场的拉氏量密度即:
是变换(2.14) (2.7)、(2.3)下的不变量。可以取它为引力规范场的拉氏量密度即:
 (2.19)
(2.19)
这样就得到了在引力定域规范变换式(2.14) (2.7)、(2.3)下不变的拉氏量密度:
 (2.20)
(2.20)
上式右边第三项是U(4)域规范不变性确定的物质场与引力规范场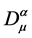 之间的相互作用,是同位旋流,耦合常数g表征了相互作用强度。此外,与阿贝尔情形不同的是,在非阿贝尔情况下,由于
之间的相互作用,是同位旋流,耦合常数g表征了相互作用强度。此外,与阿贝尔情形不同的是,在非阿贝尔情况下,由于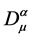 中除了导数外,还有
中除了导数外,还有 的乘积项,故上式右边第二项含有
的乘积项,故上式右边第二项含有 的3次和4次项,它们表示了引力规范场的自相互作用。
的3次和4次项,它们表示了引力规范场的自相互作用。
综上所述,如果是4个态的引力场,在U(4)定域规范变换(7.3.4.3) (7.3.4.7)下不变,则必须引进16个规范场,它们按定域规范变换式(7.3.4.14)变换,并与4重态的同位旋矢量流耦合确定它们之间的相互作用。由于U(4)群的非阿贝尔性,引力规范场张量中除了散度项外,还有引力规范场的乘积项,这规定了引力规范场还有自相互作用。
3. G真空模型
3.1. G真空定理
本人首次给出如下真空定义及定理:
真空定义:静质量为零的物质态。
真空定理1:在真空内,物质是以波的形式存在的。
真空定理2:真空内的物质满足线性关系。
真空定理3:真空内的物质态是可以叠加的。
真空定理4:真空物质态是非色散的(色散度为零)。
真空定理5:真空内一切物质态都是以真空光速运动的。
3.2. 真空自发对称性破缺 [2]
在复时空标量场内的拉格朗日量的密度为:
 (3.2.1)
(3.2.1)
其相互作用势为:
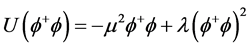 (3.2.2)
(3.2.2)
当 、
、 都为大于零的实数时,相互作用势的最小值并不发生在
都为大于零的实数时,相互作用势的最小值并不发生在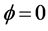 处,因此
处,因此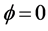 并不是复时空标量场系统的真空态,如图1。为了找出系统的真空点,只需求出
并不是复时空标量场系统的真空态,如图1。为了找出系统的真空点,只需求出 的最小值。容易求得最小值点为:
的最小值。容易求得最小值点为:
 (3.2.3)
(3.2.3)
不失一般性,可以取任意角,令 。因为系统具有U(1)旋转不变性,
。因为系统具有U(1)旋转不变性,
即使取
 (3.2.4)
(3.2.4)
任意相角 也可通过U(1)变换
也可通过U(1)变换 再次产生出来。相角
再次产生出来。相角 是时空角,是不可观测量。当真空点相角确定之后,系统U(1)旋转对称性就消失了,这种系统所具有的对称性因物理真空点的移动而消失的现象称为真空自发对称性破缺(真空相变)。
是时空角,是不可观测量。当真空点相角确定之后,系统U(1)旋转对称性就消失了,这种系统所具有的对称性因物理真空点的移动而消失的现象称为真空自发对称性破缺(真空相变)。
考虑到真空点的移动,我们重新定义复时空标量场为:
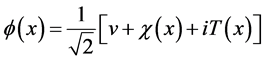 (3.2.5)
(3.2.5)
将上式带入复时空标量场作用势得:
 (3.2.6)
(3.2.6)
上式最后一步用了
 (3.2.7)
(3.2.7)
去掉(3.2.6)中对相互作用没有贡献的常数项,则复时空标量场的拉格朗日量密度可用实标量场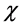 和T表示出来。
和T表示出来。
即:
 (3.2.8)
(3.2.8)
上式说明场空间 获得了静止质量,而时间T依然无静止质量。
获得了静止质量,而时间T依然无静止质量。
即:
 ,而
,而 (3.2.9)
(3.2.9)
对称性破缺后,空间标量场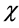 和时间标量场T的质量为:
和时间标量场T的质量为:
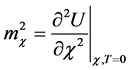 ,
,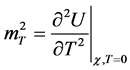 (3.2.10)
(3.2.10)
可以利用(3.6)验证上式与(3.2.9)式相符。通过(3.2.5)式可知:
 (3.2.11)
(3.2.11)
 (3.2.12)
(3.2.12)
从图1,可以看出,在破缺后的真空点处,相互作用势沿空间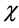 增加方向的二次导数不为零,从物理效果上看,这相当于X获得了质量。而沿时间T增加的方向上,即在势函数的低谷方向,旋转对称性依然存在,在此方向上相互作用势的二次导数为零,时间标量场T仍无静质量。这里我们看到,对称性破缺会使空间场获得静质量,同时会在正切于对称性破缺的方向(时间方向)产生静质量为零的粒子,这是自发对称性破缺机制的一个必然结果。这样产生的静质量为零的粒子称为古德斯通(GoldStone)粒子。
增加方向的二次导数不为零,从物理效果上看,这相当于X获得了质量。而沿时间T增加的方向上,即在势函数的低谷方向,旋转对称性依然存在,在此方向上相互作用势的二次导数为零,时间标量场T仍无静质量。这里我们看到,对称性破缺会使空间场获得静质量,同时会在正切于对称性破缺的方向(时间方向)产生静质量为零的粒子,这是自发对称性破缺机制的一个必然结果。这样产生的静质量为零的粒子称为古德斯通(GoldStone)粒子。
4. G超统一模型
4.1. G超统一模型的直积群表示
G超统一模型可用直积群表示即:U(1) XSU(2) XSU(3) XU(4)。
该群元为:
 (4.1.1)
(4.1.1)
该直积群协变微商为 [3] :
 (4.1.2)
(4.1.2)
( 电磁规范场;
电磁规范场;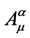 弱作用规范场;
弱作用规范场; 强作用规范场;
强作用规范场; 引力规范场;
引力规范场;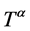 电磁群生成元,
电磁群生成元, 弱作用生成元,
弱作用生成元, 强作用生成元,
强作用生成元, 引力生成元。其中
引力生成元。其中 ;
; ;
; ;
; 。)
。)
4.2. G超统一模型的单群表示
可用二十维幺正单群U(20)表示G超统一模型。
设引力场为
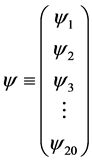 (4.2.1)
(4.2.1)
 (4.2.2)
(4.2.2)
显然上式在U(20)整体规范变换
 (4.2.3)
(4.2.3)
 (4.2.4)
(4.2.4)
下不变的。其中 是与x无关的400个实参数,
是与x无关的400个实参数, 是U(20)的400个生成元。它们满足群代数
是U(20)的400个生成元。它们满足群代数
 (4.2.5)
(4.2.5)
以及正交关系:
 (4.2.6)
(4.2.6)
为了讨论定域规范不变性,将 代替
代替 得:
得:
 (4.2.7)
(4.2.7)
此时,场的导数为:
 (4.2.8)
(4.2.8)
由于右边多出第一项,所以,拉氏密度在(4.2.3) (4.2.7)变换下不是不变量。要想不变,则要找出协变导数。
 (4.2.9)
(4.2.9)
比较上式的系数得:
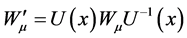 (4.2.10)
(4.2.10)
为了简化,引进矩阵矢量超统一规范场:
 (4.2.11)
(4.2.11)
协变微商为:
 (4.2.12)
(4.2.12)
所以
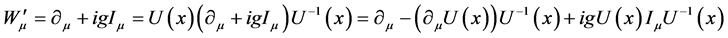 (4.2.13)
(4.2.13)
所以:
 (4.2.14)
(4.2.14)
超统一规范场 是按
是按 标架传播的,这样的规范场矢量
标架传播的,这样的规范场矢量 传递的是动量。
传递的是动量。
所以:
 (4.2.15)
(4.2.15)
如果把规范场看成动力学场,则必须引进规范场的拉氏量密度,并要求它在变换(4.2.3) (4.2.7) (4.2.14)下不变。为此,引进超统一规范场张量:定义
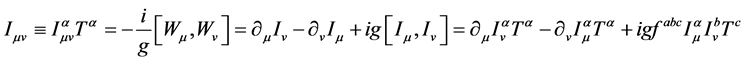 (4.2.16)
(4.2.16)
或定义:
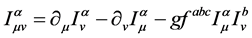 (4.2.17)
(4.2.17)
 (4.2.18)
(4.2.18)
可以看出: 是变换(4.2.3) (4.2.7) (4.2.14)下的不变量。可以取它为超统一规范场的拉氏量密度即:
是变换(4.2.3) (4.2.7) (4.2.14)下的不变量。可以取它为超统一规范场的拉氏量密度即:
 (4.2.19)
(4.2.19)
这样就得到了在超统一定域规范变换式(4.2.3) (4.2.7) (4.2.14)下不变的拉氏量密度:
 (4.2.20)
(4.2.20)
上式右边第三项是U(20)域规范不变性确定的物质场与超统一规范场 之间的相互作用,是同位旋流,耦合常数g表征了相互作用强度。此外,与阿贝尔情形不同的是,在非阿贝尔情况下,由于
之间的相互作用,是同位旋流,耦合常数g表征了相互作用强度。此外,与阿贝尔情形不同的是,在非阿贝尔情况下,由于 中除了导数外,还有
中除了导数外,还有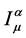 的乘积项,故上式右边第二项含有
的乘积项,故上式右边第二项含有 的3次和4次项,它们表示了超统一规范场的自相互作用。
的3次和4次项,它们表示了超统一规范场的自相互作用。
所以,如果是20个态的超统一场,在U(20)定域规范变换(4.2.3) (4.2.7)下不变,则必须引进400个规范场,它们按定域规范变换式(4.2.14)变换,并与20重态的同位旋矢量流耦合确定它们之间的相互作用。由于U(20)群的非阿贝尔性,超统一规范场张量中除了散度项外,还有超统一规范场的乘积项,这规定了超统一规范场还有自相互作用。
如图2所示,随着宇宙膨胀,温度不断降低,并不断发生相变,即:当宇宙大爆炸后 秒时,第一次对称性破缺(宇宙发生相变,引力分离出来,即时空创生了)。
秒时,第一次对称性破缺(宇宙发生相变,引力分离出来,即时空创生了)。
 (4.2.21)
(4.2.21)
当宇宙大爆炸后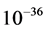 秒(能量为
秒(能量为 )时,第二次对称性破缺(相变),强作用分离出来,即:
)时,第二次对称性破缺(相变),强作用分离出来,即:
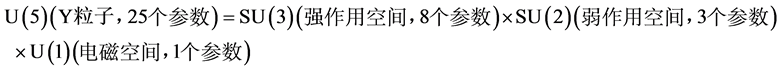 (4.2.22)
(4.2.22)
当宇宙大爆炸后 秒时,第三次对称性破缺(相变),弱作用分离出来,留下一维电磁相互作用保持U(1)性质(因为强、弱相互作用是短程力,所以有幺模限制,电磁力、引力势长程力所以没有幺模限制)。
秒时,第三次对称性破缺(相变),弱作用分离出来,留下一维电磁相互作用保持U(1)性质(因为强、弱相互作用是短程力,所以有幺模限制,电磁力、引力势长程力所以没有幺模限制)。
另外,引力空间破缺后,形成轻子空间和夸克空间,两空间相互作用形成了我们现在生活的三维全对称实空间和一维反对称虚空间---时间,当时空的弯曲等同于力的作用。
即:
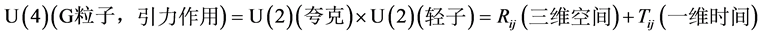 (4.2.23)
(4.2.23)
5. G超统一矢量表示
5.1. G荷
设五维矢量F,则有:
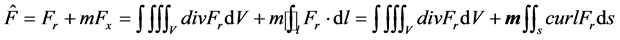 (5.1.1)
(5.1.1)
(m为第五维矢量。)
令四维矢量
 (5.1.2)
(5.1.2)
g荷定义:即:在时间、空间、能量空间、色空间内的统一荷为G荷。
数学表述:
 (5.1.3)
(5.1.3)
即:四维G矢量的散度对三维闭合面所包围的四维体积的积分。
G荷在空间里的投影形成电荷q,在时间维投影里形成弱荷t,在色空间投影形成色荷s,在能量空间里投影形成质荷m。
可用四元数表示: 即由相互垂直的时间t、空间r、色空间s、能量维e的直和构成的。
 (5.1.4)
(5.1.4)
(其中 。)
。)
我们取时间和空间为水平两个互为垂直的轴,能量维和色维的绝对值为纵坐标的上半轴和下半轴,绘成G超时空四元数模型示意图(如图3)。四维矢量G与能量维的夹角 ,其
,其 形成能量荷(质量);G矢量与色维的夹角为
形成能量荷(质量);G矢量与色维的夹角为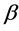 角,其
角,其 形成了色荷;G矢量与空间夹角为
形成了色荷;G矢量与空间夹角为 ,其
,其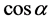 形成电荷;G矢量与时间维的夹角为
形成电荷;G矢量与时间维的夹角为 ,其
,其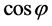 形成弱荷。
形成弱荷。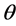 为时空角。时空角
为时空角。时空角 定义:四维矢量G在时空中投影矢量与空间维的夹角。
定义:四维矢量G在时空中投影矢量与空间维的夹角。
并有:
 (5.1.5)
(5.1.5)
即
 (5.1.6)
(5.1.6)
且有:
 (5.1.7)
(5.1.7)
我们在G坐标系内做G超时空四元数的示意图。当 (即能量角一定,弱角(时空角)一定时,则粒子运动速度恒定,即
(即能量角一定,弱角(时空角)一定时,则粒子运动速度恒定,即 ,此时粒子无论做怎样的惯性运动,此时系统动量均守恒;当
,此时粒子无论做怎样的惯性运动,此时系统动量均守恒;当 (能量角一定,时空角变化)时,即
(能量角一定,时空角变化)时,即 则该粒子做非费惯运动(即粒子在空间长时间运动或相互作用,此时,粒子的物理性质将发生变化,动量不再守恒,但系统总能量是守恒的。
则该粒子做非费惯运动(即粒子在空间长时间运动或相互作用,此时,粒子的物理性质将发生变化,动量不再守恒,但系统总能量是守恒的。
可以说,动量守恒是有条件的,即极短时间内的作用下,动量是近似守恒的。但只要能量角一定,无论在整个时空内怎样的运动(或作用),系统的总能量是守恒的。看得出,能量守恒比动量守恒更普遍,

Figure 3. Super G complex spatiotemporal model
图3. G超复时空模型
但在超出时空维度的高维空间里的作用,其能量不一定是守恒。上面就是旋转对称性与物理量守恒的对应关系。
能量维在空间的投影形成了粒子的三代;时间维在空间的投影形成了粒子过去、现在、将来,这导致了粒子在空间运动,即粒子的不确定性;色维在空间的投影形成了红蓝绿三种色荷。
G积分定理:
设四维空间有界闭合区域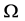 ,其边界
,其边界 为分片光滑三维闭曲面。函数
为分片光滑三维闭曲面。函数 及其一阶偏导数在
及其一阶偏导数在 上连续,那么有:
上连续,那么有:
 (5.1.8)
(5.1.8)
(E能量,e能量坐标,T时间量,t时间坐标,R空间量,r空间坐标,S色空间量,s坐标,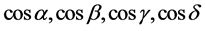 分别为能量、时间、空间、色空间维的外法方向余弦,
分别为能量、时间、空间、色空间维的外法方向余弦, 为四维体积。)
为四维体积。)
即:
 (5.1.9)
(5.1.9)
即:G矢量穿过任意封闭三维曲面(超曲面)的通量等于G矢量的散度对三维闭合面所包围的体积的积分,等于封闭超曲面(三维曲面)所包围的g荷量代数和。
5.2. H荷
因:
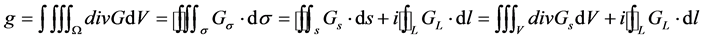 (5.2.1)
(5.2.1)
(上式右边第一项反应了散度特性,第二项反应了旋度特性。)
定义h荷:
即h荷等于G矢量在能量维、空间维、色维中的总投影矢量的散度在上述三空间的积分值。即,g荷在能量维、空间维、色维空间内的统一荷为h荷。
数学表述:
 (5.2.2)
(5.2.2)
同理:定义u荷:
 (5.2.3)
(5.2.3)
即G矢量在能量维和空间维内的总投影矢量的散度在能量维和空间维的积分值。
定义质量:
 (5.2.4)
(5.2.4)
即G矢量在能量维的投影的散度在能量维的积分。
定义电荷:
 (5.2.5)
(5.2.5)
( )
)
即G矢量在空间维的投影的散度在空间维的积分。
定义强荷(色荷):
 (5.2.6)
(5.2.6)
即G矢量在色空间的投影的散度在色空间的积分。
定义弱荷(时间):
 (5.2.7)
(5.2.7)
即G矢量在时间内的投影的散度在时间内的积分。
6. 结束语
G超统一论,提出了G超统一群及GY粒子,详细阐述了引力的相互作用。首次提出G宇宙标准模型U(1) XSU(2) XSU(3) XU(4),并用U(20)超群统一描述了宇宙随温度的不断降低而导致的不断破缺的演化过程。揭示了时间和空间的起源、四种相互作用的成因。