1. 引言
同步是指多个系统在某种耦合作用下各个系统的状态趋向一致，它是物理、生物、化学等系统中的一种普遍现象，已引起广泛兴趣和研究 [1] - [4] 。最早的研究主要是针对某一特定结构的耦合系统的同步性，其中Carroll和Pecora研究了混沌系统线性耦合的同步问题并提出了主稳定性函数(Master Stability Function，简记为MSF)的方法 [1] ，这方法被推广到研究任意结构的动力学网络系统，并用于神经网络、通信、控制等许多领域的网络系统同步问题 [2] - [6] 。
Hindmarsh-Rose(简记为HR)动力学系统是生物学上一个著名的单神经元模型 [7] ，该模型很好地解释了神经元的脉冲放电、簇放电和混沌行为等动力学特性。近年来，HR神经元模型被广泛应用于神经非线性动力学稳定性问题，如脉冲放电和簇放电间的转换问题 [8] 、HR模型的随机分叉问题 [9] 、两个HR神经元的耦合问题 [5] 和特定网络结构的耦合问题 [6] ，以及通过神经元网络同步问题来揭秘大脑工作机制等 [2] 。然而，HR神经元网络作为大脑的各种功能的模型，怎样调控神经元网络的同步和稳定性非常重要，仍有很多问题未解决，比如，基于HR模型的神经网络的结构与参数空间动力学同步稳定性分析仍未完全清楚。
本文我们先研究HR模型的动力学，给出引起神经元放电的临界激励行为，然后，考虑由HR神经元线性耦合组成的网络动力学，及其同步稳定性，我们应用主函数(MSF)方法分析HR神经元网络动力学系统的同步稳定性，分析系统参数对同步稳定性的影响。文章的第1部分是引言；第2部分主要介绍了HR神经元模型，并给出动力学分析，及其神经元放电的临界行为；第3部分，我们主要介绍网络同步稳定性分析的主函数方法；第4部分，我们给出HR神经元网络动力学系统参数空间的同步稳定性相图；最后我们给出讨论和结论。
2. Hindmarsh-Rose神经元模型
上世纪50年代，Hodgkin和Huxley首先提出了用微分方程来描述神经元放电的Hodgkin-Huxley(简记为HH)模型 [10] ，该模型成功的说明了神经元的脉冲放电(spiking，即连续脉冲)和动作电位的产生机理，但不能够描述神经元的簇放电(bursting，即连续脉冲和静息状态交替出现)行为。1984年，Hindmarsh和Rose在HH模型的基础上加入一慢电流项，这样可以很好地的解释神经元的脉冲和簇放电行为。HR模型可以写为 [7] ：
(1)
其中x是神经元的膜电位，y为Na和K离子通过膜上快离子通道的速率，z为其他离子通过膜上慢离子通道的速率，I表示外界直流激励电流，x0为阈值电位(文章中取为−1.6)，μ为描述膜上慢离子通道速率的参数。
我们先应用数值方法解方程(1)并给出HR神经元模型各变量随时间变化的规律(见图1)。其中，时间精度为0.01 s，μ = 0.001，I = 2.5，截取2000 s~3000 s是为了变量稳定。我们可以看到神经元的膜电位和Na和K离子通道的速率同步脉动，而其他离子通道的速率随时间小幅度的脉动。
我们考虑不同的膜上慢离子通道速率的参数 和外界直流激励电流 对膜电位动力学行为的影响。我们先给定 = 0.001，激励电流I分别取为1.5，2.5和3.5，给出对应的膜电位x随时间t的变化曲线(见图2)。图2中(a)和(b)可以看出：当激励电流I = 1.5，2.5时，膜电位出现簇放电现象；但当激励电流I = 3.5(见(c))时，簇放电现象消失。对于不同μ值，也可以得到类似的结果。这说明了当受到强烈外界刺激时，神经元将会表现出持续的脉冲放电反应；当受到弱外界刺激时，神经元将会表现出持续的簇放电反应。这与采用电压钳方法的蜗牛神经实验的结论一致 [7] ，这也证明了我们的数值解是正确的。
为了给出激励对簇放电的影响，我们定义簇放电中静息状态的时长为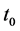
，连续脉冲的平均时长为
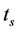，用比值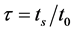
来定量描述HR神经元的放电行为。当
时，表示HR神经元处于脉冲放电状态；当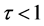
时，表示HR神经元处于簇放电状态。我们设 = 0.001，激励电流I取为3~3.4，给出对应的τ随电流I的变化曲线(见图3)。从图3可以看出在激励电流I从3.26到3.27时，τ值突然从0.1变为1，说明HR神经元放电行为发生了突变，由簇放电变为脉冲放电。对于不同的μ值，也可以得到类似的结果。这说明了神经元放电行为存在一个临界值，当外界刺激超过该临界值时，则神经元将会表现出放电状态的突然转变。
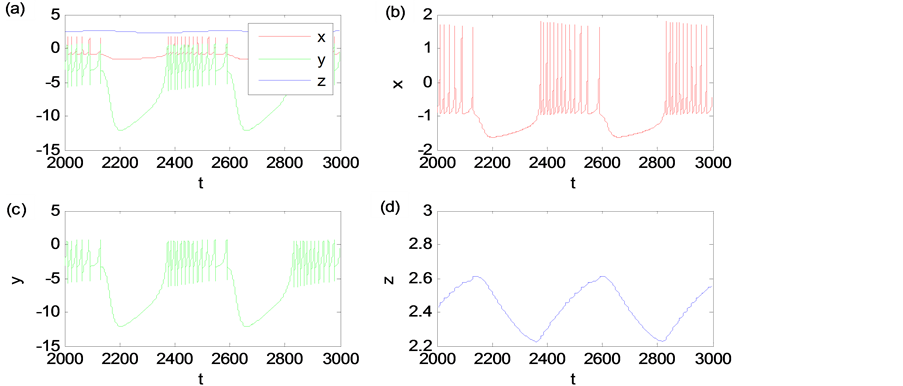
Figure 1. (a) The time evolution of the HR neuronal model (x, y, z); (b) The action potential x; (c) The fast ionic fluxes y; (d) The slow ionic fluxes z
图1. (a) HR神经元模型的时间演化曲线(x, y, z)；(b) 膜电位x; (c) 快变量(Na和K离子速率)y; (d) 慢变量(其他离子速率)z
Figure 2. The time evolution of the action potential x. (a) The bursting for I = 1.5; (b) I = 2.5; (c) The spiking for I = 3.5; μ = 0.001
图2. 膜电位的时间演化曲线x。(a) 簇放电，其中 I = 1.5；(b) I = 2.5；(c) 脉冲放电，其中I = 3.5；μ = 0.001
Figure 3. The mutation of τ = ts/t0, form 0.1 to 1,for μ = 0.001
图3. 放电模式突变，τ = ts/t0由0.1突变为1，其中μ = 0.001
对于给定模型激励电流I = 2.5，膜上慢离子通道速率的参数 分别为0.001、0.0055和0.01，并给出对应的膜电位x随时间t的变化曲线(见图4)。我们发现图4中(a)、(b)和(c)三种情况都出现了神经元膜电
Figure 4. Time evolution of the action potential (a) (b) and (c), bursting for μ = 0.001, 0.0055, 0.01. The number of peaks is different in a discharge cycle
图4. 神经元的膜电位(a) μ = 0.001；(b) μ = 0.0055；(c) μ = 0.01三种情况都出现簇放电现象，但是每一个放电周期中出现连续脉冲的数目不同
位的簇放电现象，但是每一个放电周期中出现连续脉冲的数目不同，μ越大，脉冲数目越小，对于I的其他值(不包括强烈刺激)，也出现类似的规律，图3和图4结果是之前没有人给出过的。
可见，当神经元受到的外界刺激比较弱时，神经元膜电位会出现持续的簇放电反应；当外界刺激超过某特定临界值时，神经元膜电位会突变为持续的脉冲放电反应，簇放电现象消失；而控制参数μ可以用来控制簇放电中连续脉冲的数目，从而可以调控模型适用于不同神经元细胞。
3. 网络同步稳定性分析的主稳定性函数方法
对于线性耦合的网络模型，Pecora和Carroll提出了用主稳定性函数方法来研究网络同步稳定性 [1] 。我们应用这方法分析HR神经元网络的同步稳定性。考虑网络的每个节点i有一个相同的HR神经元动力学系统F(Xi)，相互连接的节点之间存在耦合强度为σ的线性耦合HXj，因此网络的动力学方程可以表示为 [1] ：
(2)
其中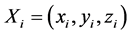
为矢量表示HR神经元的变量，F(Xi)表示HR神经元模型，即方程(1)的右边，
为网络的拉普拉斯矩阵(Laplacian)，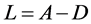
,其中
是对角矩阵，ki是网络节点的度数，A是网络的连接矩阵。H为一个3 × 3的矩阵，表示节点的耦合方式。当网络达到同步时，
。在同步状态解s附近对(2)式右边做幂级数展开，并取线性近似，设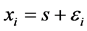
，方程(2)变为
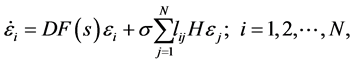(3)
其中εi为节点i在同步解s上的偏差；DF表示F的雅可比矩阵(Jacobian)。根据约丹规范型(Jordan canonical forms)理论，对角化方程(3)中的L矩阵给出特征值γi，其对应的特征向量为ei，并令η = eε，将e(本征矢组成的矩阵)右乘(3)式，方程(3)简化为 [1]
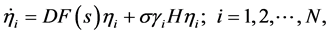(4)
其中γi为矩阵L的特征值。不失一般性，令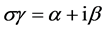
，对于无向图，矩阵L是对称的，其特征值γi为实的，对于有向图，矩阵L有可能是非对称的，对于非对称的L，其特征值γi为复的。对于给定的网络，α和β是给定的，这样就得到主稳定性方程 [1] ：
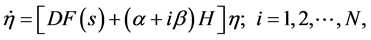(5)
根据李雅普诺夫稳定性理论，可以解出上式右边矩阵的特征值λi，当Re(λmax) < 0，网络同步稳定，否则网络同步不稳定，这就是主稳定性函数的方法。对于任意的网络结构都可以通过计算最大李雅普诺夫指数(Lyapunov exponents，记为λmax)随α和β的变化关系，从而分析网络的同步稳定性。这方法可以用于一般的线性耦合的网络系统。
4. HR神经元网络同步的稳定性分析
我们应用上述MSF方法分析HR神经元网络模型的动力学系统，即将方程(1)作为F代入方程(5)，其中令μ = 0.01，I分别取2.5和3.5来表示簇放电和脉冲放电这两种情况。对于HR神经元网络模型，由于在生物功能和网络同步方面主要是膜电位的耦合 [6] ，这里我们也只考虑膜电位x之间的线性耦合，即
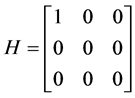(6)
我们考察网络同步解的稳定性，神经元系统(1)存在三个平衡态解，其中一个为实数解(x，y，z为实数)，另外两个是一对共轭复数解(x，y，z为复数)。事实上，神经元平衡态的复数解的物理和生物学意义并不清楚，有待进一步研究 [9] 。我们只讨论实数解。
对于平衡态的实数解，我们给出李雅普诺夫指数λmax在网络结构参数空间中的相图，见图5(a) 、图5(b)，其中μ = 0.01，I = 2.5，可以看出图5(b)中的λmax < 0区域给出对应的神经网络平衡态是同步稳定的，λmax > 0的区域是同步不稳定的。
由于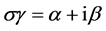
，因此，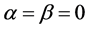
等价于网络没有耦合，这时HR神经元模型本身就是混沌的，从图5(b)也可以看出李雅普诺夫指数大于0。对于β = 0，当α(<0)增加，λmax是由正变为负的。这就说明,强的耦合(较大的σγ值)会使同步状态稳定。
我们知道外界激励电流I可以调控神经元放电行为，因此,我们分析了I对网络同步稳定性的影响。我们选定μ = 0.001，I为3~3.4(临界值大约为3.265)，网络为n维超立方体图(Hypercube Graph)结构(γmax = −2)，对HR神经元网络模型进行了分析，结果见图6(a)、图6(b)。从图6(b)可以看出来在临界值周围，I对模型同步稳定性影响不大，这说明神经元的放电模式对于神经元网络的同步稳定性并不是决定因素，主要影响因素是耦合强度(σ)和网络结构(γmax)。
为了给出模型参数和激励对网络同步稳定性的影响，在给定网络的结构和节点间的耦合强度(α = −0.5，β = 0)的情况下，对于平衡态解，我们给出李普诺夫指数在(μ,I)空间中的相图，见图7(a)、图7(b)，类似地，李普诺夫指数为负的区域，网络为同步稳定，正的区域为不稳定。从图7(b)可以看出：当网络结构和耦合强度(α = −0.5)一定时，对于外界激励电流I，强的外界激励电流可以使得同步达到稳定，这是
Figure 5. Master stability function for x-coupled HR neurons. (a) 3D map; (b) Contour map
图5. x耦合HR神经元主稳定性函数。(a) 三维图；(b) 等高图
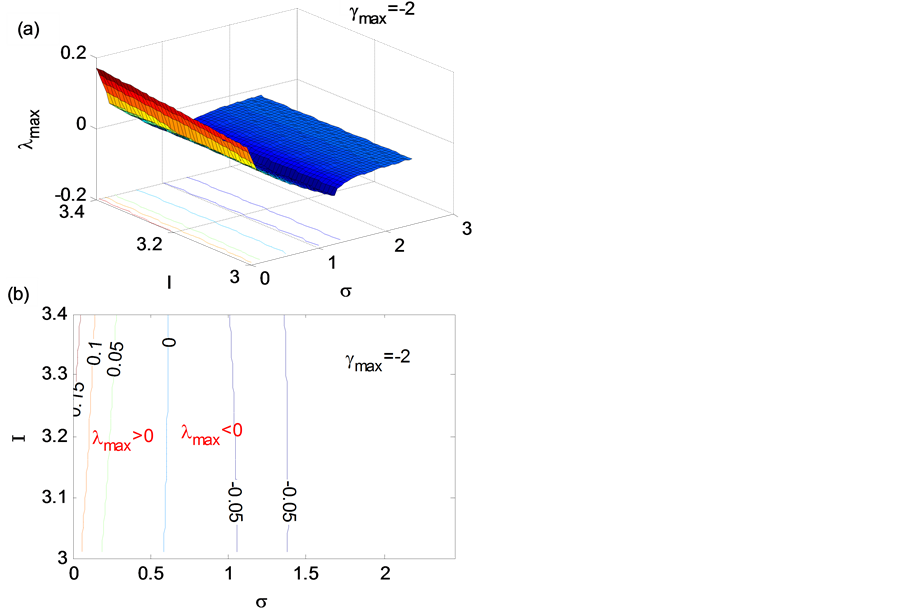
Figure 6. The influences of neural firing pattern on synchronous stability. (a) 3D map; (b) Contour map
图6. 放电形式对稳定性的影响。(a) 三维图；(b) 等高图
可以理解的，因为外界激励过于强大，自然各节点会趋于同步稳定；在较弱的外界激励电流的情况下，也是可以使得网络达到同步稳定的。而且当外界激励电流I使网络同步不稳定时，μ增大对网络同步稳定有好处。
4. 总结
我们介绍了HR模型，分析了神经元的脉冲放电和簇放电行为，给出了不同模型参数对模拟神经元放电行为的影响。我们发现：当神经元受到的外界刺激比较弱时，神经元膜电位会出现持续的簇放电反应；当外界刺激超过某特定临界值时，神经元膜电位会突变为持续的脉冲放电现象，簇放电现象消失，
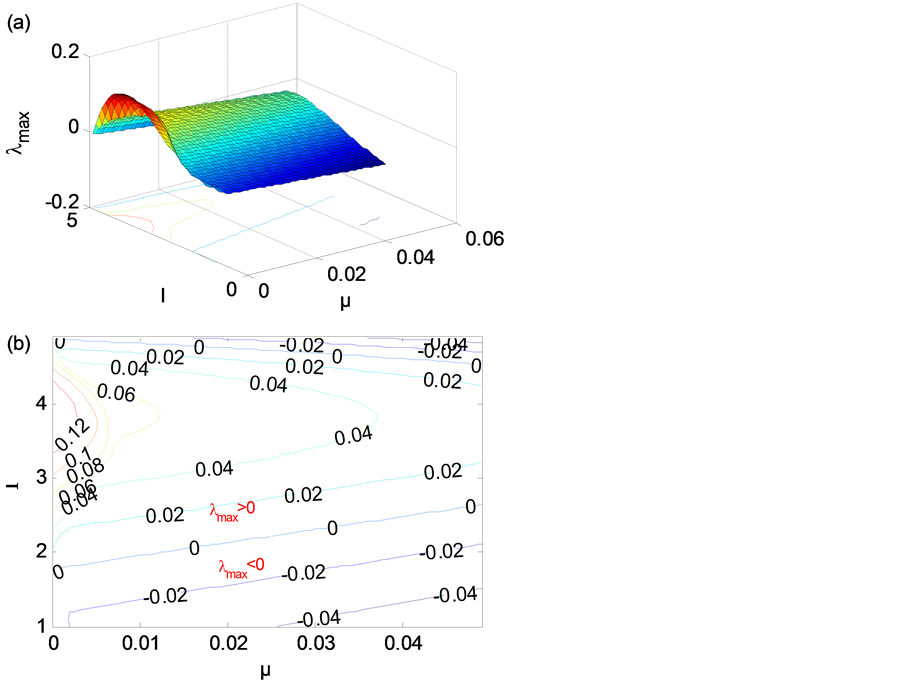
Figure 7. MSF of HR neurons in the (μ,I) space. (a) 3D map; (b) Contour map
图7. 李普诺夫指数在(μ,I)空间中的相图。(a)三维图；(b)等高图
因此我们引进了脉冲时间比τ来描述神经元的膜电位由簇放电突变为持续的脉冲放电的临界行为；同时我们发现控制参数μ可以用来控制簇放电中连续脉冲的数目，从而可以调控模型适用于不同神经元细胞。
另外，我们研究了由HR神经元通过线性耦合组成的网络动力学系统，我们利用主稳定性函数的方法分析HR神经元网络的同步稳定性，我们发现：在临界值周围，外界激励电流I对模型同步稳定性影响不大，神经元的放电模式对于神经元网络的同步稳定性并不是决定因素，主要影响因素是耦合强度(σ)和网络结构(γmax)。我们分析了模型控制参数μ和外界激励电流I对HR神经元网络的同步稳定性的影响，并发现：当网络结构和耦合强度(α = −0.5)一定时，对于外界激励电流I，不仅强的外界激励电流可以使得同步达到稳定，而且在较弱的外界激励电流下，也可以使得网络达到同步稳定的；并且当外界激励电流I使网络同步不稳定时，增大μ对网络同步稳定有好处。
基金项目
感谢光电材料与技术国家重点实验室和广东省显示材料与技术重点实验室的资助。