1. 引言
双目立体视觉技术目前广泛应用于视频监视,人机交互,军事领域,医学等方面,随着科技的发展,双目立体视觉技术将会占有举足轻重的地位。双目立体视觉技术主要集中在相机标定和立体匹配部分,其中立体匹配是立体视觉最为关键的部分。基于其立体匹配的应用要求,一种同时具备准确性和高效性的图像匹配技术成为重要需求。在目前的立体匹配算法中,由于SIFT算法在特征点尺度,旋转和光照不变性方面明显优于其他特征描述子,因此得到广泛应用。但SIFT描述子的维度较高从而计算过于复杂,为了降低计算复杂度,提高匹配精度,有很多研究人员提出了各种基于SIFT的改进算法。Bay等人提出的快速鲁棒特征(Speeded Up Robust Features, SURF)算法 [1] 类似于SIFT算法,特征点检测都是基于尺度空间,该算法采用Harr小波变换增加鲁棒性和Hessian矩阵来提高时间效率,同时以大大减少的特征点数目为代价;GLOH的方法 [2] 采用环形扇区代替矩形区域构建梯度位置直方图描述算子,再使用PCA将272维描述符降为128维,该描述算子的独特性比SIFT要好,但是计算更复杂;Kc和Sukthankar [3] 将主成分分析(PCA)方法运用至SIFT图像匹配中,采用主成分分析的方法对SIFT算子进行降维操作,其算法中特征点描述算子的维度可以降低到20维但是在执行快速匹配时的精度也不如SIFT [4] 。
本文考虑到PCA-SIFT算法在速度上的优势和精度不高的缺点,结合由Fischler和Bones于1981年提出的RANSAC算法思想 [5] ,综合利用二者的优势,提出了一种PCA-SIFT算法和RANSAC算法相结合的立体匹配方法。首先,采用PCA-SIFT算法提取图像中特征点,并对提取出的特征点进行预匹配,然后再利用RANSAC算法消除误差较大的误匹配。实验结果表明基于RANSAC的PCA-SIFT具有良好的匹配效果且速度和效果都优于SIFT算法。
2. PCA-SIFT算法
PCA-SIFT算法是SIFT算法的改进算法,将传统SIFT算法中的直方图法换做主元分析法 [6] ,降低了传统SIFT特征描述符的维数,减少了数据量,提高了匹配效率。PCA-SIFT算法需要如下几个步骤:1) 多尺度检测极值点;2) 计算关键点特征方向;3) 生成特征描述子。
2.1. 多尺度极值点检测
根据文献 [7] ,尺度变换中把高斯卷积核当作唯一的变换核,并且也是作为唯一的线性核,一幅二维图像在不同尺度空间下的尺度可表示为:
 (1)
(1)
 (2)
(2)
其中,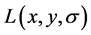 定义为原始图像
定义为原始图像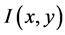 与一个可变尺度的2维高斯函数
与一个可变尺度的2维高斯函数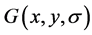 卷积运算。
卷积运算。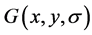 是尺度可变的高斯函数,
是尺度可变的高斯函数,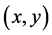 是空间坐标。
是空间坐标。
特征点的检测要在尺度空间和平面空间中同时进行,这样才可以确保得到稳健性强的特征点。因此就引入了DoG算子,它是两个不同尺度高斯核的差分值 [8] ,DoG算子的构成为:
 (3)
(3)
构建一个大小为O组,并且每组有S层的高斯金字塔,在组内相邻的高斯图像差分得到高斯差分图像。在高斯差分图像中检测极值点,在每一幅高斯差分图像中的每一个像素点,和它所在图像的八领域像素比较,而且要和它所在图像的上一层和下一层的各九个邻近的像素点比较。为了获得稳定的特征点,将不稳定的点除去,不稳定的点包括低低对比度的点和边缘上的点。可以利用 去除低对比度的点。
去除低对比度的点。
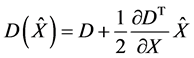 (4)
(4)
其中 绝对值小于0.03的极值点都将被丢弃。利用如下公式
绝对值小于0.03的极值点都将被丢弃。利用如下公式
 (5)
(5)
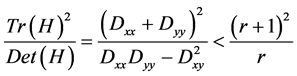 (6)
(6)
其中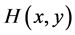 是Hessian矩阵,除去边缘上的点。通过上述过程就得到稳定的特征点。
是Hessian矩阵,除去边缘上的点。通过上述过程就得到稳定的特征点。
2.2. 计算特征点方向
为了使关键特征具有旋转不变性,采用相对的概念为关键点赋一个方向,定义的关键点描述子是相对这个方向的。对于L上的每一个点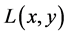 ,计算梯度和方向:
,计算梯度和方向:
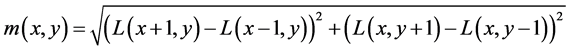 (7)
(7)
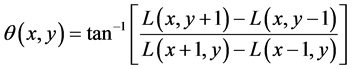 (8)
(8)
以关键点为中心,划定一个区域,利用所在区域内的点的梯度形成一个直方图。直方图的横坐标是梯度方向,纵坐标是梯度大小,对于归到横坐标上的点,将其梯度大小相加,其和作为纵坐标。将直方图中纵坐标最大的一项的方向作为关键点的主方向,如果存在其他方向,纵坐标的大小大于主方向纵坐标大小的80%,将其作为关键点的副方向。
2.3. 生成特征描述子
至此已经为关键点赋予了图像位置,方向以及尺度,这一步根据关键点周围的局部特征计算一个描述子。如图,以特征点为中心,选取一个 的区域,再将其平均分成4个
的区域,再将其平均分成4个 的小区域,计算每个小区域的梯度直方图,直方图包涵8个bin方向,这样就获得了一个
的小区域,计算每个小区域的梯度直方图,直方图包涵8个bin方向,这样就获得了一个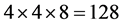 维的向量,也就生成了特征描述符向量(如图1 SIFT描述子的生成)。
维的向量,也就生成了特征描述符向量(如图1 SIFT描述子的生成)。
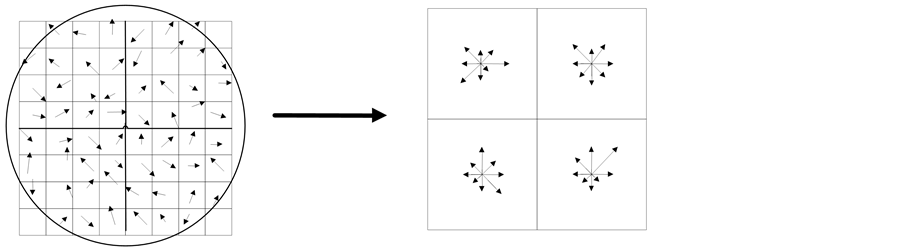
Figure 1. Generation of SIFT descriptor
图1. SIFT描述子的生成
用主元分析法对128维SIFT描述子降维的过程如下:首先将两幅待匹配图像中所有n个特征点描述子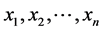 作为样本,构成一个
作为样本,构成一个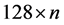 矩阵C。然后计算矩阵C的均值向量
矩阵C。然后计算矩阵C的均值向量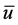 和
和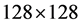 的协方差矩
的协方差矩
阵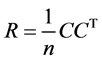 的
的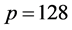 个特征值
个特征值 和特征向量
和特征向量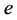 。并将特征值按从大到小顺序排列,则有
。并将特征值按从大到小顺序排列,则有
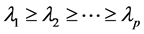 和对应的特征向量
和对应的特征向量 。选选出对应最大K个特征值的特征向量作为主成分方向。本文选取K = 36,最后构造一个
。选选出对应最大K个特征值的特征向量作为主成分方向。本文选取K = 36,最后构造一个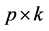 的矩阵
的矩阵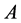 。将原始128维描述子按照公式投影到这个K维子空间,得到描述子的主成分表示
。将原始128维描述子按照公式投影到这个K维子空间,得到描述子的主成分表示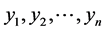
 (9)
(9)
3. RANSAC算法
RANSAC算法 [9] 的基本假设是样本中包含正确数据也包含异常数据。而PCA-SIFT算法中的异常数据则是进行预匹配所产生的错误匹配或者误差较大的匹配。利用RANSAC算法消除误匹配,采用如下思想:
1) 考虑一个最小抽样集视为n的模型(n为初始化模型参数所需的最小样本数)和一个样本集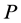 ,集合
,集合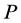 的样本数
的样本数 ,从
,从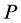 中随机抽取n个样本,构成
中随机抽取n个样本,构成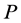 的子集
的子集 ,用来初始化模型M。
,用来初始化模型M。
2) 余集 中与模型M的误差小于某一设定阈值
中与模型M的误差小于某一设定阈值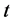 的样本集合和集合
的样本集合和集合 构成集合
构成集合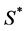 。
。 是内集,它们构成
是内集,它们构成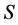 的一致集。
的一致集。
3) 若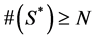 ,认为得到正确的模型参数,并利用集
,认为得到正确的模型参数,并利用集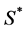 (内点),采用最小二乘等方法重新计算新的模型
(内点),采用最小二乘等方法重新计算新的模型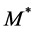 。重新随机抽取新的
。重新随机抽取新的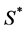 ,重复以上过程。
,重复以上过程。
4) 在完成一定的抽样次数后,若未找到一致集,则算法失败,否则选取抽样后得到的最大一致集判断内外点,算法结束。
4. PCA-SIFT的优化算法
本文PCA-SIFT算法提出了一种改进的图像立体匹配算法,具体步骤如下:
Step1构建高斯差分金字塔并检测极值点,经过稳定性筛选出关键点;
Step2利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,将坐标轴旋转为关键点的主方向;
Step3利用主元分析法生成32维特征描述子;
Step4按照最近邻比率算法对图像进行匹配,得到N对匹配点并以最近邻比率的大小进行排序;
Step5利用RANSAC算法进行变换矩阵参数的拟合,最后用得到的矩阵模型剔除错误匹配点。
5. 实验结果
实验环境为CPU 2.20 GHz,内存8.00 GB,显存2.19 GHz,操作系统为Windows 10,仿真平台为Visual Studios 2010+Opencv2.4.10,所用的图像采集设备为Bumblebee双目视觉相机。使用了多幅图像进行实验,为了验证算法的有效性,将不同算法做实验比较,并对结果进行分析。在实验中对SIFT、PCA-SIFT、PCA-SIFT+RANSAC的性能进行了对比分析。实验结果图如图2~4所示。
根据表1,表2可以得知,PCA-SIFT在匹配时间上要优于SIFT算法,在图片中存在大量的匹配点,这个优点尤为突出;但是PCA-SIFT的误匹配要高于SIFT算法,采用RANSAC应用在PCA-SIFT算法上后,误匹配率降低,且低于SIFT算法,时间上还优于SIFT。综上诉述,PCA-SIFT + RANSAC算法在时间上和匹配效果上优于SIFT算法。

Figure 3. PCA-SIFT matching results
图3. PCA-SIFT匹配结果图

Figure 4. PCA-SIFT + RANSAC matching results
图4. PCA-SIFT + RANSAC匹配结果图
表1. 实验图数据

Table 2. Multiple sets of experimental data
表2. 多组实验数据
6. 结语
从上述理论分析和实验结果可以看出,基于RANSAC和PCA-SIFT算法的方法能够满足较高精度,同时使匹配的复杂度大大降低,算法在实时性和准确性方面得到了显著的提高。由上述算法的分析可以知:SIFT算法和PCA-SIFT算法具有相同的特征点坐标,方向,梯度,不同之处在于周围描述子不同,SIFT算法采用128维,而PCA-SIFT算法利用PCA降维达到32维,在后期匹配上,PCA-SIFT算法将会节省大量时间。利用RANSAC消除误匹配,又使PCA-SIFT算法在匹配效果上得到优化。采用基于RANSAC的PCA-SIFT的特征匹配,在保证匹配结果有效性和准确性的同时,极大提高了匹配效率和运算速度。