摘要:
基于逐次截尾数据，在复合Mlinex对称损失下，研究BurrXII分布形状参数和失效率的Bayes估计，并证明了其容许性。
Abstract:
In this paper, we discuss the Bayesian estimation of the shape parameter and the failure rate from BurrXII distribution, under composite Mlinex loss function and progressive type-II censoring samples, we got the general expression and exact expression of the Bayesian estimation, and we also proved that the Bayesian estimation was admissible.
1. 引言
BurrXII分布是精算师较常用分布的之一，它在经济科学、保险精算学和环境科学等众多领域内有广阔的应用。该分布的失效率函数可类似于对数正态分布和逆高斯等分布某些特性，譬如：都不是单调函数。其分布已在质量控制和可靠性理论中均得到了广泛的应用，因此对BurrXII分布性质亟需进行深入的探讨，将具有较为重要的现实意义，从而引起了越来越多的研究者的关注。至今，很多学者开始致力于这方面的研究，例如：文献 [1] 分别在完全数据和删失数据情形下，获得了参数的极大似然点估计和区间估计；文献 [2] 针对删失数据，采用线性指数损失函数，得到了参数的经验Bayes估计；文献 [3] 研究了该分布的统计推断问题；文献 [4] 探讨了熵损失下参数的Bayes估计。本文在此基础上，将基于定数截尾样本和复合Mlinex对称损失下，研究BurrXII分布中形状参数和失效率函数的Bayes估计，并讨论其容许性。
设随机变量X服从BurrXII分布，其分布函为
, 
, 
,
.
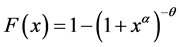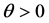显然，参数
已知时，在给定形状参数
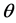的条件下，随机变量X的条件概率密度为
, 
, 
,
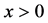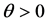(1)
若随机变量X表示产品寿命，易知产品的失效率为
,
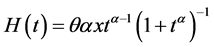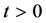(2)
定义1.1 [5] 记Mlinex非对称损失函数为：
, 
, 
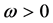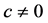
其中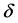
是未知参数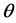
的判别空间的一个估计，则称损失函数
, 
,
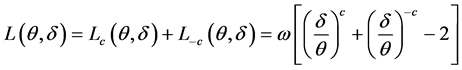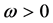(3)
为复合MLinex对称损失函数。
易知此损失函数为对称的非负严格凸损失函数，当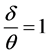
时，损失函数取得最小值0。若令
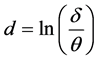，则(3)可表示为复合Linex对称损失；若令
，则(3)即为q-对称熵损失。
2. 逐次截尾试验
若n个独立且都服从BurrXII分布的部件进行寿命试验，未失效的部件可在失效时刻前被移离试验，即当观察到n个部件中有1个部件失效时，记失效时刻为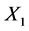
，此时从剩余的
个部件中任取出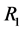
个移离试验，其余
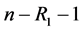个继续工作，以此类推，当正在工作的
个部件中又有一个部件失效时，记失效时刻为
，同时从
个部件中任取
个移离试验，其余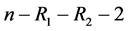
个部件继续工作。依此类推，试验进行到第
个部件失效，记失效时刻为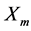
，此时剩余的
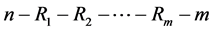个全部退出，试验终止。其中
是事先给定的。根据上述实验，
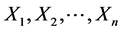为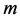
次观测得到的失效时间，由文献 [6] 知，在
已知的条件下，其联合概率密度为
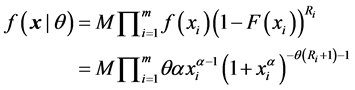(4)
其中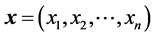
，
3. Bayes估计
在Bayes统计中，参数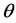
是随机变量而它的先验分布往往未知，一般可利用历史样本采用经验Bayes，获得
的经验Bayes估计。本文将采用Jeffreys原则获得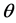
的先验分布。
由(4)式可知，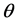
的对数似然函数为
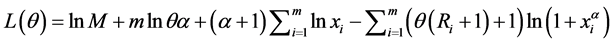
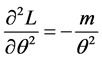
可得
的Fisher信息量
，故参数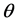
的先验分布可取为
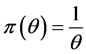(5)
引理3.1 [7] ：在给定的Bayes决策问题中，(1)若损失函数
关于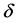
为严凸函数，则该统计判决问题的Bayes解几乎处处唯一。
(2)假如对给定的先验分布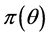
，
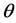的Bayes估计是唯一，则它是容许的。
定理3.1：在模型(1)和复合Mlinex对称损失(3)下，若在判别空间中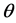
存在估计量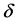
，其Bayes风险
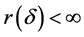，则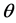
对任意给定的先验分布
有唯一的Bayes估计
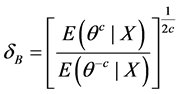
证明：在损失(3)下，
对应的Bayes风险为
要使得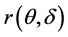
达到最小，只需
达到最小即可。
而
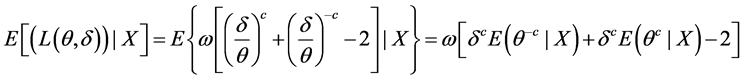
记
要使得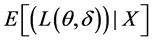
达到最小，只需
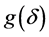几乎处处达到最小。
令
关于
求导等于零，可得
由于
是凸函数，故
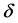是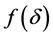
的唯一最小值点，即证。
定理3.2 假设参数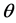
先验分布为(5)，在损失(3)下，BurrXII分布的形状参数
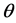的唯一的Bayes估计
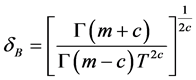，且它是容许的，其中
。
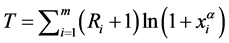证明：因为先验概率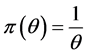
，由(4)可得后验概率
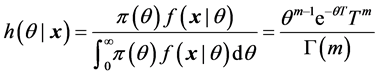
因此
的后验分布是
，其中
。
由于
由定理3.1可得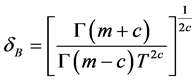
。
再证其可容许性。由引理3.1和定理3.1，由于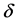
是唯一Bayes估计，易知该估计是容许的。证毕。
定理3.3 假设参数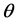
先验分布为(5)，在损失(3)下，BurrXII分布的失效率
的Bayes估计 
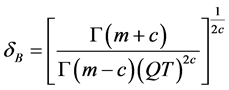,且它是容许的，其中
，
. 证明：由(2)式知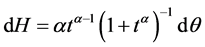
因为
所以
，
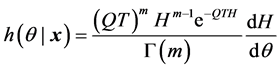从而
，
。
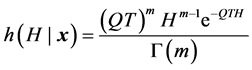于是
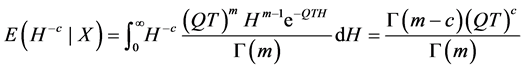
由定理3.1可得失效率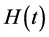
的Bayes估计
。
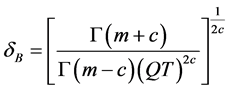同样根据引理3.1和定理3.1，由于
是唯一Bayes估计，易知该估计是容许的。证毕。
基金项目
国家社科基金资助项目(15BTJ031)。