1. 引言
2013年12月14日,嫦娥三号(CE-3)在月球表面实现软着陆,这是1976年后人类探测器首次落月探测,对人类科学考察月球资源、环境具有重大意义 [1] - [3] 。
CE-3的软着陆过程是指CE-3从近月点降落到月面的过程,共分为6个阶段(图1):
1) 主减速段:从距离月面15 km减少到3 km,实现CE-3减速;
2) 快速调整段:距月面3 km到2.4 km,在2.4 km处将水平速度减为0 m/s,期间调整姿态,使发动机推力竖直向下;
3) 粗避障段:距月面2.4 km到100 m,主要避开大的陨石坑,拍照获得数字高程图,并初步确定落月地点;
4) 精避障段:距月面100 m到30 m,CE-3拍照获得数字高程图,确定最佳着陆地点;
5) 缓速下降段:距月面30 m到4 m,实现在距月面4 m处速度降为0 m/s;
6) 自由落体段:距月面4 m到月面,此阶段CE-3关闭发动机,自由落体到精确的落月点。
以上6个阶段的研究方法都不尽相同,其中主减速段和快速调整段主要实现了CE-3减速和姿态调整,使CE-3基本调整到预定着陆点上方,因此对这两个阶段的研究是对整个软着陆过程研究的关键内容。目前对软着陆过程的研究中,和兴锁等 [4] 给出最优推力控制方向的计算公式,周净扬等 [5] 将问题转化为两点边值问题,利用Pontryagin极大值原理,得到发动机推力的最优控制律。还有多名学者 [6] 利用Simulink
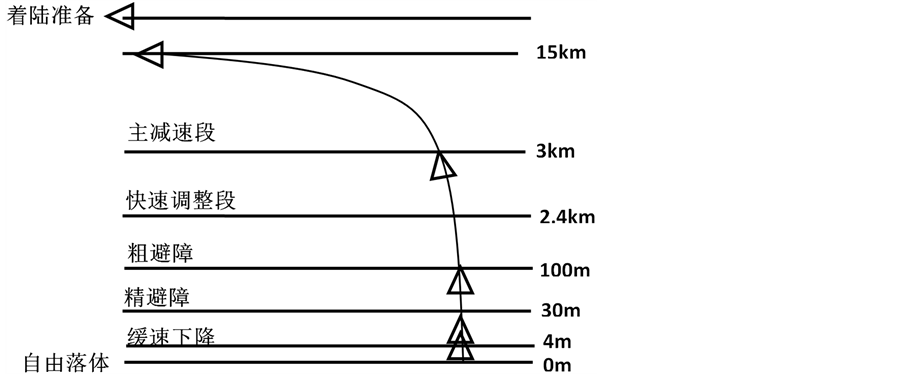
Figure 1. Chang’e-3 soft landing process
图1. 嫦娥三号月球软着陆过程示意图
软件进行轨迹仿真,等等。这些方法都是针对软着陆整体过程进行研究的,忽略了软着陆不同阶段研究方法不尽相同的事实,没有对主减速段和快速调整段的进行专门研究。
本文针对CE-3软着陆的主减速段和快速调整段,基于牛顿第二定律,燃耗最优原则,建立起这两个阶段CE-3的数学模型,给出针对两个阶段的最优控制策略。
2. 最优控制策略研究
最优控制策略是指达到燃耗最少、轨道与实际最相符这两个目标的控制策略。文献 [7] 指出主减速段和快速调整段CE-3不仅受月球引力,而且也受自身多台发动机的推力。推力方向和大小会随实际需要做微小调整,引力方向和大小也会随着CE-3轨迹的变化有微小变动。为了简化问题,在实际情况允许的范围内,本文做出如下假设:
(A1) 嫦娥三号在软着陆的主减速段和快速调整阶段的受力状态相同;
(A2) 在主减速和快速调整阶段发动机推力f方向恒定,大小可变;
(A3) 月球对CE-3的引力恒定(即:CE-3所受重力恒定);
(A4) 不考虑月球自转对轨迹的影响。
文献 [7] 指出CE-3在主减速阶段的开始点速度方向水平,大小为近月速度。故这两个阶段CE-3做初速度水平,受恒力的类平抛运动,且水平方向CE-3所受合力方向与初速度方向相反,竖直方向CE-3所受合力指向月球。
由假设(A1)~(A4)和以上的分析,主减速段和快速调整段CE-3的受力分析见图2。
图中发动机推力大小为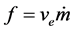 ,该力与水平方向夹角为
,该力与水平方向夹角为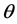 ,
,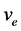 是比冲(单位米/秒),
是比冲(单位米/秒),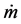 是单位时间燃料消耗(单位:公斤)。
是单位时间燃料消耗(单位:公斤)。
由牛顿第二定律,对CE-3的受力沿水平x方向和竖直y方向分解,分别取水平向右和竖直向下为水平、竖直方向的正方向,有如下结果:

式中 是CE-3的质量,随时间间
是CE-3的质量,随时间间 的增大而减少。
的增大而减少。
整理得:
根据假设(A2),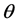 方向不变。取
方向不变。取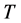 为经历这两个阶段共需要的时间,在区间
为经历这两个阶段共需要的时间,在区间 上,沿x方向两次对
上,沿x方向两次对 积分,有
积分,有
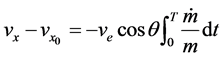
式中,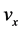 为水平末速度0,
为水平末速度0,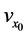 为水平初速度
为水平初速度 (
(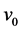 方向与正方向相反,故符号取负),由此得
方向与正方向相反,故符号取负),由此得
 (1)
(1)
式中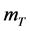 表示这两个阶段结束后CE-3的质量,即:CE-3的剩余质量。
表示这两个阶段结束后CE-3的质量,即:CE-3的剩余质量。
在区间 上,沿y方向两次对
上,沿y方向两次对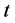 积分,并用
积分,并用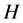 表示这两个阶段的高度差,即
表示这两个阶段的高度差,即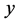 从0时刻的高度到
从0时刻的高度到

Figure 2. Force analysis of Chang’e-3 in the main reduction phase and quick adjustment phase
图2. 嫦娥三号在主减速阶段和快速调整阶段受力分析
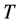 时刻的高度变化(高度由高降到低的变化),有
时刻的高度变化(高度由高降到低的变化),有
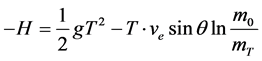
即:
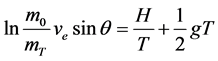 (2)
(2)
将式(1)平方后与式(2)平方后相加,得:
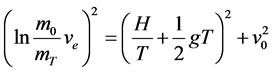 (3)
(3)
由于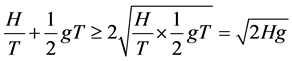 ,所以使等式右端取值最大的
,所以使等式右端取值最大的 值为
值为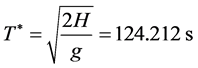 ,此时嫦娥三号剩余质量
,此时嫦娥三号剩余质量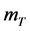 最大,为
最大,为
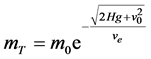 (4)
(4)
式(4)就是针对主减速段和快速下降段所建立的燃耗最优模型。
3. 相关数据和参数的选取和计算
根据文献 [7] ,相关参数取值为:初始速度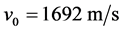 ,初始质量
,初始质量 ,发动机比冲
,发动机比冲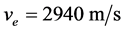 ,主减速和快速下降段的高度差
,主减速和快速下降段的高度差 ,月球表面重力加速度
,月球表面重力加速度 。
。
代入参数值到模型(4)中,求出最大剩余质量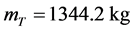 。
。
此时,嫦娥三号的推力为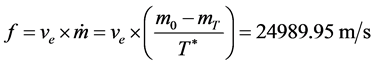 。根据假设(A2),该力为恒力,水平分力为
。根据假设(A2),该力为恒力,水平分力为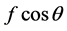 亦为恒定值,所以水平方向可以看做速度由
亦为恒定值,所以水平方向可以看做速度由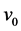 减为0的匀减速运动,加速度
减为0的匀减速运动,加速度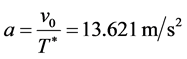 ,由
,由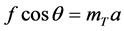 ,得
,得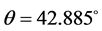 。
。
故主减速和快速调整段的最优控制策略是发动机推力大小恒为24989.95 N,方向与轨迹方向相反且与水平方向夹角为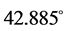 。
。
4. 敏感性分析和误差检验
根据上述研究结果,主减速阶段和快速调整阶段建立的数学模型是式(4)。在该模型中,取月球表面重力加速度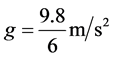 ,比冲
,比冲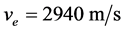 ,主要讨论燃料初始质量
,主要讨论燃料初始质量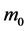 、主减速段初至快速调段末的高度差
、主减速段初至快速调段末的高度差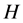 、近月点的速度
、近月点的速度 三者在它们的估计值附近存在微小变化时对问题结论的影响 [8] 。
三者在它们的估计值附近存在微小变化时对问题结论的影响 [8] 。
① 初始速度
固定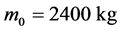 ,
, ,分析
,分析 的变化对最终剩余质量的影响,这时模型1变为
的变化对最终剩余质量的影响,这时模型1变为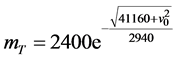 。
。
令参数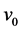 在估计值1962上下各改变1%和5%,计算剩余燃料质量,数值结果见表1。
在估计值1962上下各改变1%和5%,计算剩余燃料质量,数值结果见表1。
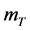 随参数
随参数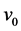 变化的敏感度,记为
变化的敏感度,记为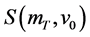 。代入相关参数值,模型(4)为:
。代入相关参数值,模型(4)为:
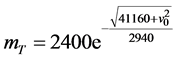
在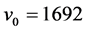 时,
时,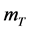 关于
关于 的敏感度为:
的敏感度为:

它表明初始速度每降低1%将导致剩余燃料质量增加0.571%,表明剩余燃料质量对初始速度的敏感性很低。
② 垂直高度
固定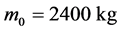 ,
,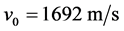 ,分析
,分析 的变化对
的变化对 的影响。令参数
的影响。令参数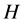 在估计值
在估计值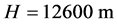 上下各改变1%和5%,分别估计剩余燃料质量,数值结果见表2。
上下各改变1%和5%,分别估计剩余燃料质量,数值结果见表2。
此时高度差与剩余燃料质量的关系为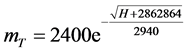 ,所以在
,所以在 附近,H关于
附近,H关于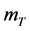 的灵敏度为:
的灵敏度为:

结果表明,高度差每增加1%,剩余燃料的质量减少0.0048%,表明剩余燃料质量对高度差的敏感性非常低。
③ 初始质量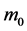
固定主减速阶段 、
、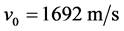 ,分析
,分析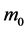 的变化对
的变化对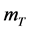 的影响。此时,模型为
的影响。此时,模型为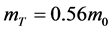 ,令参数
,令参数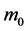 在估计值 2400 上下各改变1%和5%,分别估计剩余燃料质量,得到数值如表3。
在估计值 2400 上下各改变1%和5%,分别估计剩余燃料质量,得到数值如表3。
此时CE-3初始质量与剩余质量的关系为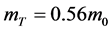 ,所以在
,所以在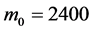 附近,
附近, 。
。
关于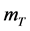 的灵敏度为:
的灵敏度为:
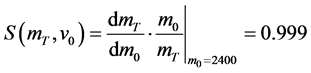
结果表明,飞船初始质量每增加1%,剩余燃料的质量增加0.999%,说明剩余燃料质量对初始质量

Table 1. Sensitivity analysis of initial velocity v0
表1. 初始速度v0敏感性分析

Table 2. Sensitivity analysis of vertical height H
表2. 垂直高度H敏感性分析

Table 3. Sensitivity analysis of initial mass m0
表3. 初始质量m0敏感性分析
的敏感性非常低。
另外,模型1所得结论合理,和文献 [7] 相关结论吻合,可认为误差比较小,相关结论是可靠的。
本文误差主要产生在假设部分,假设(A2)认为发动机推力f方向恒定,实际操作中f方向是有微小变化的,故产生误差。具体误差大小还要在以后继续进行研究。
5. 结论
本文针对嫦娥三号主减速和快速下降这两个飞行阶段,忽略了非重点因素的影响,提出适当合理的假设,构建了理论模型来解决燃耗最优问题。模型得出的最终结果与实际资料相吻合,误差及敏感性分析的结果表明计算结果是可以接受的。但是,本文在忽略了其它阶段的研究,其进一步的工作还需要在将来的研究中继续进行。
基金项目
本文受到西北农林科技大学基本科研业务专项资金资助(No. 2014YB023),西北农林科技大学博士科研启动项目资助(No.Z109021414),西北农林科技大学本科优质课程建设项目资助(数学模型)及西北农林科技大学教改项目资助(No.JY1504078)。