1. 引言
非线性现象出现于非线性系统中的某些特殊动力学行为,是非线性系统中独有的反映其运动本质的一类现象,在线性系统中是见不到的,也不能用线性系统的理论来解释。近几年来,非线性现象的研究已经广泛的存在于物理学、力学、应用数学等多个学科领域中。
非线性发展方程是刻画非线性现象的一种重要工具,截止目前,非线性发展方程的精确解构造问题引起了人们的广泛关注,已经有很多不同类型的非线性发展方程出现在数学和物理科学领域,很多专家学者在如何求解非线性方程的精确解方面做了大量有效的工作,构造出多种有效的求解方法,如齐次平衡法 [1] ,Tanh函数法 [2] ,Hirota双线性方法 [3] ,Bäcklund变换法 [4] [5] ,反散射法 [6] ,Darboux变换法 [7] 等。
本文主要研究如下KdV型方程的精确解:
 (1.1)
(1.1)
在文 [8] 中,我们采用了指数函数方法求解KdV方程,得到了KdV方程的6种不同形式的指数函数解。然而由于求解非线性波动方程并没有统一适用的方法,因此继续寻找一些能够构造出方程(1.1)新精确解的方法是十分必要的。因此,在本文中,我们主要应用了F-展开法求解KdV方程。
本文的内容安排如下:第二节简单介绍了F-展开法的主要思想。第三节利用F-展开法研究方程(1.1),得到了3组Jacobi椭圆函数解,并画出对应的图像,观察波的传播状况。最后一节是对本文内容的一个总结。
2. 方法概述
本文以如下的非线性偏微分方程
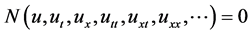 (2.1)
(2.1)
为例来简单阐述一下F-展开法的主要思想。在方程(2.1)中,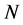 为其变元的多项式,并包含非线性项和高阶偏导数项。
为其变元的多项式,并包含非线性项和高阶偏导数项。
1) 假设方程(2.1)具有行波解:
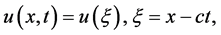 (2.2)
(2.2)
则方程(2.1)可转化为:
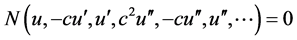 (2.3)
(2.3)
2) 假设方程(2.3)可表达成如下形式:
 (2.4)
(2.4)
其中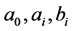 为常数,而函数
为常数,而函数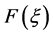 满足如下方程:
满足如下方程:
 (2.5)
(2.5)
其中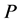 ,
,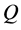 ,
,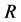 为常数。在此方程中,如果给
为常数。在此方程中,如果给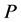 ,
, ,
,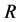 以具体数值,那么可得到
以具体数值,那么可得到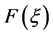 的具体形式(表1中为
的具体形式(表1中为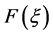 的部分解)。
的部分解)。
3) 将(2.4)、(2.5)带入到方程(2.3)中,然后平衡方程(2.3)的非线性项和最高阶导数项即可确定表达式(2.4)中的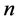 。
。
3. 方程求解
本节主要采用上述F-展开法来求解方程(1.1),对于该方程,把 带入到方程(1.1)中,可得:
带入到方程(1.1)中,可得:
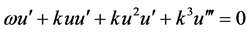 (3.1)
(3.1)
假设方程 具有(2.4)的形式的解,即
具有(2.4)的形式的解,即
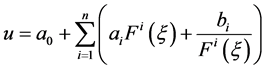 (3.2)
(3.2)
其中,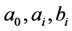 为待定系数,函数
为待定系数,函数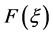 满足如下形式:
满足如下形式:
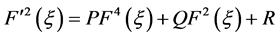 (3.3)
(3.3)
通过方程(3.3),我们可得:
(3.3)的一阶导数为:
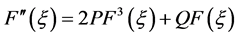 (3.4)
(3.4)
(3.3)的二阶导数为:
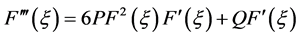 (3.5)
(3.5)

Table 1. Relations between the coefficients and corresponding in
表1. 系数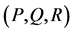 之间的关系及满足方程
之间的关系及满足方程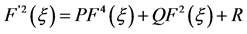 的
的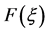
现在,为了确定方程(3.2)中系数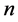 的具体数值,我们将(3.2)代入到(3.1)中,并借助方程(3.4)、(3.5),可得:
的具体数值,我们将(3.2)代入到(3.1)中,并借助方程(3.4)、(3.5),可得:
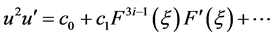 (3.6)
(3.6)
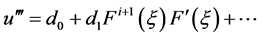 (3.7)
(3.7)
此时,平衡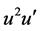 和
和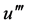 的非线性项和最高阶导数项可得
的非线性项和最高阶导数项可得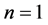 ,即:
,即:
 (3.8)
(3.8)
之后,借助Mathematica软件求解这个方程组,得到如下几种形式的解。
情形1:当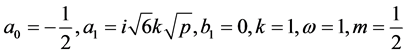 时,方程为:
时,方程为:
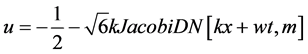 (3.9)
(3.9)
其图像如图1所示。
情形2:当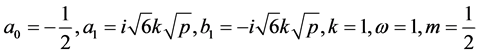 时,方程为:
时,方程为:
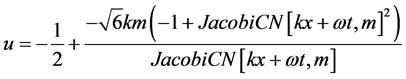 (3.10)
(3.10)
其图像如图2所示。
情形3:当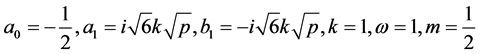 时,方程为:
时,方程为:
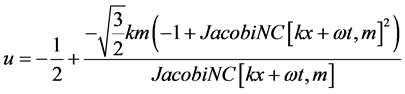 (3.11)
(3.11)
其图像如图3所示。
4. 总结
本文利用F-展开法深入系统的分析了KdV型方程的精确解,给出新的雅克比椭圆函数解,这些解能够加强对该方程的理解,从而促进该方程在数学、物理等领域的应用,因此本文的工作具有一定的理论意义和应用价值。
致谢
本文得到北京市本科生培养–大学生科研训练(市级)项目(XN001-159),北方工业大学优秀青年教师计划(XN132)、青年拔尖人才计划(XN071009)和科研创新团队建设计划项目(XNXN07005)支持。感谢项目指导教师张智勇老师的悉心指导。