1. 引言
上海证券综合指数(简称“上证综指”)反映了在上海证券交易所上市股票价格的变动情况,在我国,股票市场上最具代表性的指数之一就是上证综指,它的波动能及时准确的反映股票市场的运行情况 [1] 。文献 [2] 中将非平稳时间序列进行差分,并通过自相关系数及偏自相关系数来对模型进行识别,提出了完整的建模、估计、参数检验的方法。时间序列反映了对象的发展趋势,文献 [3] - [6] 提出了针对不同对象的建模方法。文献 [3] 以指数为对象,研究了上证综指中的ARCH现象。文献 [4] 通过建立对应的时间序列模型来研究风险溢价的时变性。文献 [5] 研究了用ARIMA模型来探究上证A股指数的变化规律。文献 [6] 提出了ARIMA模型以及相关干预模型,并结合政府对股市的重大干预,来对深圳证券交易市场成分指数进行建模。ARIMA模型具有广阔的应用空间,适用于多种领域内的预测研究,文献 [7] - [10] 研究了ARIMA模型的应用实例。文献 [7] 将生态承载能力进行量化,从而获取时间序列并通过ARIMA模型进行动态模拟和预测。文献 [8] 研究了ARIMA模型在信用风险波动性上的应用。文献 [9] [10] 研究了ARIMA与神经网络组合模型,文献 [9] 将该模型用于GDP预测,文献 [10] 则将该模型用于碳排放预测,从中可以看到,没有任何一种模型是万能通用的,不同的时间序列,甚至同一序列选择不同时间段所适合的模型是不同的。本文研究股票市场的短期预测,考虑到上证综指收盘价受很多随机因素的干扰,往往是非平稳序列,因此选择ARIMA模型对上证综指2014.5.12~2015.5.22日的收盘价格进行有效建模,再利用该模型进行实证并判断预测的好坏。
2. 建模
2.1. ARIMA模型
金融时间序列模型大都是非平稳的序列,但对于短期数据,若通过适当的差分往往能获得平稳的序列,因此本文选择常用的非平稳时间序列模型自回归求和移动平均模型即ARIMA(p,d,q)来进行预测,该模型的本质实际上是差分运算和ARMA(p,q)模型的结合。
2.1.1. 自回归模型(AR模型)
若平稳序列在t时刻的值为 ,则这个值可以表示成过去p个时刻
,则这个值可以表示成过去p个时刻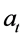 的值
的值 的线性组合加上t时刻所对应的残差
的线性组合加上t时刻所对应的残差 ,该残差为白噪声。这个序列可以用AR模型表示为:
,该残差为白噪声。这个序列可以用AR模型表示为:
 (1)
(1)
其中,c为常数, 是自回归系数,p为自回归阶数,
是自回归系数,p为自回归阶数, 为白噪声序列。
为白噪声序列。
2.1.2. 移动平均模型(MA模型)
若平稳序列在t时刻的值为 ,则这个值可以表示成过去q个时刻残差序列
,则这个值可以表示成过去q个时刻残差序列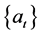 的加权平均值和
的加权平均值和 的和,且
的和,且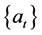 为白噪声序列,则该序列可以用移动平均模型如下表示:
为白噪声序列,则该序列可以用移动平均模型如下表示:
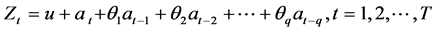 (2)
(2)
其中,u为常数, 是自回归系数,q为移动平均模型阶数,
是自回归系数,q为移动平均模型阶数, 为白噪声序列。
为白噪声序列。
2.1.3. 自回归移动平均模型(ARMA模型)
自回归移动平均过程是自回归过程和移动平均过程的组合。该模型矩阵形式如下:
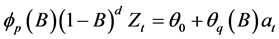 (3)
(3)
其中,p为自回归阶数,q为移动平均模型阶数,d为差分次数。
2.2. 模型选择
分析采用的数据来源于Yahoo Finance,具体为上证综指2014.5.12~2015.5.22日的收盘价格,共254个样本数据,通过分析数据特征,找到适宜模型,进行估计并预测接下来5天的收盘价格。
2.2.1. 平稳性检验
通过该指数时间序列图(图1)可以看出该时间段的序列有显著向上的趋势并伴随较小的上下波动,为非平稳序列,而从ACF图(图2)衰减缓慢可以得出,为了消除趋势,使该序列成为平稳的序列,需要对原序列进行一定阶数的差分,通过对此原序列进行平稳性检验,利用函数adf.test()检验,得到p-value = 0.9349。接下来,尝试对序列进行差分,发现2阶差分后序列的平稳性检验的p-value = 0.01,在5%的显著性水平下拒绝原假设,序列平稳。因为过度差分会损失原序列所蕴含的信息,所以,为得到平稳序列,模型取2阶差分即可,即取d = 2。
2.2.2. 白噪声检验
如果差分后的序列属于白噪声,则说明序列包含的信息中只有较少对相关研究有价值的信息,所以

Figure 1. The time series of Shanghai composite index
图1. 上证综指时间序列图
有必要对差分后的序列进行白噪声检验。本文中,我们选择Q检验,通过程序运算可得差分后的序列滞后期为10时Q检验统计量的值。所对应的p-value = 1.166e−14,远远小于0.05,表明差分后的序列包含较多的信息,为非白噪声序列,对该差分后的序列建模能提取到有价值的信息。
2.2.3. 模型定阶
选择合适的ARIMA模型,就意味着要找到合适的p,d,q,由于上面已经判断得到二阶差分后的序列为平稳序列,所以,取定d = 2。此外,还需要识别并找出合适的p和q,识别p和q阶数的方法是通过使样本ACF和PACF与已知模型的理论形态相匹配。已知模型的理论形态如表1所示。
二阶查分后差分后上证综指收盘价的ACF和PACF图如图3和图4所示。
由图3可以看出,滞后2阶自相关值基本不再超过边界值,虽然隔两个滞后期后又有2个自相关值超过边界,但是这很可能属于偶然出现的,因为理论上我们可以期望1到20之间的会偶尔超出95%的置信边界,所以,自相关值选2阶,即p = 2。另外,图4显示滞后6阶偏自相关值不再显著超过边界,虽然其中滞后4期后有1期未超过边界但之后又连续出现2次PACF值显著超过边界,所以偏自相关值选6阶,即q = 6。
综上所述,我们选定的ARIMA模型为ARIMA(2,2,6)。
3. 参数估计与检验
3.1. 参数估计
在R语言中使用arima()函数来估计模型参数,通过代码arima(data,order = c(2,2,6))可得参数估计如

Table 1. The theoretical form of model
表1. 模型的理论形态

Figure 3. ACF figure of differential series
图3. 差分后序列ACF图
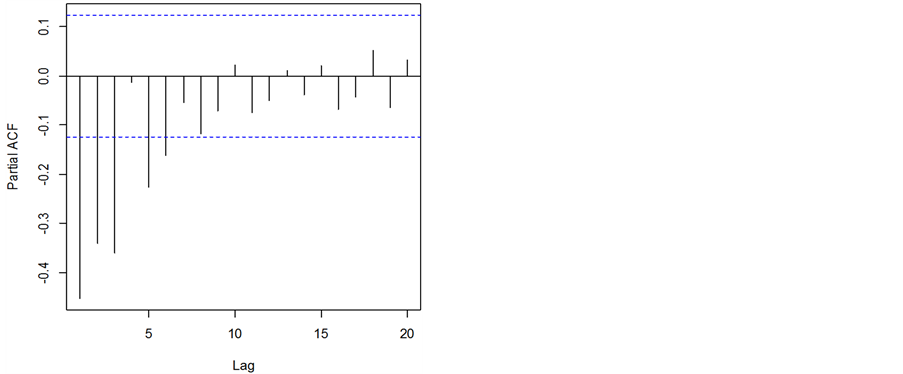
Figure 4. PACF figure of differential series
图4. 差分后序列PACF图
下表2。
所得模型如下:
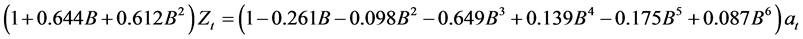
即:

3.2. 模型的有效性检验
判断模型是否有效,需要检验模型是否较充分的从原数据中提取相关的信息,一个有效的模型应该几乎提取了原数据中所包含的所有信息,使得剩下的残差序列中不再蕴含其他相关信息。这意味着残差序列应该是一个纯随机的序列,即白噪声序列。满足这样条件的模型才算是显著的有效的模型。
但需要注意的是,在检验残差时,若残差不是纯随机序列,而是由非独立的纯随机序列组合的序列,那么仅仅检验序列的纯随机性不能完全证明模型的有效性。所以,我们还需检查残差的分布,观察ARIMA
模型的预测误差是否服从均值为0且方差为常数的正态分布。与此同时,也要观察连续预测误差是否(自)相关,这主要通过直方图和QQ图来检验。
首先,通过残差ACF图来判断残差是否为白噪声序列。
如图5所示,在滞后1-20阶(lags 1 - 20)的范围内,样本自相关值都没有超出显著(置信)边界。利用R软件进行Ljung-Box检验(即Q检验),得到的p-value = 0.9978,所以可以推断在滞后1~20阶(lags 1 - 20)范围内,没明显证据说明预测误差是非零自相关的。
要判断残差是否服从均值为0,方差不变的正态分布,需要计算残差,残差直方图和QQ图如下图6和图7所示。
从图6和图7可以看出,该模型残差服从均值为0,方差恒定的正态分布。
通过上述分析,此模型的残差序列为纯随机序列,可视为白噪声,且服从均值为0,方差不变的正态分布,建立的该ARIMA (2,2,6)为有效的。
4. 模型预测与拟合
通过上述模型的检验,可以发现ARIMA(2,2,6)模型最适合样本数据的分析和预测,利用R语言中的forecast.Arima()函数对模型序列进行预测,后5个交易日上证指数的收盘价格预测如下。
由表3预测结果和真实值的比较可知,该模型具有较好的预测效果。
5. 总结
本文在历史数据的基础上建立ARIMA(2,2,6)模型并进行了上证综指日收盘价的短期预测。通过预测结果,可以看出,模型效果较好,预测结果与真实值相差较小,本文建立的模型对股票投资有着一定的建议作用。但是由于股市走势本生受很多复杂因素的干扰,且其还具有时变性、随机性和非线性等特点,

Table 2. Results of parameter estimation
表2. 参数估计结果

Table 3. The prediction of closing price
表3. 收盘价格预测
本文建立的模型仅对短期预测有效,核心在于研究特定股票大概走势。投资者可以通过走势的判断并结合对股票基本面和技术面的分析,对投资提供参考,而关于股票市场里中长期趋势的预测还有待进一步研究。