1. 引言
链传动作为机械传动中的一种重要的运动传递方式,因其经济、可靠及良好的传动性能而广泛应用于运输、采矿、冶金、军事等各种机械传动系统中 [1] 。对用于低速重载输送机一类装备的链传动,重载的链节易产生较大的拉应力,不允许链条松边的存在 [2] 。由于链传动多边形效应的存在,当主动链轮在规定条件下以最大速度转动时,会对从动链轮,链节的速度、加速度产生了影响。本文运用滑道来约束链节的运动轨迹,对不同数量负载状况下的输送链进行建模及动力学仿真。以获得链节与内外滑道之间相互作用的接触碰撞力,销轴与链轮啮合产生的冲击碰撞载荷特性。
2. U型滑道约束输送链的力特性分析
2.1. 静载荷分析
根据U型滑道约束输送链系统平衡状态,忽略过渡圆弧的轨迹变化。如图1所示;U型滑道上共有16个链节,右侧链轮为驱动链轮,左侧链轮为从动轮,两链轮的分度圆半径相等。
模型在静止状态下,链条的受力与单个链节在滑道内的位置,携带的负载数量,负载在链节的位置有关。所以确定链节在滑道上的位置对链节、滑道、链轮的受力是非常关键的。
内滑道上链节位置。在如图1所示的位置下,设链节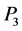 中心与竖直方向的距离为
中心与竖直方向的距离为 ,内滑道上销轴到圆心的距离为
,内滑道上销轴到圆心的距离为 ,链节
,链节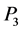 与竖直方向的夹角为
与竖直方向的夹角为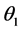 ,表示为:
,表示为:
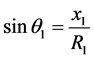 (1)
(1)
在内滑道内任意链节可表示为:
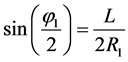 (2)
(2)
链节 ,
,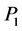 ,
,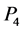 ,
,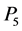 与竖直方向的夹角
与竖直方向的夹角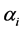 :
:
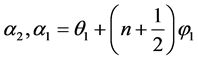
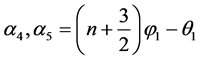 (3)
(3)
式中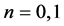 。同理,设链节
。同理,设链节 中心与竖直方向的距离为
中心与竖直方向的距离为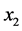 ,链节
,链节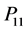 与竖直方向的夹角为
与竖直方向的夹角为 ,外滑道上销轴到圆心的距离为
,外滑道上销轴到圆心的距离为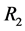 ,则有:
,则有:
 (4)
(4)
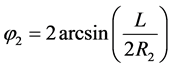 (5)
(5)
链节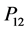 ,
, ,
,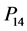 ,
,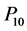 ,
,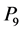 ,
,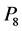 与竖直方向的夹角
与竖直方向的夹角 :
:
 (其中)(6)
(其中)(6)
2.2. 动载荷分析
U型滑道约束输送链存在多种动载荷。此系统的链条由滑道约束,故其动载荷主要由多边形效应引起的惯性载荷、链节在运动过程中受到滑道约束的冲击、销轴与链轮啮合时产生的冲击载荷,链节携带的负载数量,负载在链节中的不同位置等组成。假设链节携带的负载数量及负载所在的初始位置为已知输入条件。所以对链节在运动过程中与滑道的接触力、销轴与链轮啮合接触力的研究是非常重要的。
2.3. 接触问题求解现状
接触力在求解时,是以单向约束的问题为理论模型,用弹塑性理论来分析计算的。在发生接触的状态下,根据设定的接触刚度,以及产生的基础穿透深度来计算接触力及相关的摩擦力 [3] 。
分析系统构件在发生接触时,RecurDyn计算接触力是基于Hertz接触理论,计算基础产生的法向接触力 的公式为:
的公式为:
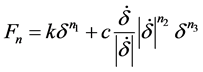 (7)
(7)
式中, 为接触刚度系数;
为接触刚度系数; 为阻尼系数;
为阻尼系数; 为接触穿透深度;
为接触穿透深度;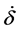 为接触穿透深度的导数(接触点的相对速度);
为接触穿透深度的导数(接触点的相对速度);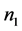 、
、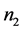 、
、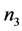 分别为刚度指数、阻尼指数、凹痕指数。
分别为刚度指数、阻尼指数、凹痕指数。
3. U型滑道约束型输送链动力学建模
3.1. 模型的建立及装配
U型滑道约束输送链模型的装配:建立一个装配体模型,载入底板、链节等,在链节部件销轴中心点与底板运动轨迹线之间添加点在线上副约束 [4] 。销轴与链轮之间添加3D约束(3D约束为碰撞接触约束,链轮和销轴碰撞时进行能量和运动的传递)。图2为链节装配结构。
3.2. 模型的简化及约束
将UG环境下建立的三维模型通过公共文件接口导入RecurDyn中。为了提高计算的效率,对模型进行简化 [5] 。RecurDyn提供了面求和功能。把两销轴圆柱面求为一体。同理把两侧内、外滑道对应部分,两端链轮,负载仓、轴承、链节板合并求和。在实际中轴承与滑道之间的摩擦鉴于滚动和滑动摩擦之间,把其简化成滑动摩擦。
在RecurDyn中提供了面面接触和扩展面—面接触约束。根据模型的要求采用扩展面—面接触约束,不仅能够提高模型的计算精度,而且有利于模型的仿真分析。
4. 机构仿真结构及分析
U型滑道约束链传动系统用于实现负载运输。链节将物品由一个位置送到预期的位置后定位停止,以便其他装备完成对该物品的卸载。模型中含有四种不同的负载,四种负载根据需要进行随机的调配,而且要求每5.5 s内,调取所需的负载。链轮要完成加速,匀速,减速三个过程的运动。假设链轮加速,减速运动的时间分别为0.5 s,匀速运动的时间为4.5 s。
根据要求,当连续两次调动相同的负载时,链轮需要在规定的时间内要转过四个链节,此时链轮,销轴,滑道受到的多边形效应及冲击载荷为最显著,所以对链节转过四个链节的情况进行仿真。
主动轮的驱动采用RecurDyn中的step函数。step函数采用三次多项式逼近海赛阶跃函数。step函数的形式为:
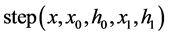
step函数中,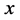 为自变量;
为自变量;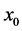 为起点自变量值;
为起点自变量值;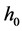 为阶跃起点处的函数值;
为阶跃起点处的函数值;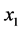 为阶跃终点自变量的值;
为阶跃终点自变量的值;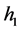 为阶跃终点的函数值。
为阶跃终点的函数值。
所以本模型中主动链轮上驱动函数为step (time,0,0,0.5,1.256) + step (time,5,0,5.5,-1.256)。
图3为模型在满负载和极限负载下的情况:满负载16个链节全部携带负载。极限负载模型,只有下滑道左侧5个链节和上滑道右侧3个链节携带负载。
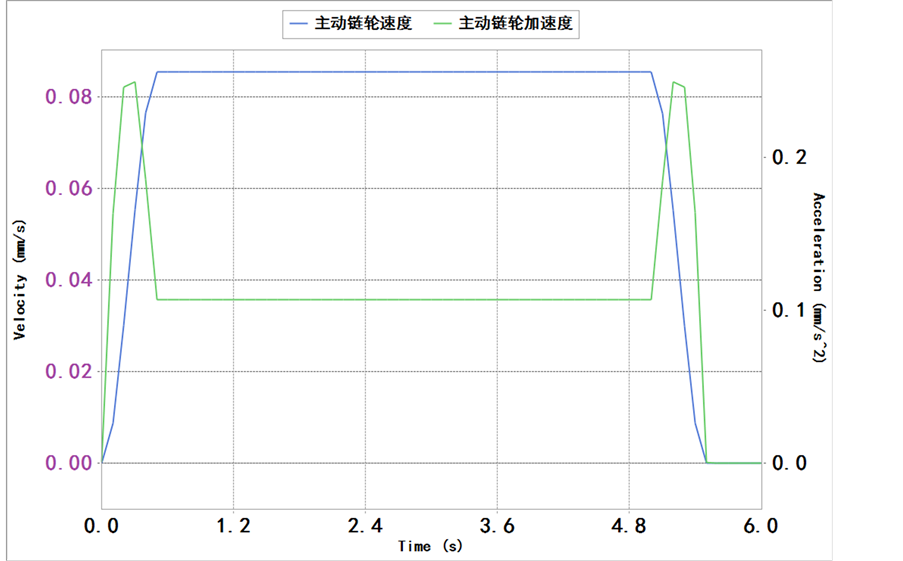
4.1. 当主动链轮以规定速度转动时,链节在携带不同负载情况下,从动链轮的速度、加速度变化
从图4主、从动链轮速度、加速度的比较可知,由于链传动多边形效应的存在,当主动链轮匀速转动时,在满负载情况下,从动链轮的速度在平均速度上下近似于正弦曲线运动,但是在极限负载情况下,其运动规律不是很明显,速度的上下波动非常明显,所以加速度曲线也明显波动。说明链节携带不同负载及负载处于不同位置对从动链轮的速度、加速产生一定的影响。
 (a)
(a) 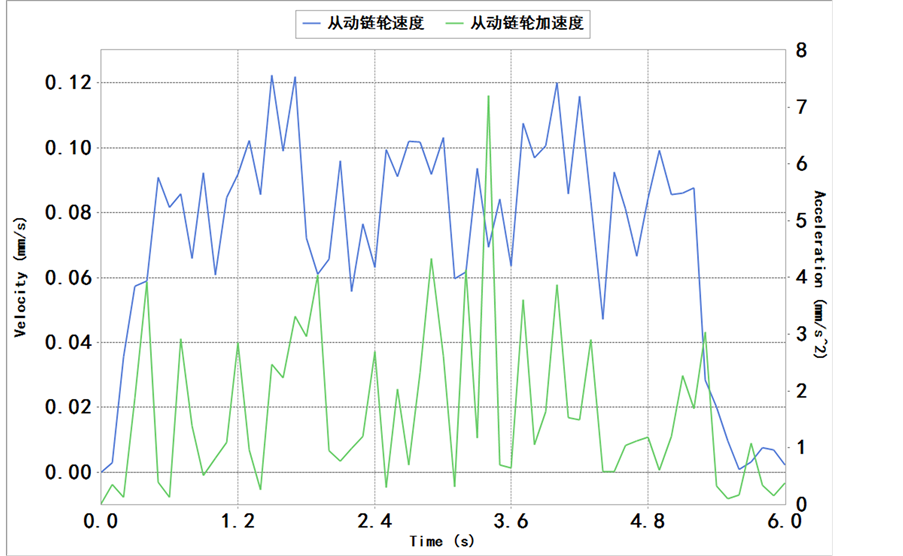 (b)
(b) (c)
(c)
Figure 4. Velocity and acceleration of the drive and passive sprocket; (a) Velocity and acceleration of sprocket; (b) Velocity and acceleration of driven sprocket with full load; (c) Velocity and acceleration of sprocket with limit load
图4. 主,从动链轮速度、加速度;(a) 主动链轮的速度、加速度;(b) 满负载下,从动链轮速度、加速度;(c) 极限负载下,从动轮速度、加速度
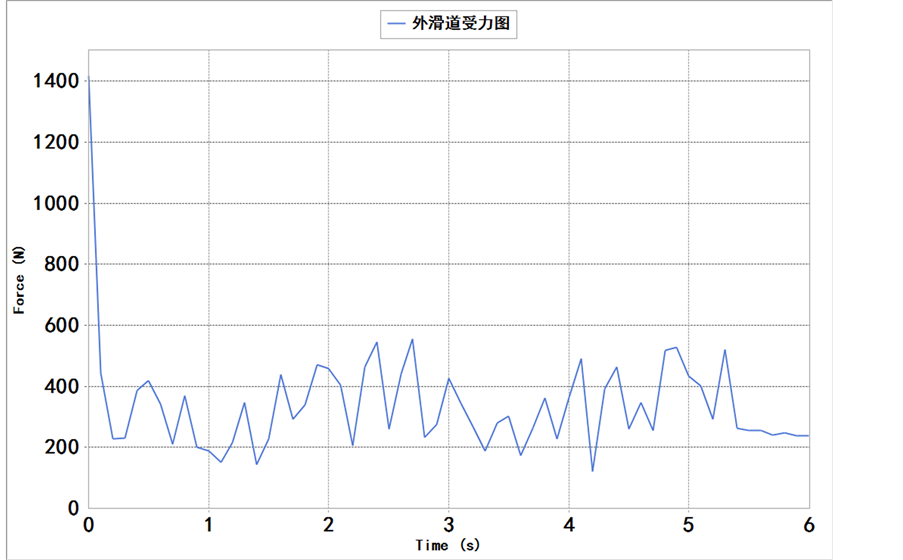
4.2. 任意链节与内、外滑道之间的接触力
从图5任意链节与内、外滑道之间的接触力比较可知,在满负载情况下,在启始加速阶段内滑道受力达到最大,在匀速运动阶段,内滑道的受力在上下波动,但是其均值基本稳定在500 N左右,最大值为730 N。在极限负载情况下,内滑道的受力出现一个明显的峰值,峰值力大约为2400 N。对外滑道的接触受力,
 (a)
(a)
 (b)
(b)
Figure 5. The contact force between the chain and slide; (a) Condition with full load; (b) Condition with limit load
图5. 任意链节与内、外滑道之间的接触力;(a) 满负载情况;(b) 极限负载情况
在满负载下,开始所受的力最大,经分析为在起始阶段,重载低速输送链的爬行现象。在稳定运行阶段,外滑道接触受力基本在300 N左右。在极限负载情况下,在某一阶段内,会出现受力峰值,经分析链节处在外滑道的最低点。在载荷相同的情况,内滑道的受力一般大于外轨道的受力,可得与滑道的曲率半径有关,曲率半径越小,链节在转动过程中速度改变越快,单位时间内受到的滑道接触碰撞力也就越显著。
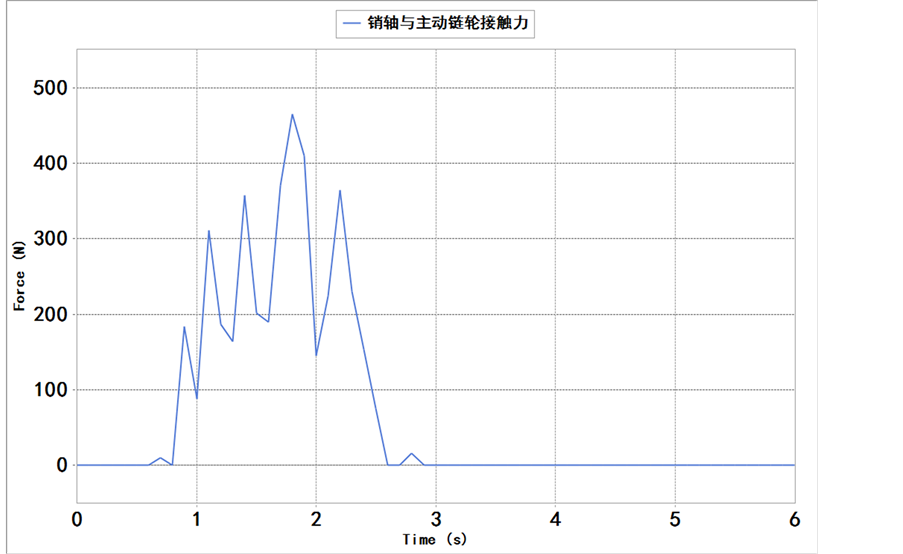
4.3.销轴与主动链轮接触时的受力
图6显示,链节在满负载情况下运动时,销轴与主动链轮的接触力在短时间内的均值,近似为正弦
 (a)
(a)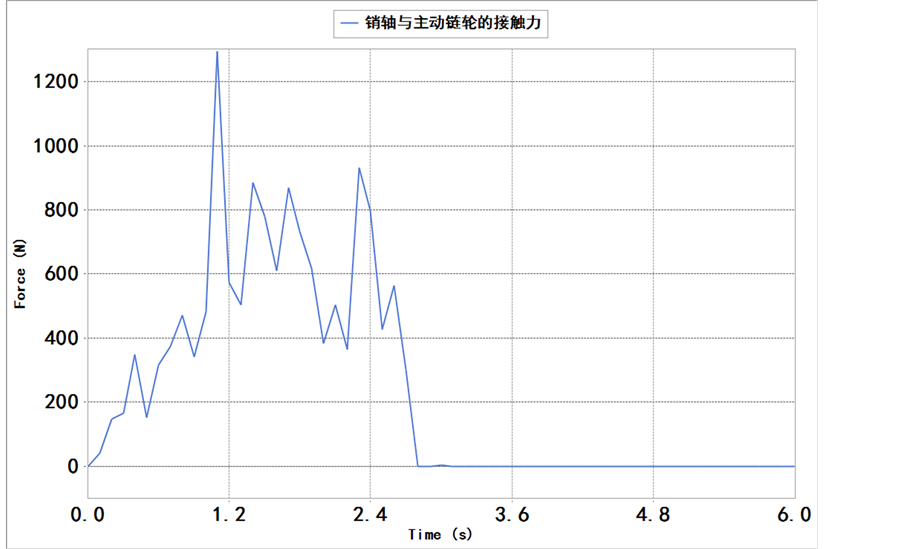 (b)
(b)
Figure 6. Pin and drive sprocket contact force; (a) Condition with full load; (b) Condition with limit load
图6. 销轴与主动链轮接触受力;(a) 满负载情况;(b) 极限负载情况
曲线。销轴与链轮的啮合:随着主动链轮的转动,受力间歇性的增长,而后再衰退。在极限负载情况下,其受力会出现突然的剧变,分析为负载的不平衡而导致的,而后又在700 N左右上下波动。
5. 结论
通过链节携带不同数量的负载及处在不同位置时,对内外滑道的受力分析,首先可知内外滑道的最大受力,为滑道尺寸的优化提供理论依据。其次,对从动链轮的运动特性分析,为传动过程中减少链传动的多边形效应提供依据。得出机构在运动中,应该尽快的补足负载,减小动载荷。通过对销轴与主动链轮接触的受力分析,为销轴的材料选择和尺寸优化提供依据。
基金项目
天津市应用基础与前言技术研究计划(13JCZDJC34100)。