1. 引言
本文我们主要考虑下述非齐次拟线性p-调和型椭圆方程
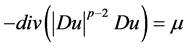 。 (1.1)
。 (1.1)
这里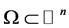 为有界开区域且
为有界开区域且 为Borel测度。
为Borel测度。
1983年,Wolff在文献 [1] 中提出了经典非线性Wolff位势。后来,Kilpeläinen,Malý [2] [3] ,Trudinger,Wang [4] 和Korte,Kuusi [5] 用不同的方法研究了拟线性椭圆方程(1.1)弱解的逐点估计
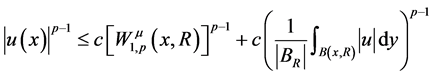 。
。
这里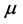 的非线性Wolff位势
的非线性Wolff位势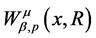 的定义如下:
的定义如下:
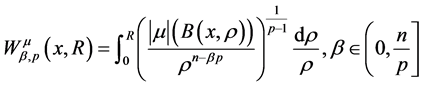 且
且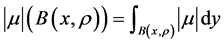 。
。
最近,Duzaar,Kuusi和Mingione在 [6] - [9] 中借助非线性Wolff位势和线性Riesz位势给出了拟线性椭圆方程(1.1)及其一般情形的弱解的逐点梯度估计。本文我们主要采用非线性Wolff位势来研究非齐次p-Laplacean方程(1.1)弱解的梯度估计,我们将结合文 [6] - [9] 的证明方法给出一个新证明。
首先,我们给出弱解的定义。若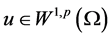 为方程(1.1)的弱解,则对任意
为方程(1.1)的弱解,则对任意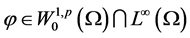 ,有
,有
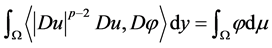 。
。
现在我们来阐述本文的主要结论。
定理1.1. 设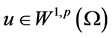 是方程(1.1)的弱解,
是方程(1.1)的弱解, ,
,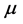 为Borel测度,且
为Borel测度,且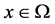 是
是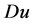 的一个Lebesgue点,
的一个Lebesgue点,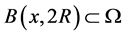 。那么存在
。那么存在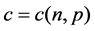 ,有如下梯度估计
,有如下梯度估计
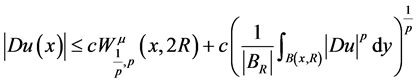 。 (1.2)
。 (1.2)
2. 主要结论的证明
我们记
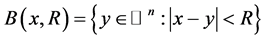 。
。
简记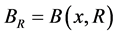 。对具有正测度的集合
。对具有正测度的集合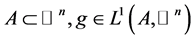 ,记积分平均
,记积分平均
 。
。
引入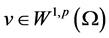 为下述参考方程的弱解
为下述参考方程的弱解
 。 (2.1)
。 (2.1)
现在我们给出齐次p-Laplacean椭圆方程(2.1)弱解的一个经典的估计(参见文献 [10] - [14] )。
定理2.1. 设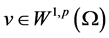 是(2.1)的弱解,则存在
是(2.1)的弱解,则存在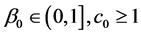 ,它们都依赖于
,它们都依赖于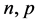 ,有如下估计
,有如下估计
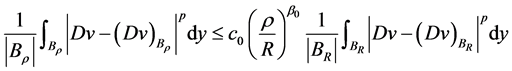 。 (2.2)
。 (2.2)
其中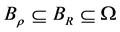 为同心球。
为同心球。
现在考虑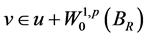 是如下Dirichlet问题的弱解
是如下Dirichlet问题的弱解
 (2.3)
(2.3)
那么,我们可以得到下面的比较引理。
引理2.2. 设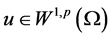 是方程(1.1)的弱解,
是方程(1.1)的弱解,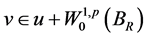 是方程(2.3)的弱解,则存在
是方程(2.3)的弱解,则存在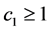 依赖于
依赖于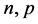 ,当
,当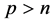 时,有估计
时,有估计
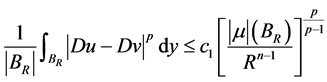 。 (2.4)
。 (2.4)
证明:我们可以通过逼近理论(见 [15] - [17] )只研究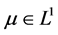 的情形。通过基本的尺度变换
的情形。通过基本的尺度变换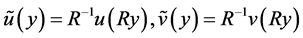 且
且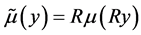
另外,通过归一化变换
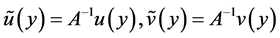 且
且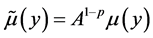 。
。
这里
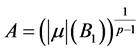 。(2.5)
。(2.5)
我们不妨假设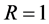 且
且 。故我们只需证明
。故我们只需证明
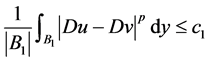 。 (2.6)
。 (2.6)
首先,由弱解的定义可得
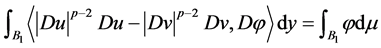 , (2.7)
, (2.7)
对任意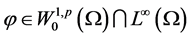 ,任意
,任意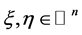 和
和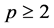 ,我们回顾以下基本不等式
,我们回顾以下基本不等式
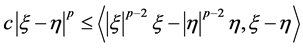 。 (2.8)
。 (2.8)
因为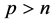 且
且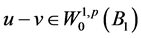 ,那么由Sobolev嵌入定理可得
,那么由Sobolev嵌入定理可得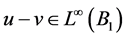 。那么取检验函数
。那么取检验函数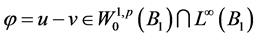 ,由(2.7)式,(2.8)式,Sobolev嵌入定理以及
,由(2.7)式,(2.8)式,Sobolev嵌入定理以及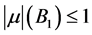 ,可知
,可知
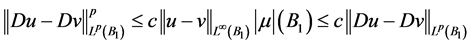 。
。
故,可得(2.6)式,所以结论得证。
下面我们记
 。
。
令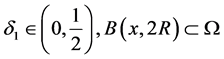 。定义
。定义
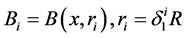 , (2.9)
, (2.9)
其中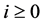 为整数。我们选取
为整数。我们选取
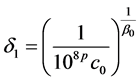 。 (2.10)
。 (2.10)
这里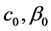 如定理2.1中的定义。
如定理2.1中的定义。
考虑 是下述Dirichlet问题的弱解
是下述Dirichlet问题的弱解
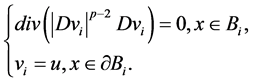 (2.11)
(2.11)
下面我们给出一个迭代引理。
引理2.3. 设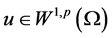 是方程(1.1)的弱解,
是方程(1.1)的弱解,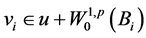 是方程(2.11)的弱解,则有下式成立
是方程(2.11)的弱解,则有下式成立
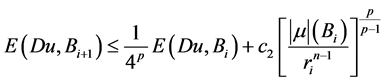 。
。
这里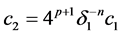 。
。
证明:由定理2.1中的(2.2)式和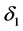 的定义式(2.10)式,可知
的定义式(2.10)式,可知
 。
。
再由引理2.2的(2.4)式和Hölder不等式,有
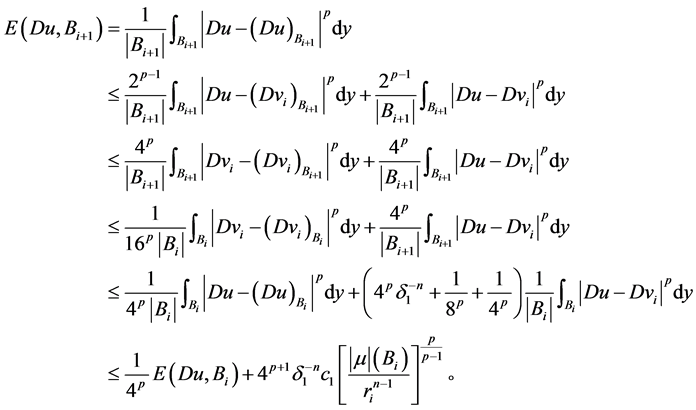
引理得证。
下面我们完成定理1.1的证明。
证明:第一步. 设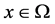 是
是 的一个Lebesgue点,
的一个Lebesgue点,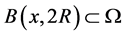 ,以下我们考虑的球都是以
,以下我们考虑的球都是以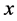 为球心的。我们选取
为球心的。我们选取
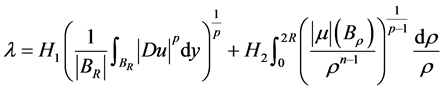 , (2.12)
, (2.12)
其中
 且
且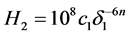 。 (2.13)
。 (2.13)
要证明定理1.1的结论,只需证明
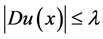 。 (2.14)
。 (2.14)
我们定义
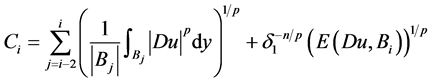 。 (2.15)
。 (2.15)
其中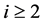 为整数。对
为整数。对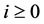 我们有
我们有
 , (2.16)
, (2.16)
由 的选取,可知对
的选取,可知对 有下式成立
有下式成立
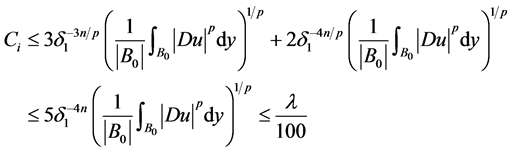 (2.17)
(2.17)
又因为
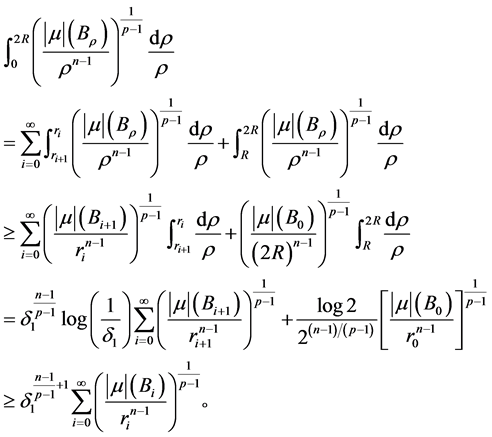 (2.18)
(2.18)
所以,由(2.12)式和(2.13)式的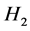 ,可知
,可知
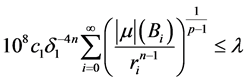 , (2.19)
, (2.19)
且
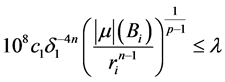 。 (2.20)
。 (2.20)
第二步. 由(2.17)式,不失一般性,我们可假设存在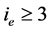 ,使得
,使得
 且
且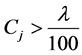 ,
,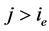 。 (2.21)
。 (2.21)
否则,对递增序列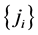 (任意
(任意 ),都有
),都有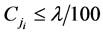 。由于
。由于 是
是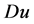 的一个Lebesgue点,则有
的一个Lebesgue点,则有
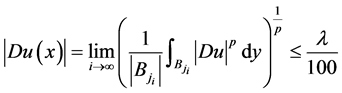 。
。
故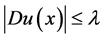 ,结论得证。
,结论得证。
第三步. 下面我们在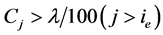 情况下继续定理1.1的证明。简记
情况下继续定理1.1的证明。简记
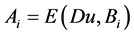 且
且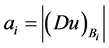 。
。
由(2.15)式和(2.21)式,可知
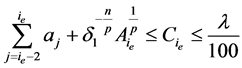 。 (2.22)
。 (2.22)
现在,我们用归纳法证明:当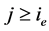 时,有下式成立
时,有下式成立
 。 (2.23)
。 (2.23)
即假设当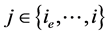 时,(2.23)式成立,证明
时,(2.23)式成立,证明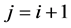 时,(2.23)式仍成立。首先,由引理2.3可知
时,(2.23)式仍成立。首先,由引理2.3可知
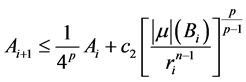 ,
,
即
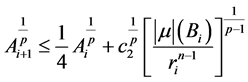 。 (2.24)
。 (2.24)
结合(2.20)式和(2.23)式,有
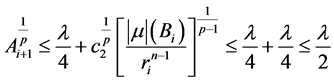 。 (2.25)
。 (2.25)
进一步,由(2.24)式对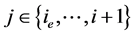 求和,可得
求和,可得
 ,
,
因此
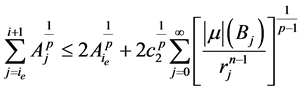 。 (2.26)
。 (2.26)
另一方面,又因为
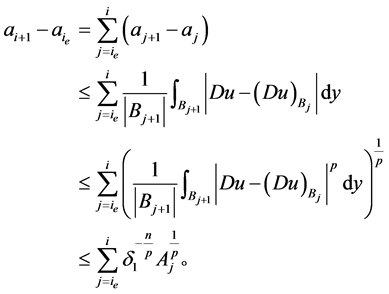
结合(2.19)式,(2.22)式和(2.26)式,可得
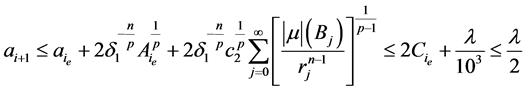 。
。
所以,由(2.25)式和上式,即有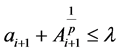 成立。综上所述,对任意
成立。综上所述,对任意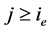 ,(2.23)式成立。最后,由于
,(2.23)式成立。最后,由于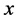 是
是 的Lebesgue点,故
的Lebesgue点,故
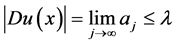 。
。
从而我们完成了定理1.1的证明。