1. 引言
银行的资金来源主要是高流动性的存款，在总资金来源中占了2/3以上。银行业务扩展的基础是有充分的存款，如果存款吸收较少或不吸收，单纯靠银行极其有限的资金作为营运资金，则银行业务得不到扩展，银行无法生存。银行的盈利方式主要分为利差收入和非利差收入，利差收入是贷款利息收入与存款利息支出的差额，它是以存款为基础的，只有吸收更多的存款，银行才能扩大贷款规模，获取更多利差收入。如果失去了这个基础，银行的盈利不仅缺失很大比重，开展银行资产业务、中间业务也不存在了，零售业务利润和转型更无从谈起。定期存款具有稳定性强、成本低的特点，对中、长期贷款功不可没，所以存款对银行非常重要。
定期存款是银行和存款人事先约定存款期限的存款，它是银行稳定的资金来源。银行定期存款主要是由居民个人资产构成，具有单笔金额低、客户群体大的特点，只有积聚了相当数量的客户群体，银行才能从中甄别目标客户，将个人银行服务从单纯的存、取款服务向储蓄、个人贷款、代理理财并重的多元化服务方向转变，从这个角度讲，定期存款背后的客户群体为银行不断创新金融产品提供了广阔基础，为发展个人消费信贷、财富管理、信用卡等中间性收费业务，实现利息收入和手续费收入提供了源泉。现阶段，在未完全实现业务转型的前提下，存款规模小就意味着客户基础薄弱，会直接影响零售业务的发展，进而影响业务经营转型的进程，降低银行整体竞争力 [1] 。
如今是多媒体时代，电视、报纸、广告等都只是把消息传递给消费者，而电话可以和消费者进行沟通。电话营销自问世以来，以其成本低、效率高、覆盖广的优势，正在被越来越多的现代企业所采用。它可以反馈消费者信息，更加高效地维护和扩大消费者范围，密切企业和消费者的关系，增强客户对企业的忠诚度，最终以较低的成本付出获取较高的利润回报。目前，各银行电话销售业务已初具规模，但由于系统字段记录不充分，数据挖掘和分析技术不完善，目前的电话营销仍处在“大量定制”自动外呼阶段，电话营销的成功率并不是很高 [2] 。
因此基于现有信息银行如何提高电话营销率获得更多定期存款是个急待解决的问题。
我们知道，支持向量机方法可以处理不确定性和非线性的关系的变量，所以可以对是否订购定期存款进行预测。但是影响订购定期存款的因素很多，各个影响因素之间可能会存在多重共线性，如果不加选择地引入众多影响因素来进行定期存款的预测，往往不能取得良好的预测效果。一个理想的模型应该是既不遗漏重要的自变量，也不包含没有影响或影响很小的自变量，过多地引入变量不仅会大大增加计算量，也会降低估计和预测精度 [3] 。
虽然支持向量机方法比较适合处理具有非线性关系的小样本数据，但是不能进行变量选择，而LASSO (The Least Absolute Shrinkage and Selection Operator)方法可以同时进行参数估计和变量选择，LASSO方法可以处理分类数据，所以，本文提出了基于LASSO与支持向量机的订购定期存款组合预测方法。首先利用LASSO方法对定期存款的影响因素进行选择，剔除与定期存款不相关或相关性很小的变量数据，以达到降低数据维数的目的；然后利用支持向量机的非线性运算能力，逼近历史数据所隐含的函数关系，完成对定期存款的拟合和预测 [4] 。同时，比较支持向量机、LASSO与支持向量机结合的方法、神经网络、LASSO与神经网络结合的方法这四种方法的拟合预测效果。
2. 模型介绍
2.1. LASSO方法
LASSO算法是Tibshirani (1996)提出的一种降维方法，本质是通过惩罚函数将对因变量没有影响或影响较小的自变量的回归系数压缩到0，可以有效消除多重共线性的影响。
为了消除指标量纲的影响，在使用LASSO方法时，需要对数据进行标准化处理，即满足：
，
，其中
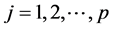。LASSO估计定义公式：
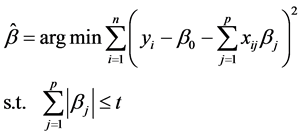(1)
t是调和参数，当t充分小时将导致某些系数恰好为0，这样就是实现了变量选择 [5] 。
2.2. 支持向量机方法
在机器学习领域，支持向量机(Support Vector Machine, SVM)是一个有监督的统计机器学习模型，通常用来进行模式识别、回归、以及分类分析，SVM一般用在二分类的问题上。模型的基本定义就是能够有一个线性分类器，比如最简单的 [6] ，一个平面上的两类不同的点，如何将它用一条直线分开？在平面上我们可能无法实现，但是如果通过某种映射，将这些点映射到其它空间(比如说球面上等)，我们有可能在另外一个空间中很容易找到这样一条所谓的“分隔线”，将这些点分开。SVM的做法是 [6] ：将所有待分类的点映射到“高维空间”，然后在高维空间中找到一个能将这些点分开的“超平面”，也就是通过一个非线性映射p，把样本空间映射到一个高维乃至无穷维的特征空间中(Hilbert空间)，使得在原来的样本空间中非线性可分的问题转化为在特征空间中的线性可分的问题 [7] 。当三维线性不可分时，现在我们将其旋转映射到某个高维空间得到平面可分情况。然而“超平面”不是唯一的，支持向量机需要的是利用这些超平面，找到使得这两类点之间的最大的那个超平面。此时，我们利用平面二分类来说明，此时我们有无数多条线可以完成这个任务，因此我们需要寻找一条最优的分界线使得它到两边的margin都最大，在这种情况下边缘加粗的几个数据点就叫做support vector，这也是这个分类算法名字的来源 [8] 。
上文提到的低维空间到高维空间的映射也就是核函数，SVM就是通过选择核函数来解决在原始空间中线性不可分的问题，常用的核函数有以下4种：
1) 线性核函数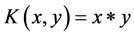
；
2) 多项式核函数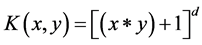
；
3) 径向基函数
；
4) 二层神经网络核函数
。
支持向量机是一个针对二分类的分类凸优化问题，同时也是个二次规划问题，我们使用拉格朗日乘子来描述一个二次规划解(包括目标函数和约束条件)，可如下等价表述为：
(2)
再加入松弛变量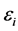
后，意味着我们放弃了对某些点的精确分类，而这对我们的分类器来说是种损失。但是放弃这些点也带来了好处，那就是使分类面不必向这些点的方向移动，因而可以得到更大的几何间隔(在低维空间看来，分类边界也更平滑)。显然我们必须权衡这种损失和好处，希望损失(cost)越小越好，因而损失就必然是一个能使目标函数变大的量。这里把损失加入到目标函数里，就需要一个惩罚因子
，原来的优化问题就变成了下面这样：
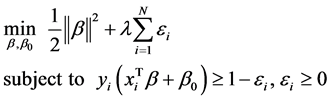(3)
SVM最终将这个二分类过程转化为一个二次规划的优化求解的过程。
2.3. LASSO-支持向量机方法
首先用LASSO变量系数最小绝对值压缩的方法去除对因变量影响较小的自变量，获得低维度数据；然后用交叉验证算法结合LASSO特征选择方法获得的变量构建SVM模型，然后用构建好的模型对测试样本进行分类预测。
3. 实证分析
3.1. 数据简介
本文采用的数据是来自UCI网站中葡萄牙银行机构的电话定期存款营销活动数据，研究目的是对客户是否订购银行定期存款做一个预测，因此响应变量是一个二分类变量，订购记为1，未订购记为0。并且本文使用15个变量作为解释变量，共有4521个样本量。各解释变量取值范围及含义如表1。
3.2. 分析数据
3.2.1. 描述性统计
为了对数据有整体性认识，我们对本文数据进行简单描述性统计分析如下，Y是响应变量，即：客户是否订购银行定期存款。
表2中的数据比重代表所对应的样本量占订购定期存款总样本量或不订购定期存款总样本量的比重，如：job目前在工作所对应的比重82.15%，指订购定期存款的样本数占总订购定期存款的样本数的比重；job目前在工作所对应的比重90.325%，指不订购定期存款的样本数占总不订购定期存款的样本数的比重。
表1. 变量介绍
Table 2. Classification data sample size and proportion
表2. 分类型数据样本量及比重
从表2的简单描述性数据可以看出， 订购成功所对应的变量占得比重明显大于不订购成功所对应的变量占得比重的有education、contact、loan、poutcome这几个变量，说明这几个变量对订购成功与否产生较大的影响，这几个变量所代表的含义：大学、移动电话联系、无个人贷款、上次项目成功对于订购成功产生促进作用，也符合实际情况。对于其它的变量，订购成功所对应的变量占得比重与不订购成功所对应的变量占得比重差别不大，说明这些变量对订购成功预付影响较小或者由于数据的原因没有表现出来。
从表3可以看出，对于联系时间(duration)，订购定期存款的联系时间均值要远大于不订购定期存款的联系时间均值，说明联系时间的长短反映了订购成功与否，如果订购联系时间就要久一些，这符合实际情况。因为如果要订购就会了解的详细一些，相应的联系时间就会久一些。对于该项目中联系总次数(campaign)，订购与否并没有大的差别，想反不订购的联系总次数均值还大于订购总次数的均值，说明联系总次数对订购与否没有影响。对于最近一次联系距今日期(pdays)来看，订购定期存款的联系日期要远大于不订购定期存款的日期，因为未联系过的日期记为-1，而不订购定期存款的样本量占了8/9，未联系过的样本量有3368个，这在一定程度上拉低了均值，所以由于数据的原因这个变量的均值比较没有实际意义。对于该次项目之前的联系总次数(previous)，订购定期存款的均值要大于不订购定期存款的均值，说明之前联系次数对订购成功与否会有影响，联系的越多订购成功的可能性越大。年均余额(balance)对于两者的影响没有太大的差别，说明对订购成功与否差别不大。
3.2.2. SVM模型分析
本文共有4521个样本量，其中成功订购的样本量有521个，未成功订购的样本量有4000个，从这可以看出电话营销成功率不高。因为成功订购与未成功订购银行定期存款的样本量差距过大，会对预测产生较大的偏差影响，所以在进行数据分析时首先要平衡数据。本文采用随机抽样的原则，从未成功订购银行定期存款的样本量中抽取与成功订购样本量相同的数量，即521个样本，然后与成功订购银行定期存款的样本量构成一个新的数据集。本文针对新数据集进行预测和分析。
分析数据可以看出，数据需要判别的是两个类别，且两个类别属于字符类型，所以我们可以选择的支持向量分类基就有三类：C-classification、nu-classification、one-classification。同时，可以选择的核函数有四类：线性核函数(linear)、多项式核函数(polynomial)、径向基核函数(radial basis, RBF)和神经网络核函数(sigmoid)。所以应该尽可能建立所有可能的模型，最后通过比较选出判别结果最优的模型 [9] 。根据上述分析，利用R实现的预测模型就有12个，每个模型都对应一个预测精度，我们可以看到每个模型预测错误的总个数。我们可以根据这个预测结果挑选出预测错误最少的一些模型，然后再根据实际情况进行详细分析，最终决定出适合本次研究目的的模型。
从表4中的模型预测结果可以看出，利用one-classification方式无论采取何种核函数得出的结果错误
Table 3. Mean value of numerical data
表3. 数值型数据均值
都非常多，所以可以看出该方式不适合这类数据类型的判别。使用one-classification方式进行建模时，数据通常情况下为一个类别的特征，建立的模型主要用于判别其它样本是否属于这类。
继续观察其它两种分类方式，可以发现利用nu-classification方式无论采取何种核函数得出的结果错误都相对较少，所以可以看出该方式比较适合这类数据类型的判别。利用nu-classification与径向基核函数结合的模型判别错误最少，我们可以直接选择这个模型作为最优模型。利用该模型作出的预测结果如表5所示。
由表5预测结果可以看出，在1042个样本中，实际属于不订购(no)的有521个，而由判定结果可以看出，521个样本有454个判定正确，67个错判为订购(yes)。两个类别分别有454、429个样本被正确分类，其中不订购被正确分类的样本较多。且正确分类的样本量为883个，正确率则可以通过计算得到，883/1042 = 0.8474。精确度为429/(429 + 67) = 0.8649，召回率为429/(429 + 92) = 0.8234。
3.2.3. LASSO-SVM模型分析
在运用LASSO方法变量选择时，首先把数据进行标准化处理，以消除不同指标量纲的影响。利用R软件中的Glmnet程序包，通过10折交叉验证选出的惩罚参数lambda = 0.009163099进行变量选择，表6为选出的变量系数。其中age (年龄)、job (是否工作)、marital (婚姻状况)、education (教育水平)、balance (年均余额)、housing (是否有房贷)、loan (是否有个人贷款)、 contact (联系方式)、day (最近一次联系的日期)、duration (最近一次联系的持续时间)、campaign (该项目中联系总次数)、pdays (最近一次联系距今的日数)、poutcome1 (之前营销项目的结果——“成功”哑变量)、poutcome2 (之前营销项目的结果——“失败”哑变量)，这些经过筛选出来的变量在某种程度上来说对于订购定期存款的影响是比较大的。
变量poutcome1的系数最大，说明之前营销项目的结果对这次订购定期存款的结果影响较大；job的系数为负，说明目前不在工作的更易订购定期存款，因为目前不在工作的有很多都是退休职工，他们定
Table 4. Corresponding prediction results
表4. 相应的预测结果
Table 5. 0ptimal model prediction results
表5. 最优模型预测结果
表6. 模型系数
期存款是为了保障自己的晚年生活；housing的系数为负，说明没有房贷的更易定期存款；day的系数为负，说明每个月的下半月更易定期存款，因为很多公司都是中旬发工资，下半月刚好工资到账，所以很多人选择下半月定期存款。
根据LASSO选出的变量进行SVM建模，核函数的选择会影响着支持向量机的分类好坏，我们选择前文提到的四种常见的核函数和3种支持向量分类基构建12个分类模型，每个模型的预测错误总样本数如表7。
从表7可以看出，经过LASSO变量选择后，模型预测错误样本数有所下降，说明经过LASSO变量选择后模型预测准确率提高。从表中的模型预测结果可以看出，利用one-classification方式无论采取何种核函数得出的结果错误都非常多，这和没有经过变量选择预测结果一样。
继续观察其它两种分类方式，可以发现利用nu-classification与多项式核函数结合的模型判别错误最少，我们可以直接选择这个模型作为最优模型。利用该模型作出的预测结果如表8所示。
经过变量选择后不订购定期存款的预测准确样本量增加较多，订购定期存款的样本量预测正确的只增加一个，说明选择出来的变量对不订购定期存款的影响较大。两个类别分别有434、473个样本被正确分类，其中不订购被正确分类的样本较多。且正确分类的样本量为907个，正确率则可以通过计算得到，907/1042 = 0.8704。精确度为434/(434 + 48) = 0.9004，召回率为434/(434 + 87) = 0.8330。
3.3. 结果分析
为了更清晰的看出LASSO变量选择效果，本文还构建了神经网络(Neural Networks，简写为NN)和LASSO-NN模型。通过对不同模型的预测效果比较，以期更全面考察LASSO-svm方法的实际效果。预测模型预测效果一般通过对样本预测准确率表示，并用两类准确率来度量：第一类准确率为将实际订购定期存款的预测正确；第二类准确率为将实际不订购定期存款的预测正确。这四种模型的预测结果具体如表9所示。
从表9可以看出，无论是SVM还是NN模型，经过LASSO变量选择处理后的预测效果都要好于处理前的预测效果。具体来说，LASSO-SVM模型的效果最好，不管是总预测准确率还是第一类准确或第二类准确率都是最高的，其第一类准确率为83.30%，第二类准确率达到90.79%，总预测准确率为87.04%。其次是SVM模型，其第一类和第二类准确率分别为82.34%、87.14%，总预测准确率为84.74%。而另外两种模型的准确率，其第一类准确率分别为78.69%、82.92%，第二类准确率分别为82.73%、82.92%，这两种模型的总预测准确率也分别为80.71%、83.88%，都低于前两种模型的预测准确率。
Table 7. Corresponding prediction results
表7. 相应的预测结果
Table 8. Optimal model prediction results
表8. 最优模型预测结果
Table 9. The results of prediction of four models
表9. 四种模型的预测结果
说明经过LASSO变量选择后，模型的预测准确率提高了。但是无论是神经网络还是经过变量选择后的神经网络预测效果都要低于SVM的预测效果。
4. 结论
在对某一种情况进行预测时，需要引入很多的变量来刻画它，但是不加选择的引入过多变量来进行预测，往往不能取得良好的效果。这是因为过多地引入复杂性变量会导致“维数灾难”和“组合爆炸”，使得计算量空前增大，估计和预测精度也会下降；此外，在一些情况下，获得某些变量的数据代价昂贵，如果这些数据本身对预测结果的影响微乎其微，那么势必会造成缺陷数据的收集和模型应用的费用不必要地增大。针对上述问题，混合统计与机器学习方法的核心是先利用统计方法的思想对要进行预测的数据集进行特征选择处理，达到降低数据集维数的目的；之后用机器学习方法对处理后的数据集进行预测，获得所需要的预测精度。本文基于上述思想，提出了一种基于LASSO-SVM 的预测方法。并与SVM、 LASSO-SVM及神经网络、LASSO-神经网络方法的拟合预测效果进行比较，验证了该方法的有效性和预测准确率较高的特点 [10] 。本研究的主要结论有：
第一，根据本文所用数据可知，订购定期存款的样本量大约占总样本量的8/9，说明银行电话营销订购定期存款的准确率不高。
第二，从描述性统计分析结果来看订购成功所对应的变量占得比重明显大于不订购成功所对应的变量占得比重的有education、contact、loan、poutcome这几个变量，说明这几个变量对订购成功与否产生较大的影响，这几个变量所代表的含义：大学、移动电话联系、无个人贷款、上次项目成功对于订购成功产生促进作用，也符合实际情况。银行在进行电话营销时可以多从这几方面考虑，针对高学历、无个人贷款、上次营销产品成功的人进行移动电话联系推荐。
第三，无论是经过变量选择还是不经过变量选择的模型，对定期存款都有一定的预测能力。但从具体模型结果来看，原始数据经过LASSO变量选择后的预测模型其效果要好于不经过变量选择的模型预测效果，这也验证了经过变量选择，能极大降低模型的输入维数达到简化模型结构，从而提高模型的预测效果。
第四，无论在不在相同的LASSO变量选择下，神经网络方法预测的准确率总体来看要低于SVM模型的预测准确率，说明SVM模型更适合预测该数据。因为该数据变量有很多是分类数据，SVM更适合处理非线性的小样本数据，所以它的预测效果比神经网络模型的预测效果好。