1. 引言
热量传递方式有导热、对流与辐射。由于导热和辐射传热的强化受到限制，所以对流换热的强化研究受到很大重视。对流换热现象广泛存在于自然界和各种工程问题中 [1] ，在动力、核能、石油化工、航空航天等领域中的应用尤其受到关注。Rayleigh-Benard (BR)热对流系统是从众多自然现象中抽象出来研究对流问题的经典流体力学模型，对于RB系统的研究开始于上世纪初，1990年Benard首次实验研究了热浮力驱动流体流动的现象 [2] 。1916年Rayleigh以Navier-Stokes方程为基础建立了热浮力驱动流体对流流动的运动方程 [3] ，此后100年间RB研究得到迅速的发展。例如：在流动稳定性理论的发展中RB系统起到了至关重要的作用 [4] [5] ；上世纪80年代末的“芝加哥对流实验”是现代RB系统研究的一个重要里程碑 [6] [7] [8] ，该实验表明在Ra数逐渐增大时RB系统内的流体流动将先后进入“软湍流”和“硬湍流”两个重要的湍流状态区间。随后，RB系统的研究重心由对系统流动稳定性和混沌模式形成的研究转入对湍流状态下系统各物理量统计特性的研究 [9] 。
美国Bergles教授对强化对流换热文献进行了年度统计，研究发现从1861年焦耳发表的第一篇冷凝器水侧强化换热的报告到上世纪50年代，关于强化对流换热的文章并不多，而从上世纪中期开始，对流换热的研究却逐渐成为传热学的重要研究方向 [10] [11] [12] [13] [14] 。按照Bergles的分类，换热强化方法可以分为有源技术(active technology)和无源技术(passive technology)两种。所谓有源，即须依赖外界机械力、热源或电磁力；而无源，则是除了输送传热介质的功率消耗外，不再需要其他附加动力。目前应用比较广泛的属于有源强化技术的有加入扰动流体法、垂直旋转轴法、脉冲法等；而无源强化方法有粗糙表面法、热对流分区法、横向限制湍流法等。本文将系统评述上述各种增强RB对流强化换热技术的方法，并对其特征及优缺点作评述。
2. 有源技术
2.1. 多相RB对流换热系统
多相流动体系指的是由两种或一种连续介质和若干种离散介质组成的连续性体系。连续介质称为连续相，离散介质(如固体颗粒、水泡、液滴等)称为分散相(或非连续相)。多相物体的流动现象广泛存在于自然界、日常生活及工程实际中。一般可认为，绝大多数的流动都是多相流，纯粹的单相流(如极纯净的气体或水等)是极为少见的。多相流体系中最为常见的是两相流系统，它是关于分散相在连续相中的运动规律及其反应过程的影响。在RB对流中，分散相为液滴或气泡时，有很多特点。例如，液滴和气泡在运动中会变形，在液滴或气泡内出现环流，界面上有波动，表面张力梯度会造成复杂的表面运动等 [15] [16] 。现主要分析汽液两相流对对流传热的影响。
研究发现，从底部加热的以乙烷(C2H6)为样品的湍流热传输装置，当使其上下表面温差跨越样品气液共存曲线时，汽化潜热H会提供一个附加的导热传输机制，导致有效导热系数
随着Tt的降低呈现线性增加趋势，并最终到达一个最大的导热系数
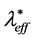，其值比单向作用下的导热系数
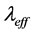大了约一个数量级。特别是压力P接近临界压力时，即使在汽化潜热H消失的情况下，最大导热系数
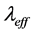也会急剧增加。Jin-Qiang Zhong [17] 认为这种现象是由于在接近临界点附近液滴的成核率得到一个有效的增强导致。L.Biferale等人 [18] 通过一种高分辨率数值模拟多相流动的对流(沸腾)算法模拟了该实验过程。
2.1.1. 实验装置及步骤
为研究这一现象，实验 [17] 采用一种圆柱体样本，其直径D等于高度L，以乙烷(C2H6)作为实验气体，测量其在略低于临界点(CP)时的导热系数
，同时样本压力P及上下板温差
均保持恒定，考虑到在上板会出现一个较大的热量梯度，实验还应关注当Tt逐渐从略高于Tø减少至低于Tø时热量传输
的参数范围。该装置已多次被用于湍流贝纳特流的测量。通过阴影法图像显示，发现此时液滴的凝结主要珠状凝结而不是膜状凝结，当临界压力时，汽化潜热H消失，但最大导热系数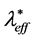
会急剧增加。
2.1.2. 实验结果分析
由于热量传播不仅取决于汽化潜热，还依靠成核速率，实验表明当系统处于临界压力时，整个流体处于气液共存状态，此时的汽化潜热减小，但系统整体传热却反而得到增强，此时起决定作用的是成核速率，由此可得出结论，成核速率在临界压力附近对热量传播的影响较之汽化潜热更大，之后的实验考虑了顶板表面粗糙度对成核速率的影响，结果也显示表面粗糙度对于成核速率的影响并不十分明显，且成核过程在整个板平面是均匀发展的。
2.1.3. 结论
在湍流RB中，当应用温差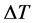
跨越气液共存曲线，会导致有效导热率线性增加，甚至比单相对流中导热率大一个数量级或更多，与此同时，当压力P接近于临界压力时，会导致一个最大换热量PCP。由于在临界点处汽化潜热H消失，但液滴成核率的增长克服汽化潜热消失带来的影响，导致导热率仍然上升。
目前更深入的研究有在两相流中加入纳米流体可使得RB流得到进一步强化，或是将两相流的强化作用推广到三相流中，这些有待之后的实验跟模拟来检测。
2.2. 通过旋转增强换热
旋转湍流对流动力学的影响是由相关的全球规模的科里奥利力(科氏力)和浮力的比值所决定的 [19] - [24] ，旋转效应不仅改变流体的平均运动，同时也改变湍流的强度和脉动结构。Pallares和Davidson [25] [26] 采用大涡模拟的方法对此进行了数值模拟研究。Eric M. King [27] 等人认为该转换是通过热(非旋转)和埃克曼(旋转)边界层的相对厚度来控制，并在两种边界层竞争的基础上制定了两个区域过渡的描述。
如图1(a)，快速旋转流通常由转动轴产生的科氏力引入到细长的连贯对流列中。这种形式的影响，是由地球内部磁场的强度结构决定。当热流压迫增加，使得相对旋转的影响减弱，从而图1(b)的三维湍流对流产生。目前普遍支持的观点就是当全球规模浮力与科氏力的比值小于其统一状态下时，旋转将成为影响对流的主要形式。此结论可通过耦合实验和数值实验的方式得出，控制对流的主要形式是边界层
(a) (b)
Figure 1. Numerical experiments of the vertical velocity Iso- surfaces diagram. (a) E = 10−4, Ra = 5 × 106, Pr = 7. A large scale, coherent, axial typical rotational velocity convection dominated alignment structure is presented. (b) E = 10−4, Ra = 2.1 × 108, Pr = 7. Display a typical non rotating three-dimensional con- vection structure [27]
图1. 数值实验的垂直速度Iso-surfaces图。(a) E = 10−4，Ra = 5 × 106，Pr = 7。呈现的是一种大尺度、连贯、轴向的典型旋转速度对流主导的对齐结构。(b) E = 10−4，Ra = 2.1 × 108，Pr = 7。显示的是一种典型的非旋转三维对流结构 [27]
动态而不是全球规模力平衡 [27] 。
先前许多的研究证明了旋转对流系统的存在，但对于旋转对流换热没有统一的描述，通常情况下，我们以Nu和Ra数作为传热效率的标度律。Nu = 1为纯粹的热传导，更高的Nu表明了更高效的对流换热。在对流换热中，
许多非旋转对流实验以
为标度尺度，而旋转对流实验一般以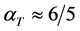
作为标度尺度，不同标度尺寸的选择也引起了天体物理或地球物理参数领域产生多个数量级的预测。
根据边界层动力学，对流流体区域包含两种截然不同的动态区域：内部流体以及边界层。在非旋转的湍流区域，扩散的影响可以忽略不计，唯一限制传热的就是热边界层的产生，同时对流量的增加可导致热边界层厚度变薄。而在旋转流体力学中，旋转的强度是以粘性力与科氏力的比值为特征，即埃克曼数：
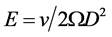
其中埃克曼边界层厚度
，因此埃克曼边界层随着旋转速率提高而变薄。
2.2.1. 实验步骤
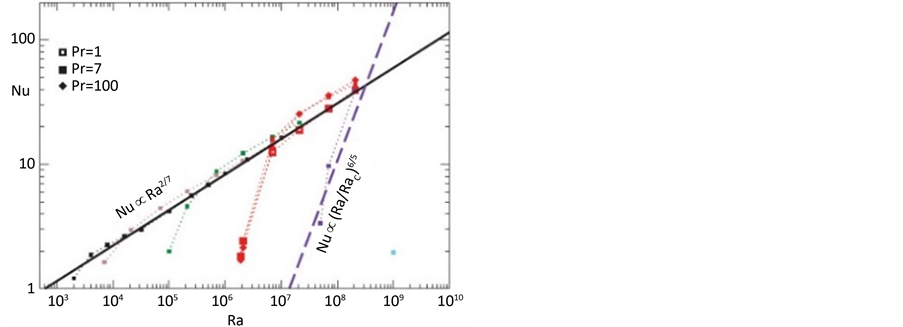
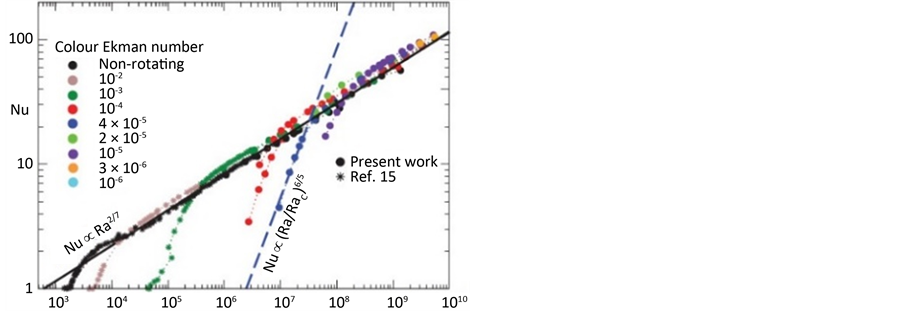
在旋转对流实验中，可通过改变加热速率来改变热边界层厚度，改变旋转速率改变埃克曼边界层厚度。几种不同的流体以Pr数作为对比参数，Pr = v/k。不同的普朗特数流体产生稍有不同的非旋转缩放因子，但其影响较弱，当考虑到旋转时，由于科氏力的稳定效果使得对流的产生延迟了，一旦对流产生，传热显示出更陡峭的特性，如图2 [27] 。
这与先前认为的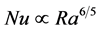
相符合，因此，可以验证旋转控制机制中Nu正比于Ra6/5的结果。继续比较过渡瑞利数Rat和努尔数Nut，发现当Ra < Rat，受旋转影响的对流的传热效率不及非旋转的对流；当Ra > Rat，传热受旋转影响并不明显。其结果支持边界层转换的假设。
进一步在E = 10−4和Pr = 7的数值实验条件下测量边界层厚度。当热边界层厚度大于埃克曼层，对
(a) (b)
Figure 2. Nu number and Ra number log map. (a) Experimental data obtained, (b) Numerical simulation data
图2. Nu数与Ra数对数图；(a) 实验取得数据，(b) 数值模拟数据
流表现为湍流；相反，当埃克曼层比所述热边界层更薄，旋转的影响控制对流以及限制流体运动。对于边界层控制转换比例Ra/Rat，广泛适用于自然对流系统，由于Ra很难在自然下直接观测，而通量瑞利数
，取决于整体浮力通量，对于热对流：
Rat和Nut构成了一个过渡性的通量瑞利数，其值Raf，t = 0.25E−9/4。
2.2.2. 结论
综合流体性质，系统尺寸，和旋转速度及热通量，可确定一个完整的对流机制，并借此可求得地壳层的瑞利数Ra ≈ 7 × 1024，表明核心对流只是发生在边界层过渡以下，并使转变作为核心动力。
实验和数值模拟表明，在RB流中，适当的旋转导致相对适中的Ra ≈ 108和Pr数，可提高换热达30%，但当Ra过大时，热量传输效率会降低。甚至当Pr ≤ 0.7，热量增强会彻底消失。之后的研究方向主要是优化旋转速率等可变因素，使得其换热效果达到最佳。
2.3. 脉冲法
在RBC中投入周期的脉冲能量，当脉冲以正弦或常量的形式投入，RBC的传热效率都得到有效的增强，Nu平均增加了7%。研究发现，增强换热取决于两个方面：一是驱动能量的投入是否与湍流时间尺度同步，当投入能量的周期等于大规模流动周期时间的一半时，能够得到一种共振的强化；二是取决于脉冲的波形(形式)，由实验可知，尖脉冲比平脉冲更能有效增加热量传输。因此，XIAO-LI JIN [28] 等作出假设，存在适当范围内的驱动力A以及驱动频率f可使得瑞利数在低饱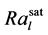和值
和高饱和值
之间达到一个合适的饱和值Ra。根据A跟f的幂律法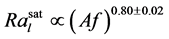
以及
，
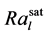标度律也与之前预测的驱动湍流平均场理论想吻合 [29] 。
目前的研究提供了一个范例，通过制动控制排放聚集热羽流第一次触发的时间，然后同步羽流群内部的运输时间尺度，可以实现强化换热系统。一种方法是通过周期脉冲作为能量输入的手段驱动湍流 [29] ，可以发现由于驱动力以及驱动频率的影响使得Ra数增长并达到一个饱和值，在Hooghoudt [30] 等人的数值分析中得到类似结果。另一种方法是通过正弦调制的能量输入外长度尺度湍流系统，Heydt利用平均场理论，研究了湍流系统对弱调制能量输入的响应，并预测其与调制频率和能量串联频率等有关。对于低频驱动，系统几乎遵循恒幅调制，然而在高频条件下，反向调制频率大大降低。后续的数值模拟也直接或间接验证了这些理论 [31] [32]
2.3.1. 实验介绍
为研究定期驱动湍流在RB腔中的影响，已知流体被三个控制参数限制：Ra、Pr以及装置纵横比 。实验采用两个充满水的立式圆筒形室，直径D均为19.4 cm，高度H分别为19.4 cm和39.2 cm。上下板材料为铜，四周是透明有机玻璃管，下板由程控电源控制，使脉冲加热得以系统实施。上板由一个冷藏再循环装置控制，使保持恒定温度。整个对流室由几层绝缘材料包裹，并置于恒温箱中(平均温度40℃)，恒温箱有一个0.05℃的温度稳定性。用于实时监控温度的5个2.4 mm直径的热敏电阻，被安装在上下板。t = 0时，对下板进行脉冲加热。Ra数和Nu数由三种脉冲参数脉宽
，脉冲间隔时间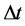
以及脉冲振幅P决定。
2.3.2. 实验结论
如图3实验数据表明，对于Ra数，每个脉冲周期都会出现一个峰值以及随后的衰减，当脉冲频率f足够大时，Ra数达到一个饱和值Rasar，并且在f增加，饱和Ra数也随之增加，但峰值和谷值Ra的差距却减小，比较不同频率和不同的驱动力A下Rasat值，可发现当其大于一特定值时，整个对流可视为在湍流状态；总结两个圆筒室的结果，得出下列两组关系：
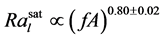
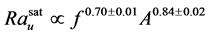
进一步分析下板、上板、室中央以及侧壁温度波动的标准差，可分析得出热羽流主要发生在侧壁区 [33] 。对于Nu，实验表明，当脉冲周期Tkick在一个合适的范围内时，Nu数得到有效的增强，且当Tkick ≈ Tlsc/2时，整个系统达到共振，增强效果得到最优化，因此脉冲加热比传统的热量传播更有效率。而特定波形对Nu数的增强作用，主要通过两个因素的影响：脉冲周期与湍流固有时间尺度的同步性以及波形的影响。
因此，综合Lohse的平均场理论 [29] ，饱和Ra数是介于低饱和水平和高饱和水平之间波动的，而其饱和水平的尺度，取决于驱动力A和驱动频率f，脉冲引起的大尺度环流(LSC)仍存在于RBC系统中 [34] ，
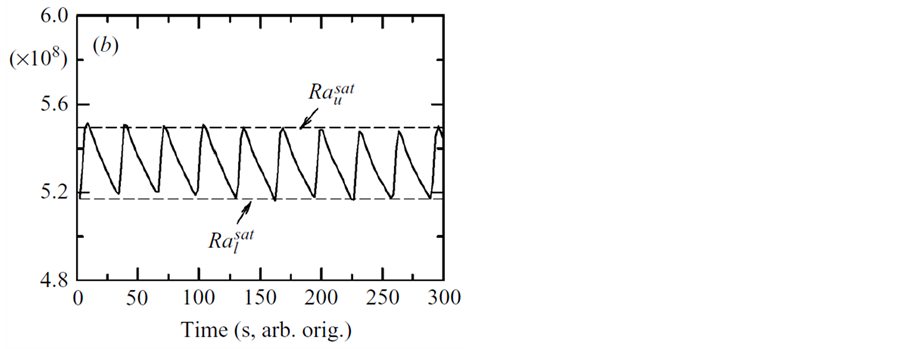
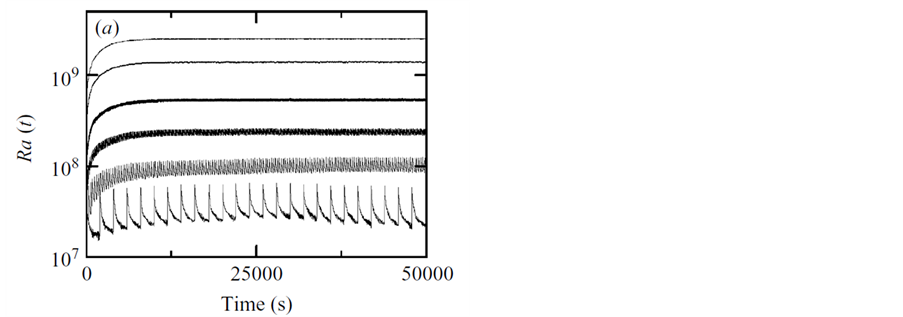
Figure 3. Ra number and time function at different frequencies. (a) In the aspect ratio of 1, in which the driving force A = 347.66 J, the driving frequency is 5 × 10−4 Hz，3.36 × 10−3 Hz，1.13 × 10−2 Hz，3.33 × 10−2 Hz，1.25 × 10−1 Hz和3.33 × 10−1 Hz. (b) The time-varying image of a saturated Ra(t) is measured under the driving force A = 347.66 J and f = 0.033 Hz [28]
图3. 不同频率下Ra数与时间函数图(a)在纵横比 为1的室中，其中驱动力A = 347.66 J，驱动频率至下而上，大小分别为5 × 10−4 Hz，3.36 × 10−3 Hz，1.13 × 10−2 Hz，3.33 × 10−2 Hz，1.25 × 10−1 Hz和3.33 × 10−1 Hz. (b) 测量的是一段饱和Ra(t)在驱动力A = 347.66 J以及f = 0.033 HZ下随时间变化图像 [28]
其强度与稳定驱动下的湍流系统一致，所以脉冲对Nu的加强，是与合适脉冲参数的选择有关，接下来的工作就是对于驱动湍流进行初步的实验研究，例如长周期的驱动能力投入对自衰湍流热对流系统的间歇影响，以及在驱动频率远大于LSC周期的情况下大尺度环流是否仍然存在。
3. 无源技术
3.1. 粗糙表面对换热的影响
粗糙表面上的湍流流动是自然界中普遍存在的，一个明显的例子就是大气和海洋中的流体对流现象，其底层表面几乎是粗糙的。研究湍流在粗糙表面的换热主要是研究边界层的结构与动力学的关系，目前关于粗糙的对湍流流动的影响很大程度来自于风洞试验和其他开放系统 [35] 。由于在壁面附近扰动产生的扰动流是封闭的，并迅速向下游排放，因此表面粗糙通常没有过多的扰动大部分区域，其效果往往可通过调整表面粗糙度值K等相关参数来调整 [36] 。这种情况完全改变一个封闭空间内的流体，其中所产生的边界扰动是不可避免的混合成湍流的块状区域。
目前湍流Rayleigh-Benard对流作为封闭系统的一个特殊案例，近年来逐步引起人们的关注。研究发现，在一个粗糙的上下表面封闭的空间中进行对流实验，当控制热边界层厚度在一定范围内时，整个粗糙空间的热传导增加76%以上，从热边界层间歇爆发的热羽流和相干大循环，通过剪切边界层，被发现在对流空间共存。这些特点与空间上的热量传输直接相关，并通过几种理论模型 [37] [38] [39] 观察到。YAN [40] 将粗糙表面与射流冲击相结合的复合强化传热技术以及Zhang [41] 将粗糙表面引申至微细通道内流动，均取得很大的进展。
3.1.1. 实验介绍
实验在一个充满水的圆柱体空间内进行，圆柱的上下面均由相同的带有V型槽的黄铜片构成。凹槽顶角为90˚，每个V型槽的高度K为9.0 mm，间接是2 k。圆柱体壁面是由有机玻璃构成的，两个圆柱环具有相同的内径20 cm，高度分别为20和40 cm，对应的纵横比为1和0.5。上板通过安装在板顶部的冷却腔进行冷却，下板是在板的背面电热膜进行均匀加热。两板间的温差△T由嵌入板内的热敏电阻测量，对流流体中心轴附近局部温度由一个小的可移动温度探头测量。实验中控制的参数是瑞利数
3.1.2. 结果分析
图4 [42] 中显示Nu数分别在粗糙和光滑空间内作为Ra数的一项函数。整个空间的垂直热通量取决于所需的功率以保持下板在一个恒定的温度。实验证明，粗糙表面相较于光滑表面的热量传输增大了76%。为找到增强换热的原因，测量了对流流体在上板的温度波动，可以发现，在粗糙的空间中，(冷)热羽流的排放量大大增加，上表面粗糙使得热羽流进行横向的大尺度环流，在粗糙腔内的边界层上的温度波动减少。
为分析热羽流的成因，在上粗糙面采用了可视化温度和速度场的摄影技术，图5显示一个红色伞状羽流从冷端粗糙面产生，在近壁区大规模环流运动的特点类似于一个简单的剪切流，当它与正锥面相遇，平均流从表面发散。在椎体的下游侧，形成一个不利的压力梯度区域。这种逆向梯度产生的涡流，与大尺度环流方向相反。其相互作用使得热边界层与附近锥尖分离，使得热边界层形成热羽流，与此同时，内部的小涡旋也在槽内形成强烈的混合，这对边界层附近的局部温度也造成影响。
3.1.3. 实验结论
描述了一种在封闭空间中粗糙上下表面的对流实验。当V型槽厚度K远大于边界层厚度时，整个粗
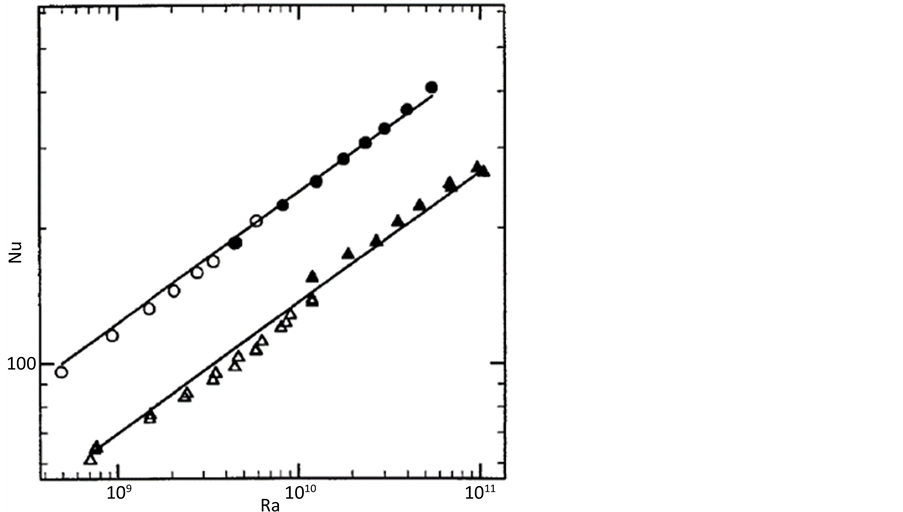
Figure 4. Nu and Ra log plots under smooth and rough surfaces
图4. 光滑和粗糙表面下Nu跟Ra对数图
Figure 5. Visualization of temperature and velocity fields
图5. 可视化温度和速度场
糙空间的热传导增加76%以上。流动显示和近壁面温度测量表明，大尺度环流在粗糙表面较之光滑表面会额外产生更多扰动，流动边界层受到一定程度的破坏，导致层流特性得到相对减弱或是层流流动转变为湍流流动，最终使得粗糙表面的平均传热效果得到增强。
表面粗糙度对于RB湍流的影响，其研究对对流湍流的性质提供了新的见解，在工程、地理和气象上也有更多大量的应用，但目前对于不同粗糙度对强化传热效果的影响，仍需要进行更丰富细致的实验。
3.2. 分区在热对流中强化传热
在RB对流对流换热强化研究中，揭示了一种新的机制，会导致更大的热量传送：即当垂直分区被插入到一个对流单元的隔离墙与冷却(或加热)板之间的间隙时，对流会变得自发组织更加一致，最终导致一个前所未有的热传输增强。特别是，当六个隔墙插入时，热通量可增加约30%。数值模拟显示当分区数到达28个时，热通量增强达比没有分区高2.3倍左右。
3.2.1. 实验介绍
实验在一个50 × 15 × 10 (cm)的矩形单元中进行，上下导板是用纯铜并在表面电镀镍。侧壁是由四个1.2 cm厚的有机玻璃组成。几个1.2 cm厚的有机玻璃隔板将矩形室分成若干子室，每个隔板与水平板留有2 mm高度的间隙，以保持每个子室与不分区时的系统拥有相同的纵横比，该结论已被Ahlers等 [12] [43] 通过研究得到。上板温度通过水冷调节，下板由嵌入的薄膜加热器在固定功率下加热，在持续流动边界条件下上下板保持一恒定温度，该温度由12个热敏电阻监测。系统流体采用平均温度31℃的介质水，对应的Pr = 5.3，Nu是在3.5 × 107 ≤ Ra ≤ 8.3 × 108的范围内进行测量。对于每个Ra数，系统都要稳定4~8小时以达到一个良好状态。同时，为减少周围环境的影响，整个系统包裹在几层聚苯乙烯塑料泡沫中。
直接数值模拟(DNS)也对该实验进行演绎，鉴于二维模拟所需模拟数值比三维模拟小得多，且详细的温度跟速度场在二维图中更容易获得，温度和速度等信息均直接可用，可轻易识别出复杂的物理机制，因此选用多个二维空间分区模拟，其中Pr数和Ra数均固定。数值代码基于不可压缩的Oberbeck-Boussinesq方程的有限差分法，限制方程如下：
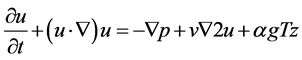
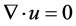
速度场在所有边界均服从无渗透、无滑移的边界条件；温度场是在其界保持绝热等温(无热通量)。运用投影算法的思想求解方程，空间导数近似由二阶中心有限差分法在交错网格中求得，由于隔板边界的复杂计算情况，采用高斯赛德尔迭代法解决压力泊松方程。
3.2.2. 结果与讨论
图6 [44] 显示了一个补偿努尔数的半对数图，对比Nu/Ra0.289的值发现当隔板数从0到6依次增加，Nu也表现出明显的增加，当n = 6时，Nu增加了32.7%。限制得增加反而提升了换热，值得注意的是，玻璃墙板的热效应是可以忽略不计的 [12] ，深入讨论热效率提高的原因，发现由于在对流过程中，浮力驱动引发了压力场的产生，最后流体在隔板间隙内水平推动，由于水平压力的下降，导致一个强大的水平射流产生，使冷或热流进入子单元室，从而实现了系统高效热交换。
由此可得出结论，分区热对流的强化换热是通过双效应引起的。首先，当隔板数N足够大时，每个子室中流体流动会更加连贯，从而得到更高效的热通量，但随着n的增多，隔板总的阻抗增加，导致整体热传输减少，因此必存在一个最佳隔板数。其次，由于射流的存在使导板附近流体温度梯度变大，导致边界层比传统RBC系统变薄约1/3。并且在这两种效应之间，薄间隙强水平射流是强化传热的主要因素，这种机制突出了间隙高度的重要性：对于适当高度的间隙，有一个最大的换热增强值。
因此，具有薄间隙连接相邻室的分区RBC系统，可产生不同的流型，导致热通量的增加。其中最重要的是产生的射流导致破坏对称分岔，冷热羽流被夹带到隔板两侧，形成一个水平压力梯度，之后的研究主要是关于改变分区壁厚以及对流区的纵横比对热量传输的影响，看怎样才能得到最佳换热的优化。
3.3. 约束引起对流换热强化
在湍流热对流的空间约束实验研究中发现，当对流腔室的宽度变窄，系统传热效率明显增加。在这里，依然利用经典的对流模型RB对流，该系统具有三个控制参数，Ra、Pr、纵横比 。Ra表征测量的
热驱动力，Pr测量粘性和热扩散的相对优势，纵横比 是对流室的几何形状和影响对流结构和动力学。由于在RBC主导的对流结构是大尺度环流(LSC)，但结论显示LSC几乎不影响系统整体热传输，相反，后者主要由热边界层确定，因此显著改变热量传输的唯一方式是直接扰乱热边界层。不同纵横比的对流室理论上可改变热边界层厚度，随着纵横比减小，系统摩擦阻力会增加从而在侧壁增强换热，研究揭示了侧向约束湍流流动引起的增强换热过程。
3.3.1. 实验
实验研究利用五个矩形对流室，其高度和长度均固定为12.6 cm，宽度变化范围从7.56到1.27 cm，垂直面的纵横比分别为0.6，0.3，0.2，0.15，0.1。Nu测量范围在8.6 × 107 ≤ Ra ≤ 2.5 × 109，以保持平均温度Tc为40˚(Pr = 4.3)。为降低环境温度波动的影响，对流室包裹几层保温绝热层，放置在恒温器中。
同时，相应的直接数值模拟(DNS)采用Boussinesq方程的有限体积求解非等距网格在坐标方向以及交错网格对应三个速度分量 [45] 。笛卡尔几何构型是离散的，因此网格间距是在x-z平面保持垂直和水平一样，水平和垂直壁面的边界层也能得到解决。网格间距在几何中心是等距的。对配置文件进行后期分析，发现所有相关尺寸都能得到完美解决。
3.3.2. 实验结果和分析
如图7，显示了一个不同Ra数下，Nu和Γ的对数图，不同纵横比Γ下，Nu随着Γ的减小而呈现增大趋势，考虑到在高度受限空间内，阻力增大会降低流体流速从而抑制垂直热量传输，但实验却显示了相反的结果，因此可预测在 减小时有什么减小了阻力增大的影响，因此，我们进行接下来的试验。
在保持Pr和Ra数固定的实验下分析不同纵横比 的影响，如图7显示了纵横比为1/2 (图8(a))和1/8(图8(b))下距离水平面z ≈ 2δth下的瞬时速度场和水平温度场图，结果表明对于纵横比小的流体，当热羽流朝向冷羽流时，会发生更多的碰撞，融合，然后上升，因此可携带更多的热量，使得热量传输不再局限于周边，而发生在整个对流室中。
基于以上分析，可得出以下结论：首先，约束导致壁面的摩擦阻力增加，从而显著减弱了LSC最终在高度受限条件下抑制了它，使得热羽流影响了整个边界层 [45] 。再加上在边界层内羽流形态的变化，导致更加连贯和具有活力的羽流，整体Nu因此得到提高。几何约束效应为影响湍流边界层的原因提供了新的范例，目前对约束引起对流换热的加强还有许多实际问题需要作出研究，例如在微电子工业中的冷却装置的设计。
(a) (b)
Figure 6. The Compensated logarithmic graph of Nu/Ra0.289
图6. Nu/Ra0.289补偿对数图
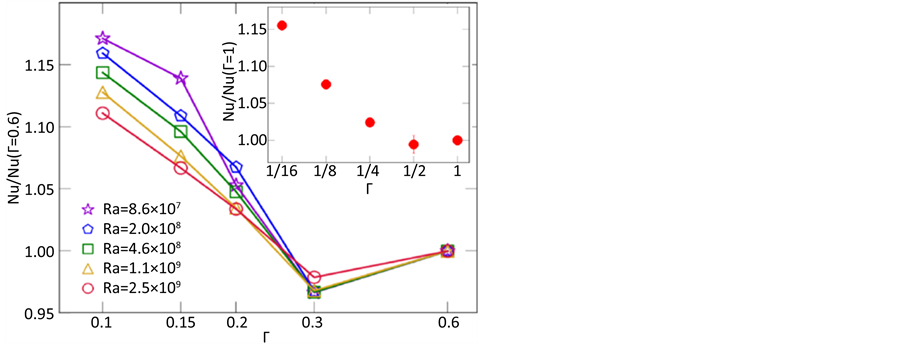
Figure 7. Logarithm of Nu and Γ under different Ra numbers
图7. 不同Ra数下Nu与Γ对数图
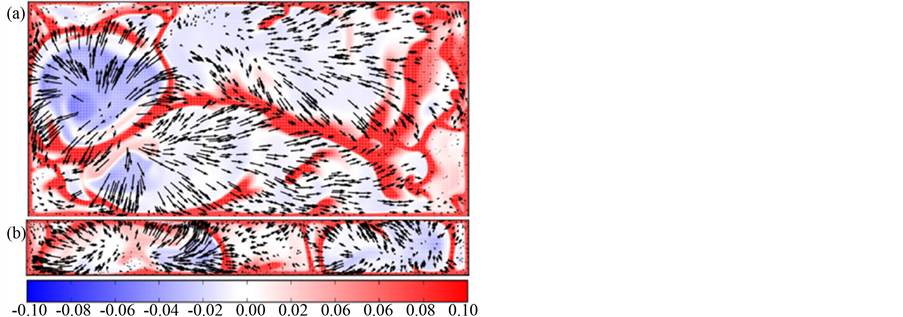
Figure 8. Velocity and temperature fields of fluid with different aspect ratios
图8. 不同纵横比流体速度场和温度场
4. 工程应用展望
RB湍流对流强化技术在目前工程上取得了很多重要成果，本节筛选代表性的工程应用做简要介绍。
4.1. 在冻土路基中的应用
由于全球气候转暖和人类工程活动日益加剧，多年冻土退化加快，这使得多年冻土区的道路工程建设更加困难。在自然界温度季节变化中，碎石层能起到“热半导体”的作用。如图9，冬季时，下层冻土温度高于上层土壤，会产生类似于Rayleigh-Benard对流下板热上板冷的条件，从而产生对流，热交换得到加强，冻土中热量大量向周围空气散发；夏季时情况相反，上板热下板冷，较轻的热空气在上，无对流产生，热对流主要通过传导进行，而碎石层中碎石之间接触面积小，使导热系数大大降低。从而碎石层在冬季放热加强，夏季吸热减少，造成“热半导体”的作用。年循环的结果就是冻土放热，使地表温度降低。
目前的研究主要在于如何加强碎石层的“热半导体”作用，实验发现，当碎石层倾斜放置时，会产生烟囱效应，在开放条件下，冬季，由于烟囱效应，产生上升热流，使岩屑堆上部覆盖的积雪产生融洞，同时从岩屑堆下部吸入冷空气；夏季，冷空气沉入岩屑堆下部，其结果导致岩屑堆温度最低，植被稀疏
Figure 9. Semiconductor effect of the crushed stone layer
图9. 碎石层的半导体作用
[46] 。同时，开放碎石层依靠外部低压气流引起的强迫对流，大大增加了碎石层的冷却效应。
4.2. 各类异型强化换热管的应用
目前应用的主要异型强化换热管有螺旋槽纹管、横纹槽管、波纹换热管以及翅片管等。异型强化换热管的强化换热原理就是利用各种管的特殊结构产生涡旋，扰乱减少了边界层厚度，增大地热阻区，从而增强换热。螺旋槽纹管和横纹槽管广泛应用于各种形式的换热器、余热锅炉中，翅片管主要应用在管壳式换热器及空冷器中。除上以上几种异型管，还有旋流管、缩放管也利用其加强换热的特点可用于实际应用。
4.3. 天然液化气储罐安全性问题
液化天然气作为一种优质洁净的能源，应用范围很广，普及率也非常高。但作为一种易燃易爆品，其运输与储存的安全性问题，更需要加以更多的关注。研究表明，液化天然气储运失稳事故的发生主要原因是由于产生涡旋。对于该安全性问题的研究，从非线性动力学角度出发，可以建立RB对流模型。
储罐内的液化天然气由于各种原因产生分层，在密度差的影响下，储罐内分气相区和液相区，液相区又分为分层区和主流区，密度大的液化天然气在液相区底部，上下层的自然对流被限制在各自的层内，相邻的两层液体之间会产生一个非常薄的液-液界面，它对两层液体的传热产生很大影响。
如图10，用Rayleigh-Benard对流模型可得出流体运动主要由长宽比、Pr数和Ra数三个参数决定，在这里，较小的外部热流流量可导致较强的非稳态自然对流，从而产生涡旋，所以在液态天然气运输过程中，可通过改变上面三个参数，减小液态天然气分层，最终有效减小储运失稳事故。
5. 小结
Rayleigh-Benard对流现象是日常生活中一种常见的热对流现象，且其湍流对流流动性质是由多个无量纲参数控制，其流动机制和传热机制非常复杂。目前通过大量的物理模型实验和数值模拟的研究，人们对RB对流已有了一定程度的认识和理解。本文简述了目前国内外学者提出的RB对流强化换热技术的各类方法并进行归纳和总结，并描述其代表性的工程应用，主要结论及对比结果见表1，旨在呈现各类强化手段的原理和存在的不足，以便进一步推动该研究方向的发展。未来研究工作的方向可能有：对所述的各种强化手段进一步明确相关参数的影响，使其换热率得到最大程度的优化；研究在不同外力条件
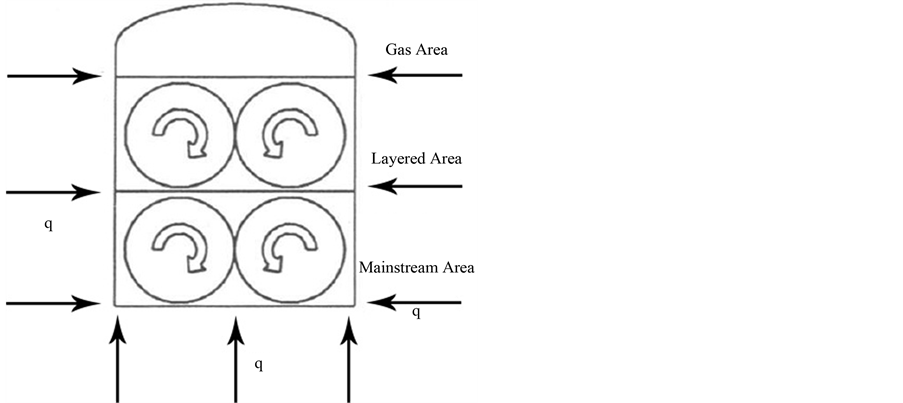
Figure 10. Schematic diagram of natural convection of liquefied petroleum gas
图10. 液化天然气储罐自然对流示意图
Table 1. Comparison of various methods
表1. 各种方法的比较
下的混合流体RB对流的特性；探讨各种初始耦合条件对流动换热结构的影响；以及多组分流体在各种热边界条件下的稳定性与动力学特性。希望通过这些研究，可以为本文所述的各种方法找到互补耦合的优化组合模式，深入理解RB对流在复杂外力及边界条件下的流动换热机理，从而将其更好的应用到实际工程实践中去。