1. 引言
生物力学研究表明，人类和其它生物的运动之所以自然、优美、高效，原因是人类和生物极善于利用躯体各部分的动力耦合来实现运动能量的传递，达到整个机体的高度协调。因此，对基于动力学耦合驱动原理的欠驱动机器人展开研究，将会促进机器人从呆板机械的运动向接近人体或生物的动力协调运动发展。由于欠驱动系统的高度非线性、参数摄动、多目标控制要求及控制量受限等原因，系统的动特性显得非常复杂，其一般力学特性，包括其固有运动在内，理论解析上还很不明确 [1] 。作为欠驱动机器人家族中的一员，单杠体操机器人可以简化成由一个被动关节和多个主动关节组成的欠驱动连杆系统模型。近年来，国内外相继报道了许多以该类机器人为对象的研究成果 [2] - [8] 。
在国内外早期关于体操机器人的研究中，大都采用Acrobot的欠驱动两关节体操机器人模型 [9] [10] [11] 。Acrobot是一种具有2个自由度和1个主动关节的两关节机器人，它能简单的模拟体操运动员在单杆上的摆起、倒立、大回环等体操动作，其第一个关节是非驱动的，模拟了体操运动员的腕关节，第二个关节是驱动的，模拟了体操运动员的髋关节。随着研究的深入，目前较多采用的是三关节体操机器人模型，其具有3个自由度和2个主动关节，其中肩关节和髋关节为主动关节，腕关节为被动关节，是一种典型的欠驱动机器人 [8] [12] 。该机器人可以有效地模拟体操运动员肩关节和髋关节的主动控制作用，相比于Acrobot，三杆体操机器人具有更强的非线性和耦合性，其控制具有高度的复杂性和非线性，可用来检验控制理论和控制方法在类似复杂控制系统的有效性 [13] [14] [15] 。
四关节欠驱动体操机器人具有4个自由度和3个主动关节可有效模拟运动员的肩关节、髋关节和膝关节的主动控制作用。膝关节的加入使得单杠体操机器人能做出更加复杂的体操动作，因此，四关节单杠体操机器人能更好地反映真实体操运动员的肢体运动，当然，这类机器人也具有更复杂的非线性特性，目前国内外尚鲜有相关研究成果报道。4关节单杠体操机器人的运动控制研究，对于进一步实现更逼真的类人体操机器人具有重要的意义。本文以4关节体操机器人在单杠上倒立稳定运动作为控制目标，提出了一种采用LQR的平衡控制方法。
2. 动力学分析与建模
2.1. 物理模型
四关节体操机器人能够被抽象为一个如图1所示的由4节连杆、4个关节连接构成的刚体。第i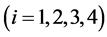
个连杆分别定义为机器人的手臂、躯干、大腿和小腿，第i
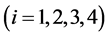个关节分别对应为腕关节、肩关节、髋关节及膝关节。
，
，
，
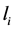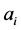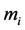分别定义为第i
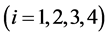个连杆的长度、质心–轴心距、质量以及以质心为转轴时的转动惯量，
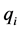为第i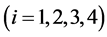
个关节的角度，角度的正方向为逆时针方向。
4关节欠驱动体操机器人，腕部的旋转为完全不受限的旋转，转角范围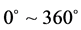
，肩关节、髋关节和膝关节不能做完整的旋转。采用拉格朗日力学的方法建立体操机器人的动力学模型，拉格朗日运动方程式为：
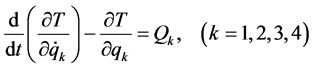(1)
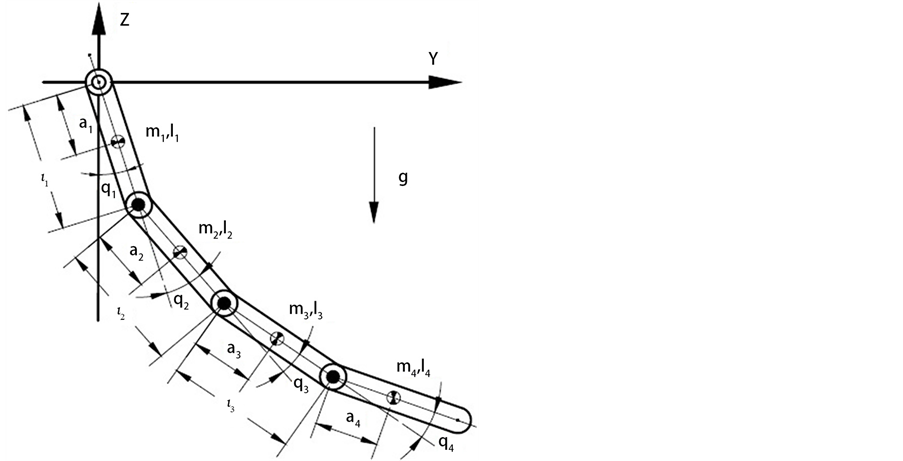
Figure 1. Physical model of four-link gymnastic robots
图1. 四关节体操机器人物理模型
式中，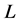
为拉格朗日算子；
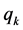为系统的广义坐标；
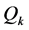称为系统的广义外力。求解拉格朗日算子，可得到4关节欠驱动体操机器人的动力学模型：
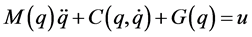(2)
式中，
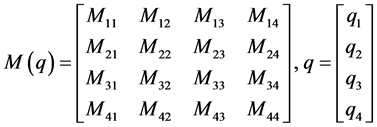
其中，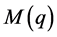
称为惯性矩阵，是对阵正定矩阵，
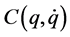是离心力矩阵，
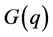表示加在机器人上的重力项。
的表达式见附录。
另外，由于在广义坐标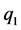
上无外力作用，则下式成立：
(3)
因此，4关节欠驱动机器人是典型的多输入(
)多输出(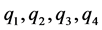
)的非线性多变量系统，在系统的各变量间存在有较强的耦合作用。
2.2. 倒立平衡点附近状态空间模型推导
4关节欠驱动体操机器人的平衡是把机器人稳定在垂直倒立的不稳定平衡区。虽然体操机器人在整个运动范围内是非线性的，但在其垂直向上的平衡点附近，体操机器人的动力学模型可以采用线性化的近似模型来表示。
由方程式(2)可以推导出：
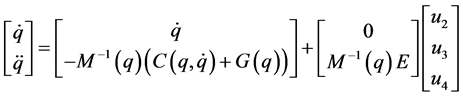(4)
其中，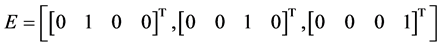
。
定义状态变量
如下：
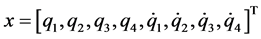(5)
则可以将式(4)写成：
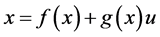(6)
机器人在垂直向上的倒立位置时，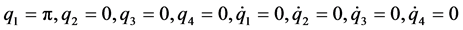
，则可定义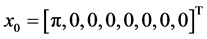
。在倒立平衡点
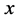附近对系统进行线性化处理，可得到体操机器人系统的状态空间描述为
(7)
式中，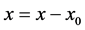
，
，
，
，
。
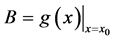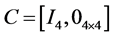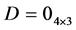3. 倒立平衡控制
体操机器人倒立稳定控制的目标就是控制机器人在垂直向上不稳定平衡点附近达到并保持倒立状态，但该过程是一个动态平衡，因为机器人在平衡位置是不稳定的，因此需要设计一个平衡控制器才能实现这一目标。
LQR(Linear Quadratic Regulator)即线性二次型调节器可得到状态线性反馈的最优控制规律，易于构成闭环最优控制。由式(7)的状态方程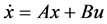
确定最佳控制向量
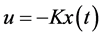(8)
的反馈矩阵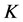
，使得下述二次型性能指标最小
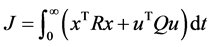(9)
式(8)中，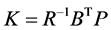
，其中，对称矩阵
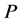为式(10)所示的定常黎卡提(Ricatti)矩阵微分方程
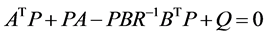(10)
的唯一正定解。此外，矩阵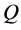
和
为加权矩阵，其确定了误差和能量损耗的重要性。
4. 数值仿真
为了验证LQR平衡控制器的控制效果，使用MATLAB进行仿真。体操机器人模型的参数设置如表1所示。
基于表1的机器人模型参数，由式(7)可求得机器人线性化系统的矩阵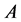
，
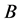如下：
,
.
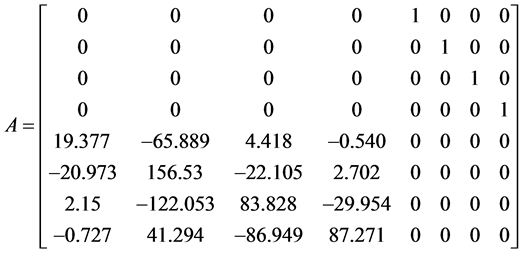将求得的系统矩阵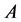
，
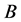代入式(10)中，选取
，
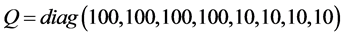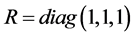，可得到状态反馈增益矩阵K为
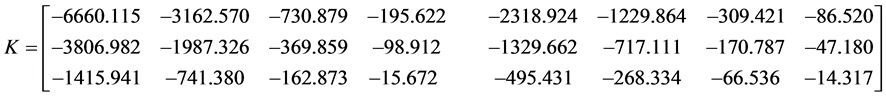
假设系统初始状态分别取下式(11)所示的值，
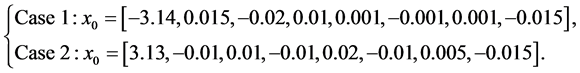(11)
利用求得的LQR控制器参数，仿真可以得到图1~6所示的机器人倒立稳定的仿真曲线，其中，图1~3
Table 1. Model parameters of gymnastic robots
表1. 体操机器人模型参数
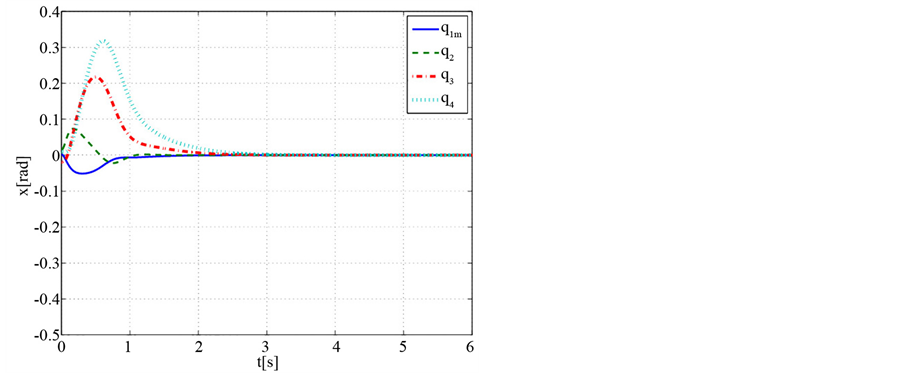
Figure 2. Angular variation of balance control (Case 1)
图2. 平衡控制的角度变化(Case 1)
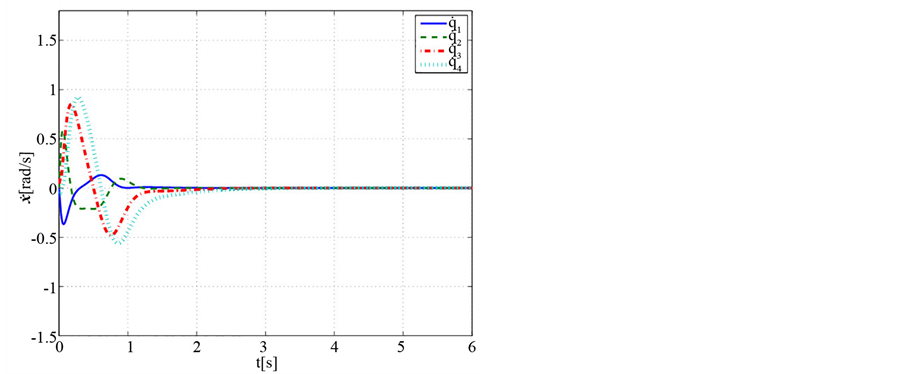
Figure 3. Angular velocity variation of balance control (Case 1)
图3. 平衡控制的角速度变化(Case 1)
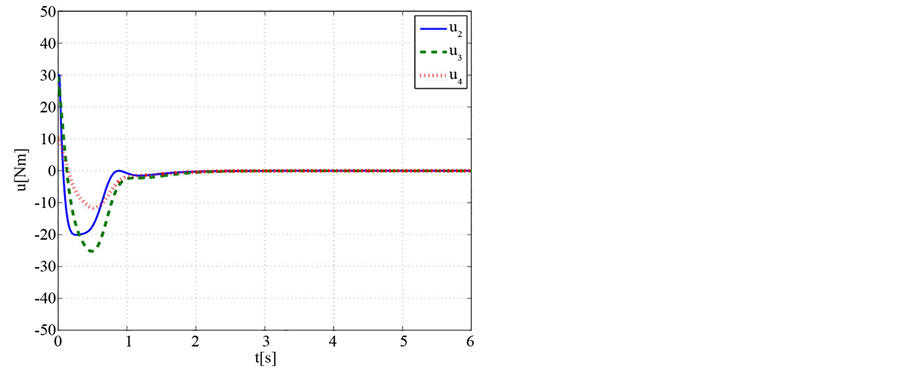
Figure 4. Torque variation of balance control (Case 1)
图4. 平衡控制的力矩变化(Case 1)
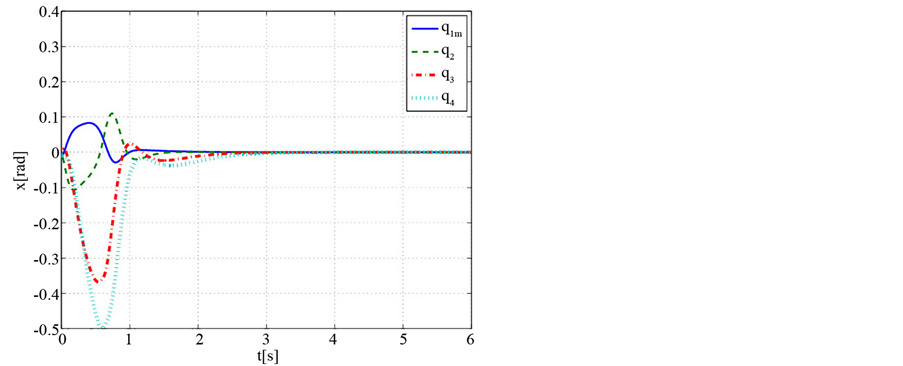
Figure 5. Angular variation of balance control (Case 2)
图5. 平衡控制的角度变化(Case 2)
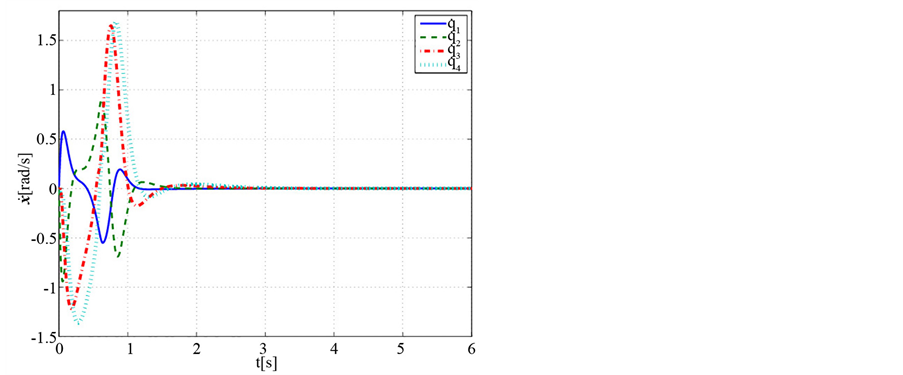
Figure 6. Angular velocity variation of balance control (Case 2)
图6. 平衡控制的角速度变化(Case 2)
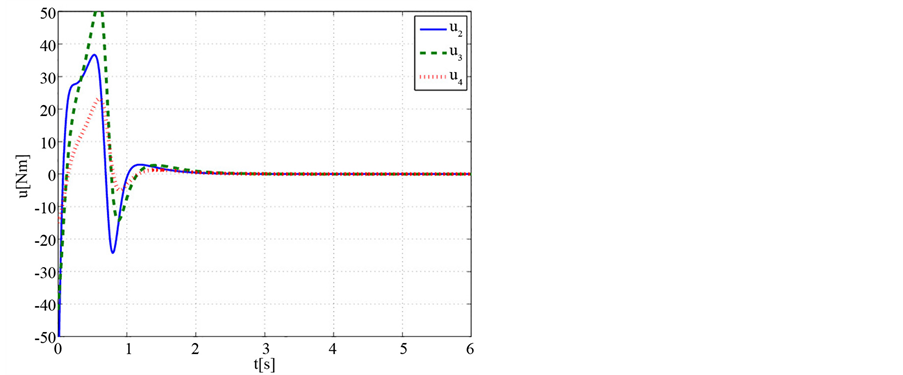
Figure 7. Torque variation of balance control (Case 2)
图7. 平衡控制的力矩变化(Case 2)
为取式(11)中的Case 1所示的初始状态所得到的响应曲线，图4~6为取式(11)中的Case 2的初始状态所得到的响应曲线。图1和图4分别显示两种状态下的4个关节角度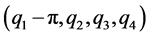
的变化曲线，图2和图5分别为4个关节角速度
的变化曲线，而3个主动关节的控制力矩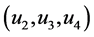
的变化曲线分别如图3、图6、图7所示。仿真结果表明，机器人即使在不同的初始条件下，不改变控制器参数，基于LQR的控制器仍然能够使系统达到倒立稳定。
5. 结束语
本文在分析并建立四关节欠驱动单杠体操机器人的数学模型及其在倒立平衡点附近线性化方法的基础上，基于LQR设计了一种控制器以实现对该机器人直体倒立的稳定控制，仿真实验验证了该控制方法的有效性。本文的工作为下一步实现四关节单杠体操机器人更加复杂的运动动作控制奠定了基础。
基金项目
教育部留学回国人员科研启动基金项目，上海交通大学新进青年教师启动计划基金项目。
附录
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
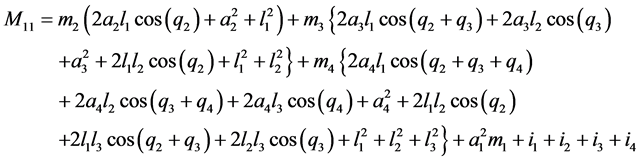
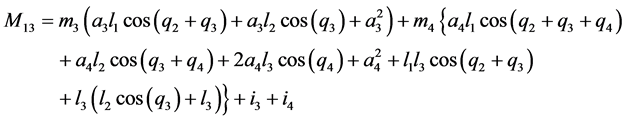
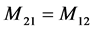
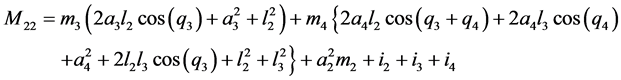
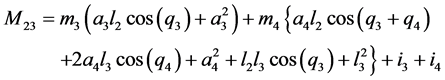
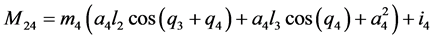
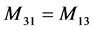
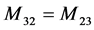
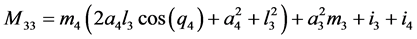
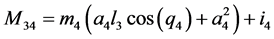
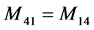
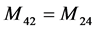
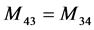
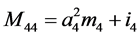
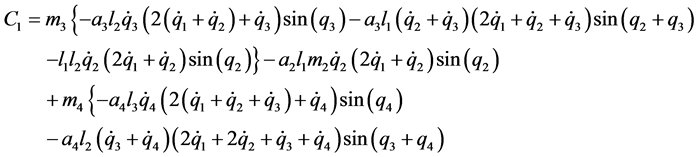
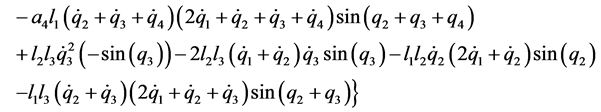
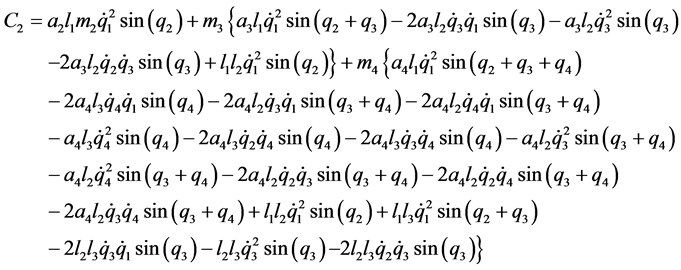
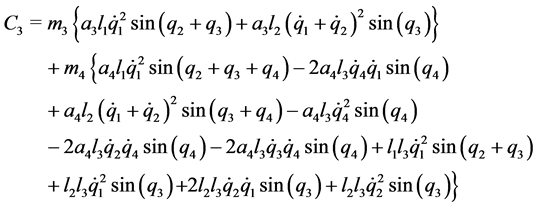
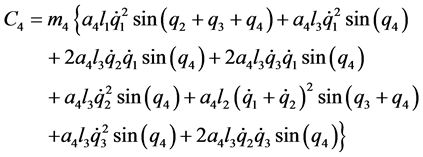
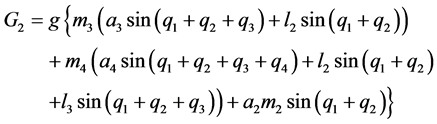
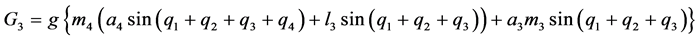
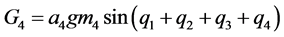