1. 概述
目前针对交通机电工程检测方案，尤其是面向网络结构系统，一般仅关注抽样比率及随机抽取方法，而对其效率和误差指标的研究却很少涉及；因此，确认最终检测结论的准确性与合理性仍有相当多的疑问亟待澄清。
本文通过一个简化版的13站点区域性环网系统，以每个站点的设施为检测组群，这些设备可以是通信系统的接入装置，也可以是监控系统的路侧设备集中点，还可以是收费系统的闸口设备等。利用田口玄一正交法 [1] 分析各种检测方案的筛选过程以及相应效率的评估取舍。
2. 田口正交法分析
下图1为本文所举案例的设施分布示意，自编号A至N共有13个区域站位，设置有直通和互通两种类型；站位之间标注的数字代表相邻的距离，以均匀行程时间(分钟)衡量。依据《公路工程质量检验评定标准》 [1] 抽样不低于10%的规则，本案例中同时设置15%和0% (即该点不检测)共计3个等级水平作为调控参数。从而，进行本案例分析时的期望目标为10%的抽样比；望小值则为检测工作时长，期望能尽量压缩不必要的时间损耗；进而在满足规则要求的前提下，充分提高检测效率，并且通过判别相关结论的误差百分比，确认最优选择的可信性。
计算各种情况所需平均时长为：直通站(Z型)进出费时4分钟，互通站(Y型)进出费时10分钟。① 水平检测耗时45分钟，抽样率15%；② 水平检测耗时30分钟，抽样率10%；③ 不检测，抽样率0%。
当只有一个工作组投入检测时，按照最短路径选择排列顺序，单程最短路径为：A-B-C-D-E-F-G-H-E-J-K-L-C-M-G-H-E-N；其中有3个站点需要重复经过1次，E站点则需要经过2次，途中共费时211分钟。若每站均按15%抽检率计算，则总计需要T = 45 × 13 + 5 × 10 + 8 × 4 + 211 = 878分钟(约15小时)。实际制定检测方案时，是希望在减少工作时间的同时能够保有相对较高的检测覆盖率，以此提升检测结论的可信性。
为了简化问题，假设可以从编号A和N两个起讫点分别执行点对点的单任务检测，则将各种最短路径统计于下表，从表1中可以看出，N端站点共有9次被选作起讫点，是此次任务的关键节点位置，若在实际计划时，则应是检测组住宿和内业工作的首选场所。
鉴于上述情况，选择采用田口正交法
表进行统计分析。利用该表只需进行27次有效观察，就能代表具有13个因素(站位数)、每因素含有3水平(三种抽样概率)组合成的1,594,323次普通推算可能。将表1数据代入表2计算。
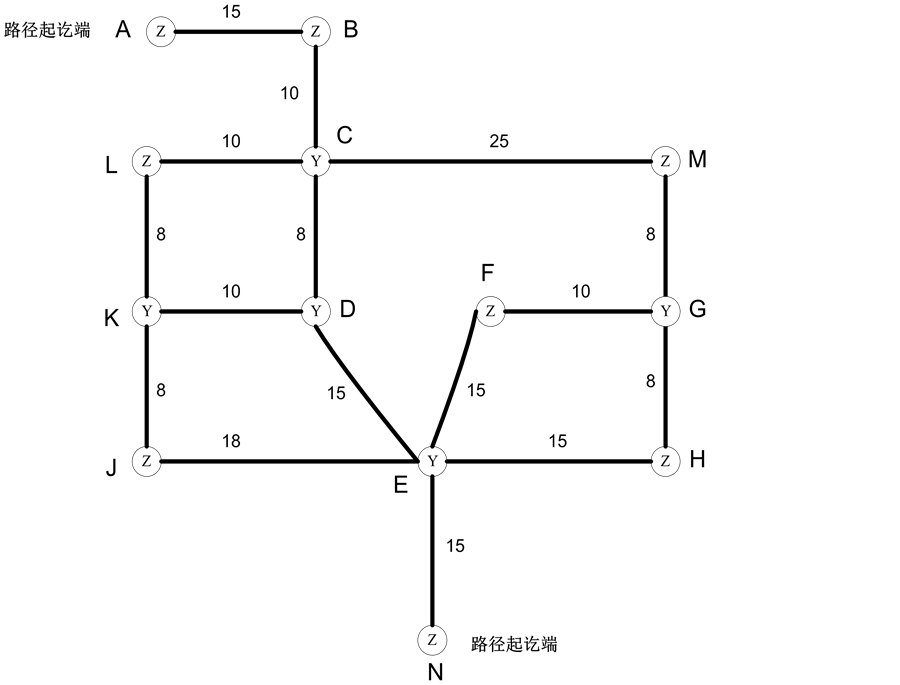
Figure 1. Distribution of electrical-mechanical engineering testing site map
图1. 机电工程检测站点分布示意图
Table 1. Single task shortest path summary table
表1. 单任务最短路径汇总表
表2. 田口正交法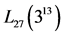
表 [1]
Continued
根据表2的计算结果分析如下：
(1) 13个站点因素平均值的极差都是15分钟，这说明站点之间不存在特别差异，对检测结果的影响是均衡的，因此可以任选其一作为系统的代表样进行检测。
(2) 27次推算结果的时长极差为726分钟，表明抵达不同站点的路径与该站点抽样率所构成的组合影响显著；即,站点位置和检测时间很重要。
(3) 方案1是对100%站点进行全部15%的抽样检测，其时长和抽样误差百分率分别为19.9%和0%，但费时最久(1004分钟)；而方案3虽然时长(278分钟)最短，但误差较高；所以这两个方案一般不予考虑。
(4) 通过比选，方案4作为首选，其检测时长686分钟，时长误差19.7%，抽样误差62.0%；方案2 作为次选，其检测时长869分钟，时长误差21.7%，抽样误差20.9%。
(5) 综合上述分析，推荐方案4，其抽样概率为9.2%，接近10%的期望目标。该检测方案类型为：A1B2C2D2E1F1G1H2J2K2L3M3N3，即第1和第5~7共4个站进行15%的抽样，第2~4和第8~10共6个站进行10%的抽样，第11~13计有3个站不检测。按照单行程A-B-C-D-E-F-G-H-E-J-K-L-C-M-G-H-E-N路径进行框算，总时长近似为686 × (878/1004) = 600分钟(约10小时)，比初始估算时间(约15小时)缩短了1/3。方案2的抽样率达到11.5%，且误差较小，但检测时长和误差均低于方案4的指标。因此，基于效率和准确度平衡的角度，以方案4为优选，方案2作为备选。
3. 抽样误差分析
按照《公路工程质量检验评定标准》 [2] 要求，机电系统关键项合格率为100%，次要项目合格率需达到90%以上，现场抽样数不应少于3个。
按不重复抽样公式计算如下：
若：
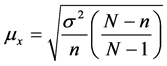
其中
为总体标准差，此处以样本标准差代替(设为2.4%)，那么，当N值很大时，计算公式可近似为：
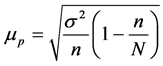
其中：标准差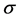
设为2.4%，n为抽取个数(设为3个)，n/N为抽样比率(设为11.5%)，代入计算：
因此，当每站点抽检不少于3组套设备时，依据前面案例分析数据的结论，其中备选方案2的随机抽样误差为0.4%；优选方案4的误差为1.0%。其他各组如下表3。
按照不重复抽样条件，针对期望目标为总体不低于10%抽样率的各类型方案误差均很低，系统误差很小，完全能够达到现场控制质量的目标，并且随着抽样数量的增加，相应的误差会更加趋向减小。
4. 结语
经上述案例分析，能系统地证明，按照《公路工程质量检验评定标准》 [2] 要求，既便采取较高风险的小比率抽样方式，但通过对检测方案的计划、筛选、抽样频次等因素的高效组织，同样能够极大地改善检验结果的准确度和效率。
Table 3. Non repeated sampling error calculation summary table
表3. 不重复抽样误差计算汇总表
因此说，任何节省成本的努力都必须基于科学严谨的方案设计；并且，当能够有效地控制客观误差，也就可以确保检测结论的可靠性。