1. 引言
艾滋病是由人类免疫缺陷病毒(HIV)感染人体后,导致被感染者免疫功能的部份或完全丧失,CD4+ T细胞数目减少,继而发生机会性感染、肿瘤等最终导致死亡的一种综合症。
据世界卫生组织统计,截至2013年年底,全球约有3500万名艾滋病病毒感染者。2013年全球新增的艾滋病病毒感染者约210万人。
目前,人类正在面临着艾滋病感染的长期而严峻的威胁,对艾滋病的发病机理、传染规律和防治策略研究的重要性日益突出,而HIV潜伏库的形成机制以及彻底清除潜伏HIV的策略正是当下国内外研究的热门话题。
迄今为止,许多国内外科研人员已经在基本的HIV病毒动力学模型基础上考虑了潜伏感染因素、药物治疗等因素。2015年,Khan等人研究了潜伏细胞的激活与细胞凋亡的关系,并指出宿主细胞凋亡信号可能使潜伏病毒暴露从而清除潜伏HIV [1] 。刘叔文等人在2015年发表了一篇相关的医学文章,主要研究了HIV潜伏库的形成机制以及将潜伏细胞激活的激活剂,总结了将整合后潜伏的病毒从机体彻底清除,实现HIV的根本治愈的方法 [2] 。但是,要想彻底清除潜伏HIV,必须了解HIV潜伏感染机制。
因此,在这些研究的基础上,本项目从HIV潜伏感染机制着手,在潜伏感染模型中考虑了潜伏感染细胞以一定比率恢复成健康T细胞,T细胞以Logistic形式增长以及药物治疗因素,然后求出了模型的两个平衡点,分别是未感染病毒平衡点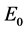 和感染病毒平衡点
和感染病毒平衡点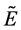 ,并从理论上研究了系统在这两个平衡点的稳定性。此外,根据目前的一些医学数据对模型进行了数值模拟,验证了在未感染病毒平衡点和感染病毒平衡点处系统的稳定性。最后将不同的模型进行比较,得到了更真实的HIV感染过程,从而研究HIV的感染机理。
,并从理论上研究了系统在这两个平衡点的稳定性。此外,根据目前的一些医学数据对模型进行了数值模拟,验证了在未感染病毒平衡点和感染病毒平衡点处系统的稳定性。最后将不同的模型进行比较,得到了更真实的HIV感染过程,从而研究HIV的感染机理。
2. 基于Logistic增长、潜伏感染和药物治疗的HIV模型
 (2-1)
(2-1)
其中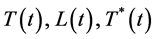 和
和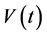 分别为在t时刻未感染的T细胞的浓度,被感染后潜伏的T细胞的浓度,受感染的T细胞的浓度和具有传染性的病毒颗粒的浓度;
分别为在t时刻未感染的T细胞的浓度,被感染后潜伏的T细胞的浓度,受感染的T细胞的浓度和具有传染性的病毒颗粒的浓度;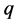 为潜伏感染细胞转化为健康细胞的转化率;
为潜伏感染细胞转化为健康细胞的转化率;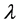 为产生健康T细胞的速率;
为产生健康T细胞的速率;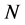 为每个感染T细胞释放病毒的数量;
为每个感染T细胞释放病毒的数量;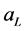 为易感T细胞潜伏的概率;
为易感T细胞潜伏的概率;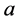 为潜伏T细胞被激活的速率;
为潜伏T细胞被激活的速率;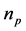 为蛋白酶抑制剂的药效;
为蛋白酶抑制剂的药效;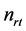 为逆转录酶抑制剂的药效;且初始条件为
为逆转录酶抑制剂的药效;且初始条件为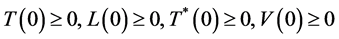 。
。
该模型考虑了药物治疗、T细胞以Logistic形式增长和具有潜伏感染细胞,并且还考虑了潜伏感染细胞以一定比率恢复到易感细胞的生物学机理 [3] 。
3. 模型平衡点
首先,模型(2-1)有一个未感染平衡点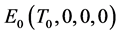 。
。
其中,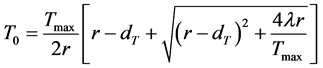 。
。
接着,我们定义基本再生数 [4]
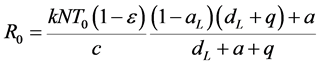 。
。
其中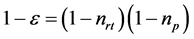 。
。
当基本再生数 时,平均每个病毒在它的存活期间要感染小于一个的T细胞,所以HIV病毒可以清除;当基本再生数
时,平均每个病毒在它的存活期间要感染小于一个的T细胞,所以HIV病毒可以清除;当基本再生数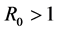 时,HIV病毒将继续感染健康T细胞,R0越大,病毒感染也就越快,此时病毒感染无法控制。
时,HIV病毒将继续感染健康T细胞,R0越大,病毒感染也就越快,此时病毒感染无法控制。
此外,当基本再生数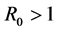 时,模型(2-1)存在一个感染平衡点
时,模型(2-1)存在一个感染平衡点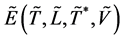 。
。
其中:
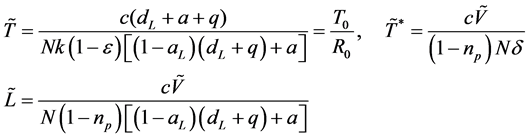
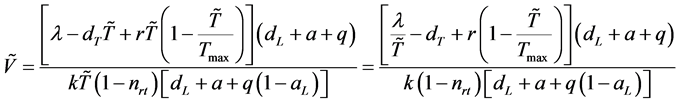
因为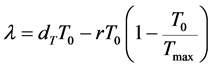
所以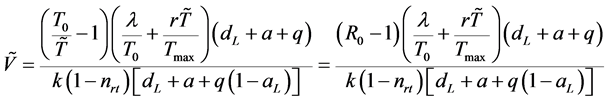
4. 解的非负性与有界性
在初始条件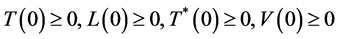 下,模型(2-1)存在唯一非负解,并且此解是最终有界的。
下,模型(2-1)存在唯一非负解,并且此解是最终有界的。
证明:由微分方程解的存在唯一性定理 [3] 知,模型(2-1)在非负初始条件下存在唯一解。
解的非负性:
可知: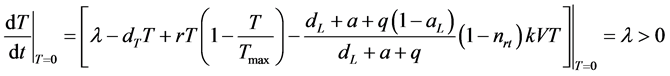 ,所以对于所有
,所以对于所有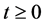 都有
都有 。
。
同理有: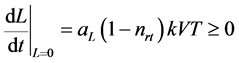 ,对于所有
,对于所有 都有
都有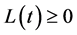 。
。
假设存在 ,使得
,使得 ,从而
,从而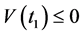 ,由于
,由于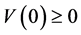 则存在
则存在 使得
使得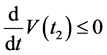 。
。
此时,当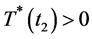 ,则
,则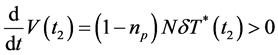 ,与假设所得到的结果矛盾;当
,与假设所得到的结果矛盾;当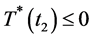 ,则
,则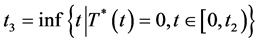 ,
,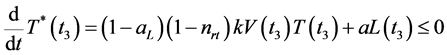 。
。
因为 ,所以
,所以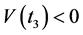 。由于
。由于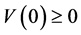 ,则存在
,则存在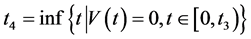 ,这与假设中定义的
,这与假设中定义的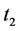 相矛盾;因此,假设不成立。
相矛盾;因此,假设不成立。
解是最终有界的:
可知: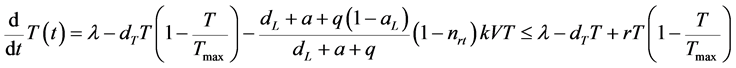 。因此:
。因此: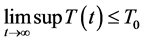 。
。
令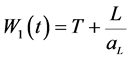 ,沿模型解的方向求导得到:
,沿模型解的方向求导得到:
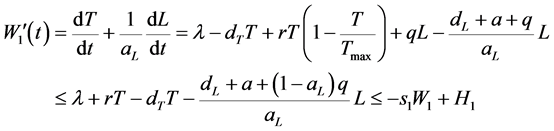
其中,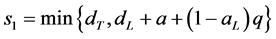 ,
,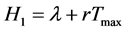 。显然
。显然 最终有界,又
最终有界,又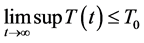 ,因此
,因此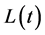 最终有界,记为
最终有界,记为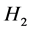 。
。
同理,得到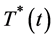 、
、 最终有界,记为
最终有界,记为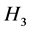 、
、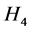 。
。
令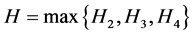 ,则当时间
,则当时间 充分大时有
充分大时有 ,即模型(2-1)的解最终是有界的。
,即模型(2-1)的解最终是有界的。
令 易知模型(2-1)的解都在
易知模型(2-1)的解都在 中并且
中并且 是系统的正向不变集。
是系统的正向不变集。
5. 平衡点的稳定性
5.1. 未感染平衡点的局部稳定性
定理1当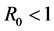 时,未感染平衡点
时,未感染平衡点 是局部渐近稳定的。
是局部渐近稳定的。
证明:模型(2-1)在未感染平衡点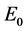 处的Jacobi矩阵为
处的Jacobi矩阵为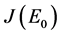 ,令
,令 ,即
,即
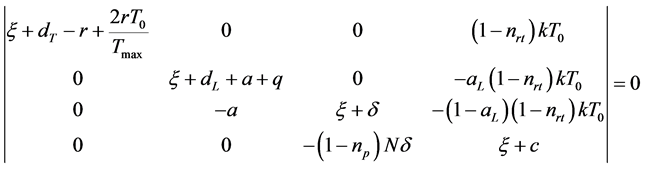
其中,
1) 
2) 
因为 ,
,
即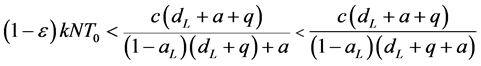 。所以
。所以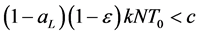 。
。
因此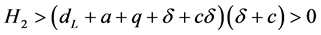 。
。
3) 
所以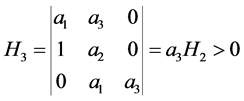 。
。
因此,由Routh-Hurwitz判据 [5] 可知特征方程的所有根都具有负实部。
综上可得,当 时,未感染平衡点
时,未感染平衡点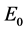 是局部渐近稳定的。定理1得证。
是局部渐近稳定的。定理1得证。
5.2. 未感染平衡点的全局渐近稳定性
定理2 当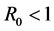 时,未感染平衡点
时,未感染平衡点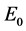 是全局渐近稳定的。
是全局渐近稳定的。
证明:构造Lyapunov函数

计算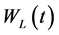 的导数,得到:
的导数,得到:
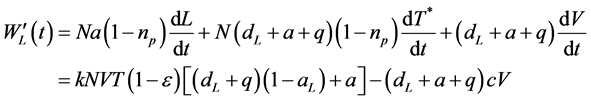
由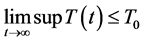 得
得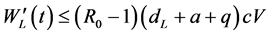 。
。
当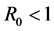 时,有
时,有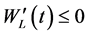 ,当且仅当
,当且仅当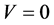 或
或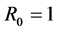 且
且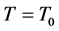 时,
时,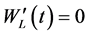 。
。
因为集合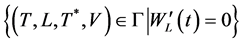 的最大正向不变集是
的最大正向不变集是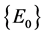 ,根据Lasalle不变原理 [6] 和Lyapunov稳定性定理 [7] 知,未感染平衡点
,根据Lasalle不变原理 [6] 和Lyapunov稳定性定理 [7] 知,未感染平衡点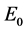 是全局渐近稳定的。定理2得证。
是全局渐近稳定的。定理2得证。
5.3. 感染平衡点的局部稳定性
定理3当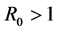 且
且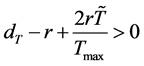 时,感染平衡点
时,感染平衡点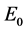 是局部渐近稳定的。
是局部渐近稳定的。
证明:
感染平衡点 处的Jacobi矩阵为
处的Jacobi矩阵为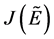 ,令
,令 ,即:
,即:
因为 ,所以
,所以 。
。
1) 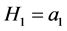
因为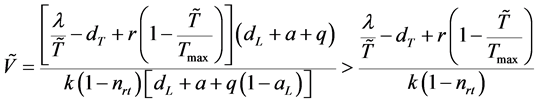 ,所以
,所以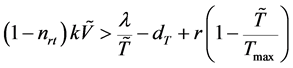 。
。

2) 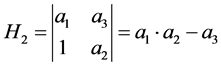
并且
于是:
3) 
已知 ,因此
,因此 。
。
同理
 ,
,
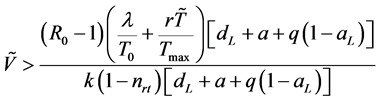 ,
, 。
。
因此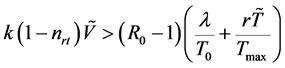 ,
,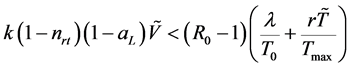 。
。
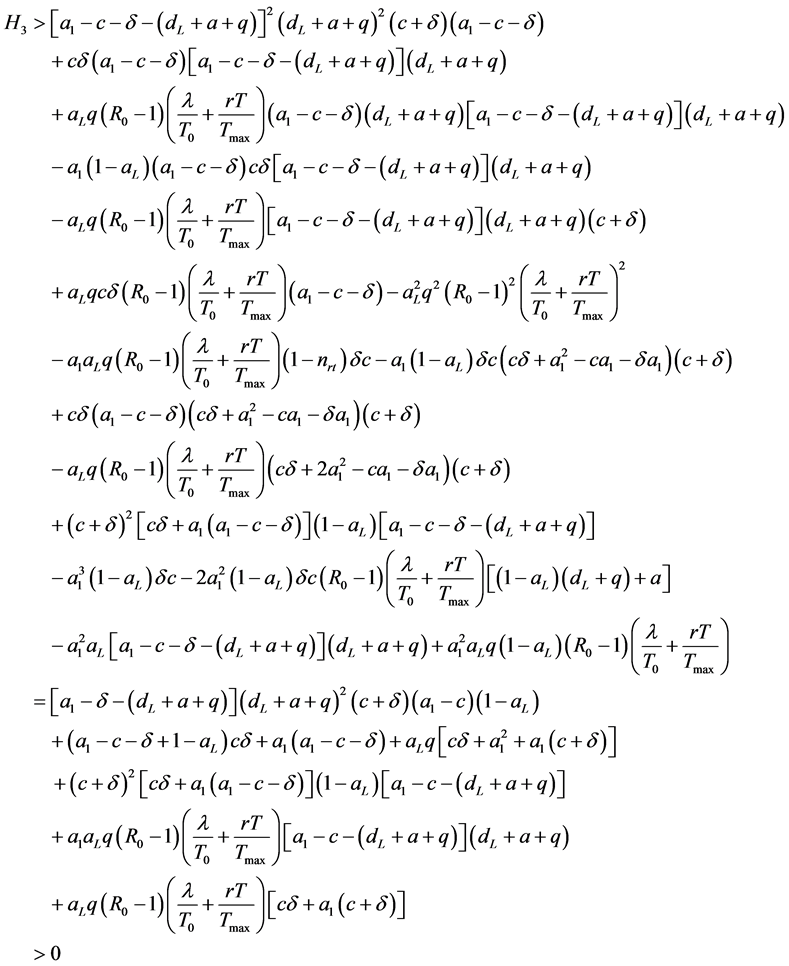
4) 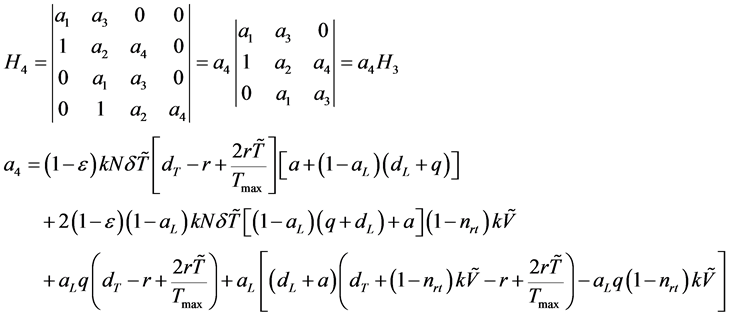
因此,当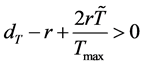 时,
时,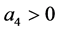 ,即
,即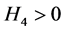 。
。
综上,由Routh-Hurwitz判据可知特征方程的所有根都具有负实部。因此,当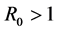 且
且 时,感染平衡点
时,感染平衡点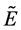 是局部渐近稳定的。
是局部渐近稳定的。
6. 数值模拟
参数表见表1。
6.1. 未感染平衡点的局部渐近稳定性
各参数的数值如表1的数据1,可知基本再生数 ,所以未感染平衡点
,所以未感染平衡点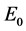 是局部渐近稳定的。选取初值为
是局部渐近稳定的。选取初值为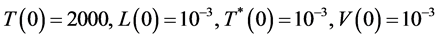 。运用Matlab软件进行编程计算并作图,得出结果见图1。
。运用Matlab软件进行编程计算并作图,得出结果见图1。
从图1可以看出,模型的数值模拟结果趋于未感染平衡点 ,其中,经计算未感染细胞的值为
,其中,经计算未感染细胞的值为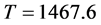 与平衡状态
与平衡状态 相吻合,而潜伏感染细胞L,感染细胞T*,自由病毒V数量都趋于均衡值0。故从数值模拟上未感染平衡点
相吻合,而潜伏感染细胞L,感染细胞T*,自由病毒V数量都趋于均衡值0。故从数值模拟上未感染平衡点 是局部渐近稳定的。
是局部渐近稳定的。

Table 1. The meaning and value of the parameters in the model (2-1)
表1. 模型(2-1)中参数的含义与取值
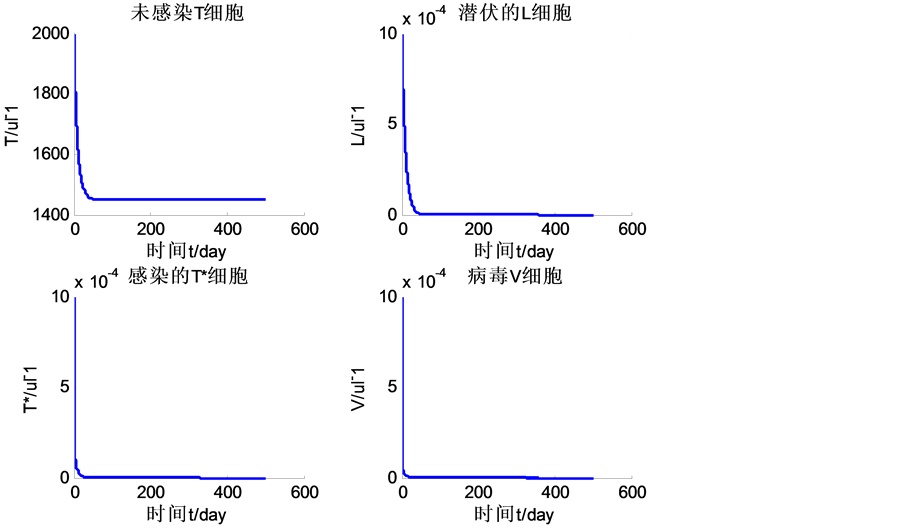
Figure 1. The local asymptotic stability of the uninfected equilibrium point of the model (2-1)
图1. 模型(2-1)的未感染平衡点的局部渐近稳定性
6.2. 感染平衡点的局部渐近稳定性
各参数的数值如表1的数据2,选初值:
 ;
;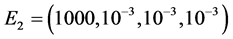 ;
;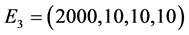 。
。
运用Matlab软件进行编程计算并作图,得出结果见图2。
从图2可以看出,对于不同的初值经过数值模拟得到的四个值最终都趋于定值经过计算得 ,
,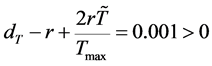 ,通过数值计算得到的数据为
,通过数值计算得到的数据为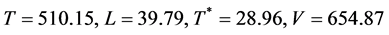 ,与在感染平衡点
,与在感染平衡点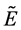 处的数据值
处的数据值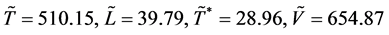 相吻合,因此,从数值模拟上来说感染平衡点
相吻合,因此,从数值模拟上来说感染平衡点 是局部渐近稳定的。
是局部渐近稳定的。
7. 模型比较
7.1. 与非Logistic增长模型比较
当不考虑T细胞的自身增殖的情况下,HIV感染动力学模型为:
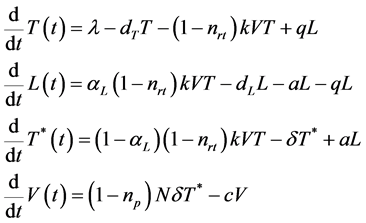 (7-1)
(7-1)
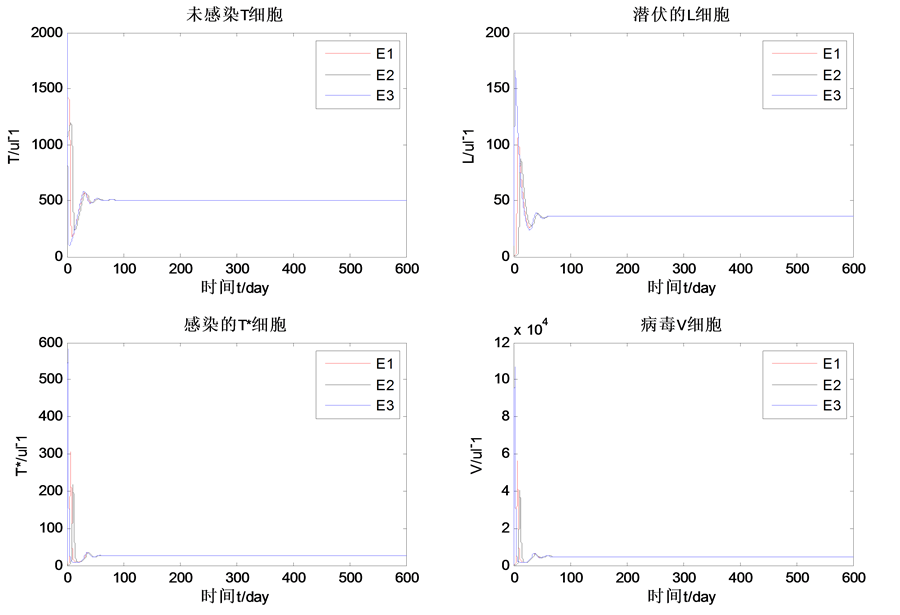
Figure 2. The local asymptotic stability of the infected equilibrium point of the model (2-1)
图2. 模型(2-1)的感染平衡点的局部渐近稳定性
下面通过数值模拟来比较模型(7-1)和含模型(2-1)的区别。各参数的数值参看表1的数据3,选取初值为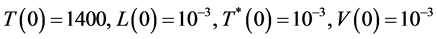 。运用Matlab软件进行编程计算并作图得出结果见图3。
。运用Matlab软件进行编程计算并作图得出结果见图3。
从图3可以看出在T细胞具有Logistic增长的情况下,潜伏感染的T细胞浓度L,受感染的T细胞浓度T*和自由病毒浓度V都明显大于T细胞不具有Logistic增长的情况,即在不考虑T细胞自身增殖的情况下低估了潜伏感染的T细胞、受感染的T细胞和自由病毒的浓度。
7.2. 与非潜伏感染模型比较
当不考虑存在潜伏感染的T细胞的情况时,HIV感染动力学模型为:
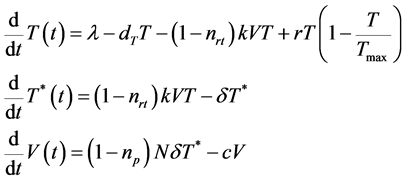 (7-2)
(7-2)
通过数值模拟来比较模型(2-1)和模型(7-2)的区别。各参数的数值仍参看参数表的数据3,选取初值为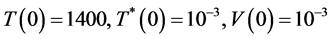 。运用Matlab软件进行编程计算并作图,得出结果见图4。
。运用Matlab软件进行编程计算并作图,得出结果见图4。
由图4可以看出,在具有潜伏感染T细胞的情况下体内T细胞的总量要比非潜伏模型多,而病毒载量基本相同。这说明非潜伏模型低估了人体内T细胞数量,而对病毒载量的影响不是很明显。

Figure 3. The comparison results of model (2-1) and model (7-1)
图3. 模型(7-1)和模型(2-1)的比较结果
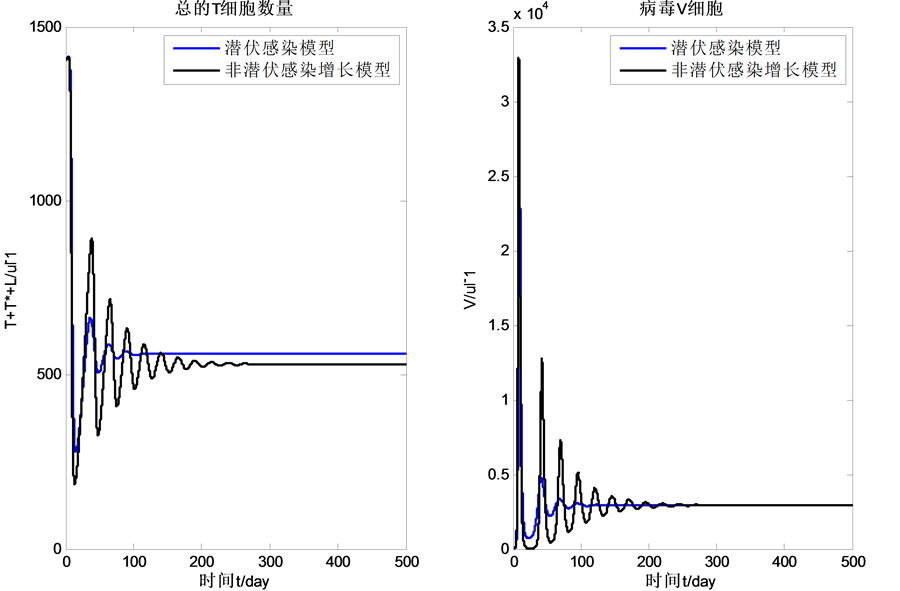
Figure 4. The comparison results of model (2-1) and model (7-2)
图4. 模型(2-1)和模型(7-2)的比较结果
7.3. 与非药物治疗模型比较
当不考虑存在药物治疗的情况时,HIV感染动力学模型为:
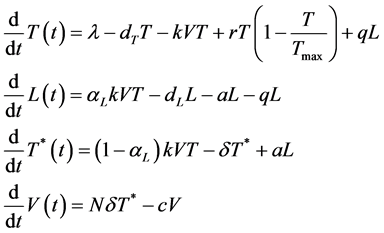 (7-3)
(7-3)
通过数值模拟来比较模型(2-1)和模型(7-3)的区别。各参数的数值参看表1的数据4,选取初值为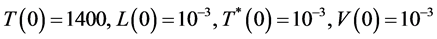 。运用Matlab软件进行编程计算并作图,得出结果见图5。
。运用Matlab软件进行编程计算并作图,得出结果见图5。
由图5可以看出,进行药物治疗时健康的T细胞浓度、感染的T细胞浓度、病毒载量的浓度都明显大于不进行药物治疗时的细胞浓度,而进行药物治疗时潜伏感染的T细胞浓度略大于不进行药物治疗时的细胞浓度,这说明在不考虑药物治疗的情况下低估了T细胞、潜伏感染的T细胞、受感染的T细胞、病毒载量的浓度。
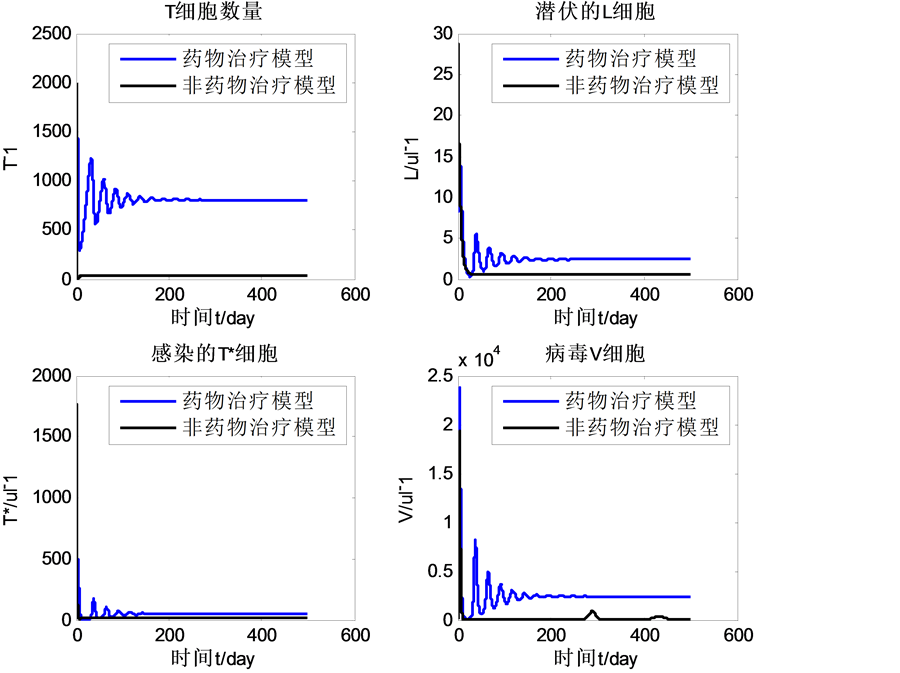
Figure 5. The comparison results of model (2-1) and model (7-3)
图5. 模型(2-1)和模型(7-3)的比较结果
8. 结语
本文在具有潜伏感染的HIV模型中考虑了潜伏感染细胞以一定比率恢复成健康T细胞、T细胞具有Logistic增长以及药物治疗因素。首先求出了模型的两个平衡点,并通过微分方程稳定性理论证明了在基本再生数小于1时是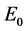 局部渐近稳定的,进一步通过构造Lyapunov函数证明了
局部渐近稳定的,进一步通过构造Lyapunov函数证明了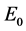 是全局渐近稳定的。
是全局渐近稳定的。
当 时且
时且 时感染平衡点
时感染平衡点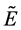 是局部渐近稳定的。接下来根据一些国际权威杂志发表的
是局部渐近稳定的。接下来根据一些国际权威杂志发表的
文献中的数据对模型进行了数值模拟,验证了平衡点的稳定性。最后通过将具有Logistic增长与不具有Logistic增长,具有潜伏感染与不具有潜伏感染,具有药物治疗与不具有药物治疗的模型进行比较来显示HIV的感染过程,揭示其潜伏规律,从而为相关医学工作者提供理论基础与数据依据。
基金项目
中国石油大学(华东)大学生创新创业训练计划资助项目(20151344)。