1. 引言
柴油机是柴油机动力装置最重要的组成部分,是一个复杂的、强非线性的系统,系统内部包含多个子系统,且各子系统间相互耦合并涉及到多个学科理论知识。柴油机的工作状态直接关系到整个动力装置运行的安全性、稳定性和经济性。因此,采用合适的方法对其工作过程进行较为精确的数值模拟非常重要,可以应用于柴油机的设计、优化和故障诊断等多方面,从而达到缩短研发周期,降低成本及市场风险的目的。
近年来,国内外针对柴油机建模的研究很多,其模型多可分为容积法模型和平均值模型。容积法模型将柴油机划分为控制容积和节流部件,通过工质的流动和能量传递将它们串联起来,例如,为预测柴油机稳态和动态性能,采用容积法对RT-flex60C电控柴油机进行建模仿真 [1] ;通过容积法输出图谱,建立主要输入与输出参数间的关系,并将性能参数图谱应用于推进系统动态性能的分析上 [2] 。平均值模型不研究缸内工质热力参数随曲轴转角的循环波动,重在描述柴油机状态参数的循环平均值随时间的变化 [3] [4] 。以上文献的模型都与某些具体型号的柴油机进行了对比试验,证明了其合理性及精确度,但模型在模块化、可重用性、可扩展性和参数化方面相对欠缺,其模型不具有较宽的适用范围。
本文采用面对对象的建模语言Modelica在Dymola平台上建立了柴油机热力系统的陈述式动态模型。Modelica一种基于方程的陈述式多领域统一建模语言,具有面对对象和模块化建模的特点,使系统模块即可以独立建立,又可以快速组装,其建模思想在很大程度上顺应了知识的可累积、可重用和可重构的指导原则 [5] 。Dymola (Dynamic Modeling Language)是一种基于Modelica语言的复杂多领域建模仿真平台。本文首先从原理上分析并给出了柴油机各组成部件的数学模型,在此基础上利用Modelica语言建立各组件的模块化、参数化模型,利用连接机制将各组件模型组装成柴油机热力系统。
2. 柴油机数学模型
本文以某型舰用四冲程柴油机为研究对象,对其内部发生的一系列热功转换过程进行建模分析,并将系统部件分为:进排气阀、喷油管、膨胀气缸、气缸壁、活塞、曲柄连杆系统等。图1所示为其结构和工作原理示意图。
在建模过程中,采用了如下假设:
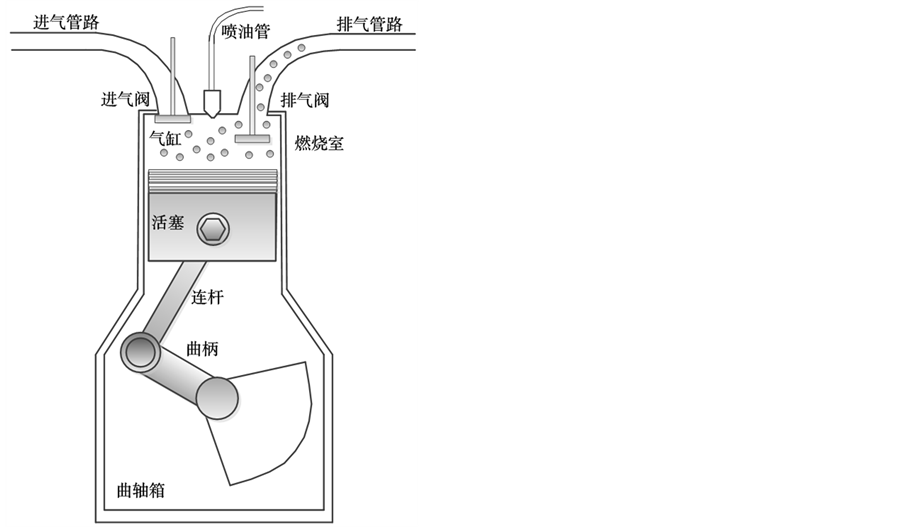
Figure 1. Schematic diagram of working principle of four stroke diesel engine
图1. 四冲程柴油机工作原理示意图
(1) 工质的热力学状态参数仅随时间(曲轴转角)变化,并认为工质在缸内各处的状态是均匀分布的,即处于瞬时热力平衡状态 [6] ;(2) 工质为理想气体,其比热、焓值等参数仅与气体温度和成分有关;(3) 忽略进、排气管内工质的流动过程中所携带的动能,并视为绝热;(4) 喷油燃烧过程遵循双韦伯曲线燃烧放热规律。
2.1. 气缸模型
气缸是柴油机最主要的部件,四冲程柴油机内部进行的过程分别是进气、压缩、膨胀做功和排气,产生的能量再以压力的形式驱动活塞做功。考虑工质在容器内的累积效应,采用容积法进行建模。由质量守恒、能量守恒和理想气体状态方程一起构成缸内工质状态方程组 [7] :
 (1)
(1)
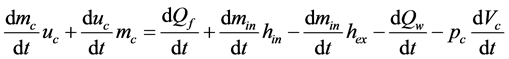 (2)
(2)
 (3)
(3)
式中: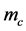 、
、 、
、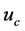 、
、 分别为气缸内工质质量、体积、比内能和气体常数;
分别为气缸内工质质量、体积、比内能和气体常数;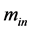 为进气质量;
为进气质量; 为排气质量;
为排气质量;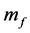 为燃油质量;
为燃油质量; 为燃油放热量;
为燃油放热量; 为进气比焓;
为进气比焓; 为排气比焓;
为排气比焓;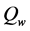 为气缸壁散热量。
为气缸壁散热量。
式(2)中:
 (4)
(4)
式中: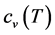 为工质比定容热容(随工质温度变化),
为工质比定容热容(随工质温度变化), 、
、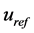 分别为气缸内工质初始参考温度及比内能。
分别为气缸内工质初始参考温度及比内能。
将式(4)代入式(2)中可求得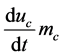 ,故气缸内工质温度为:
,故气缸内工质温度为:
 (5)
(5)
联合求解式(1)~(5),即可确定气缸内工质状态参数随时间的变化规律。
2.2. 进、排气阀模型
进排气阀模块模拟了空气在气缸内的流入和流出的过程,计算了进排气阀前后的压力、流量和空气焓值。气缸内进、排气过程相当于空气流经一个面积随时间变化的孔板,并假定该过程为一维等熵绝热流动,进、排气阀几何开启有效截面积可按以下公式计算 [8] :
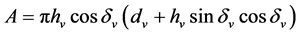 (6)
(6)
式中: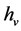 为气门升程,
为气门升程,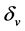 为气阀座锥角,
为气阀座锥角,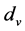 为气阀座喉口直径。
为气阀座喉口直径。
进、排气过程中实际流量与理论流量存在一定差异,这些差异可归结到流量系数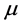 中,可以采用以下经验公式计算:
中,可以采用以下经验公式计算:
 (7)
(7)
2.2.1. 进气阀模型
进气阀前后空气的流动均属于亚声速流动,其进气流量变化率为:
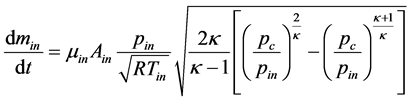 (8)
(8)
式中: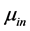 为进气流量系数,
为进气流量系数,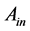 为进气有效截面积,
为进气有效截面积, 、
、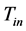 分别进气压力和温度,
分别进气压力和温度,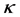 为绝热指数。
为绝热指数。
2.2.2. 排气阀模型
排气可分为两个阶段,初期由于缸内与外界压差较大,可能出现超声速流动,随着压差减小,则转为亚声速流动。
当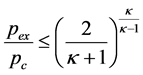 时,为超声速流动,排气流量变化率为:
时,为超声速流动,排气流量变化率为:
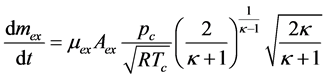 (9)
(9)
当 时,为亚声速流动,排气流量变化率为:
时,为亚声速流动,排气流量变化率为:
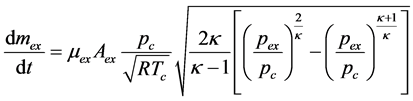 (10)
(10)
式中: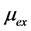 排气流量系数,
排气流量系数,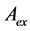 排气有效截面积,
排气有效截面积,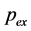 为排气管压力。
为排气管压力。
2.3. 气缸壁散热模型
气缸内燃烧产生的一部分热量通过气缸壁与外界的传热而耗散流失。假定燃烧过程中气缸壁温度恒定,则气缸壁传热量为:
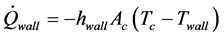 (11)
(11)
式中: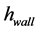 为缸壁传热系数;
为缸壁传热系数;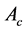 缸壁外表面积;
缸壁外表面积;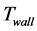 缸壁温度。
缸壁温度。
缸壁传热系数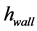 的计算采用Hohenberg教授根据内燃机试验所得的有关数据,经整理得到的如下经验公式 [9] :
的计算采用Hohenberg教授根据内燃机试验所得的有关数据,经整理得到的如下经验公式 [9] :
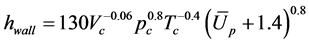 (12)
(12)
式中: 为活塞平均速度。
为活塞平均速度。
2.4. 曲柄连杆系统
曲柄连杆系统的机构如图2所示,根据图中的几何关系可知:
 (13)
(13)
 (14)
(14)
式中: 为活塞速度;
为活塞速度;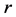 、
、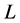 分别为曲柄长度和连杆长度;
分别为曲柄长度和连杆长度;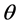 为曲柄转角;
为曲柄转角;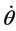 为曲柄转速;
为曲柄转速;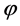 、
、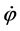 分别为连杆与活塞对称轴形成的角度及其随时间的变化率。
分别为连杆与活塞对称轴形成的角度及其随时间的变化率。
2.5. 活塞
活塞两端分别承受气缸内的压力以及连杆的推力,其所受压力大小为:
 (15)
(15)
式中: 为活塞直径;
为活塞直径; 为活塞所受压力。
为活塞所受压力。
气缸容积大小为:
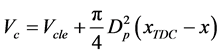 (16)
(16)
式中: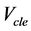 为余隙容积;
为余隙容积;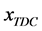 为上止点高度。
为上止点高度。
将式(16)两端对时间进行求导,即可得气缸容积随时间变化规律:
 (17)
(17)
其中: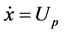 为活塞速度。
为活塞速度。
2.6. 曲柄箱
曲柄箱内的大气压力对活塞的运动有阻力作用,其大小为:
 (18)
(18)
式中, 为大气压力。
为大气压力。
因此,可得连杆作用在活塞上的力的大小为:
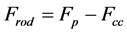 (19)
(19)
2.7. 摩擦损失
参考文献 [6] 通过对多种转速条件下所测得的平均摩擦扭矩值进行线性插值,给出了计算平均摩擦扭矩的经验公式:
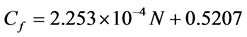 (20)
(20)
式中: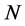 为转速。因此,可知作用在曲轴上的扭矩:
为转速。因此,可知作用在曲轴上的扭矩:
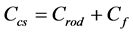 (21)
(21)
2.8. 燃烧放热模型
气缸内燃油燃烧放热规律按下式确定 [10] :
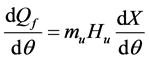 (22)
(22)
式中,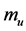 为每缸循环喷油量,
为每缸循环喷油量, 为燃油燃烧低热值,
为燃油燃烧低热值, 为已燃烧燃油质量与每缸循环喷油量之比。
为已燃烧燃油质量与每缸循环喷油量之比。
 与燃烧的物理、化学过程,发动机结构参数、运行状况等诸多因素相关,很难进行精确描述,本文采用双韦伯函数进行半经验公式模拟,将燃烧过程分为预混合燃烧和扩散燃烧两部分,即
与燃烧的物理、化学过程,发动机结构参数、运行状况等诸多因素相关,很难进行精确描述,本文采用双韦伯函数进行半经验公式模拟,将燃烧过程分为预混合燃烧和扩散燃烧两部分,即
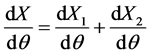 (23)
(23)
式中: 、
、 分别表示预混合和扩散燃烧的燃料分数,并有:
分别表示预混合和扩散燃烧的燃料分数,并有:
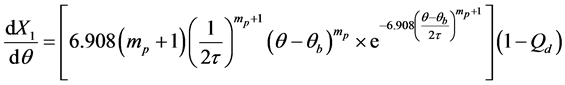 (24)
(24)
 (25)
(25)
式中: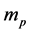 为预混合燃烧品质指数;
为预混合燃烧品质指数;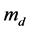 为扩散燃烧品质指数;
为扩散燃烧品质指数;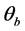 为燃烧始点;
为燃烧始点; 为燃烧终点;
为燃烧终点;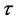 为预混合燃烧领先角;
为预混合燃烧领先角;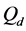 为扩散燃烧燃料分数。
为扩散燃烧燃料分数。
3. 面向对象的冷凝器系统模型的建立
Modelica是面向对象、陈述式的建模仿真语言,可处理大型、复杂多领域的物理问题。陈述式是指模型在描述的过程中不需要人为指定方程的求解顺序,只要系统方程满足封闭条件,即方程数与变量数相同,系统将自动求解计算所有的变量值 [11] 。Modelica采用模块化建模,各部件的数学模型重用性强,减少了大型复杂物理模型的建模难度,部件之间靠接口进行连接,接口中定义了各部件之间进行联系的公用变量。为了实现这一方式,Modelica中定义了如表1所示的八种类:class、package、connector、block、function等。建模过程中,首先根据系统工作原理将研究对象拆分成多个相对简单,贴近物理现实的部件对象,再分别建立各个部件的数学模型并对其数据、特性和结构等进行封装以方便后期进行参数化调用。最后利用Modelica的连接机制,建立整个系统的仿真模型。
3.1. 接口的建立
根据冷凝器系统的特性,建立了几类接口,如用来传递进、排气的质量流量、比焓、温度和压力的接口FlowPort,其在Modelica中的定义如下:
connector FlowPort
Modelica.SIunits.Pressure p;
flow Modelica.SIunits.MassFlowRate m_flow;
Modelica.SIunits.SpecificEnthalpy h;
Modelica.SIunits.Temperature T;
end FlowPort;
Modelica中变量的定义分为势变量和流变量两种,其中势变量表示,流变量是一种“穿过”型变量,表示某种能量流,用关键词flow限定,如FlowPort中的质量流量m_flow。势变量是一种“跨越”型变量,如FlowPort中的压力p、温度T等。
如图3所示,简单来说,势变量和流变量在接口中公式定义有如下区别:
 (26)
(26)
3.2. 组部件的建立
在建立好接口后,根据各部件的具体情况,分别定义接口、变量、参数以及方程式等,即建立各部件的数学模型并最后将模型进行封装。以气缸模型为例,其模型定义如下:

该模型中定义了两个接口,分别用来接收和传递气缸内压力信号和气缸内体积变化速率以及活塞行
程变化速率和活塞作用力。接下来进行参数以及变量的声明,参数声明使用关键词parameter。equation区域用来描述模型的行为。最后对模型进行封装和图形化处理,在之后的建模过程中即可对其进行调用,Dymola平台会根据关键词parameter自动生成该模型的参数列表,在随后的调用过程中对不同型号的部件只需在参数列表上对相应参数进行更改即可,不用反复编写其数字方程。依照相同的方法及流程,分别建立了组成柴油机热力系统的参数化、图形化和模块化部件,如图4所示。
3.3. 柴油机热力系统模型构建
在Dymola平台上建立各部件的模型后,根据柴油机结构及工作原理,利用Modelica中接口的连接机制,将各部件组成连接,建立了柴油机热力系统模型,如图5所示。针对不同型号的柴油机,可对各部件参数进行更改,设定相应的工作环境及工况,实现仿真分析。
4. 仿真结果与分析
本文以某型舰用四冲程柴油机为研究对象,表2所列为该型柴油机的基本参数。
4.1. 模型验证
为验证模型的准确性,根据图5所示的模型及各部件状态方程,利用柴油机推进特性试验提供的进、排气管压力和温度参数作为模型计算的边界条件进行仿真试验,利用Dymola仿真平台分别对柴油机在25%、50%、75%、85%、100%负荷进行了仿真试验,各主要性能参数与实测值的对比情况如表2所示。表中: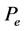 为有效功率;
为有效功率;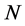 为转速;
为转速;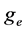 为油耗;
为油耗; 为最大爆发压力;
为最大爆发压力; 为排气温度。
为排气温度。
图6所示为在Dymola平台上计算出的模型在标定工况下缸内压力与曲轴转角的示功图。由表3可

Figure 4. Diesel engine system model base
图4. 柴油机系统模型库
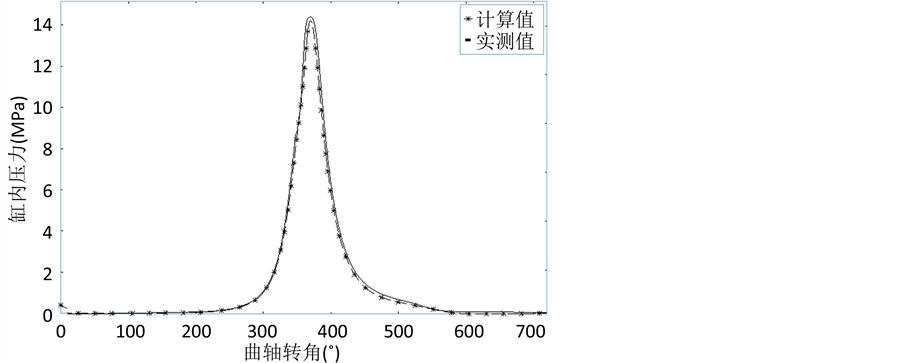
Figure 6. Indicator diagram under calibration conditions
图6. 标定工况下示功图
知,模型计算的柴油机各项主要性能参数与实测数据基本吻合,证明模型具有较高的计算精度,基于该模型对柴油机进行性能分析可信度较强。
4.2. 供油提前角对柴油机主要性能参数的影响
以模型为基础进行仿真研究的目的之一,是利用模型高效、经济、数据完善、模拟精度高的特点,对仿真对象进行性能分析 [12] 。本文分别以供油提前角为例,利用模型进行性能仿真,分析该项参数对柴油机性能的影响。

Table 3. Comparison of simulation and experimental data of engine performance
表3. 多种工况下主要性能参数仿真值与实测值对比
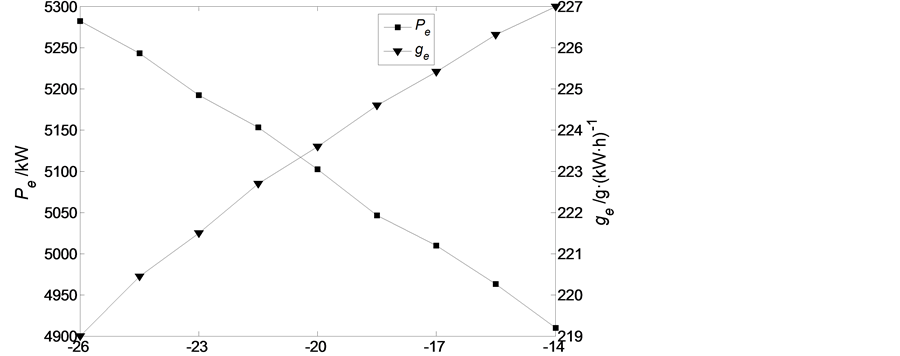
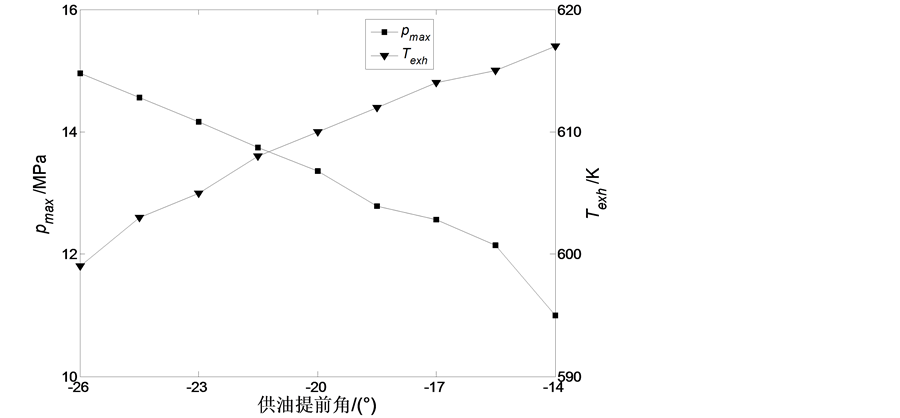
Figure 7. Variation of engine performance parameters with different compression rations
图7. 柴油机性能参数随供油提前角的变化
供油提前角指的是喷油泵柱塞向高压油管开始供油的时刻,关系到整个燃烧过程的完善程度。以活塞在上止点的时刻对应0˚曲轴转角,计算了供油提前角分别为−26˚、−24.5˚、−23˚、−21.5˚、−20˚、−18.5˚、−17˚、−15.5˚和−14˚时的柴油机主要性能参数变化,其它参数保持不变,结果如图7所示。
从图7中可以看出,随着供油提前角的减小,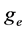 和
和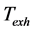 逐渐增大,而
逐渐增大,而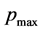 与
与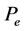 则随之减小。其主要原因为:供油时间推迟使得主要燃烧阶段后移,燃料燃烧不完全,降低了最大爆发压力,增加了耗油量,排气温度也随之增高,从而导致功率下降。例如,当供油提前角为−14˚时,功率比标定工况下降了5.43%。但是,供油提前角过大又会导致柴油机不易启动、工作粗暴等问题。因此,选择好适当的供油提前角后,需要对其进行定期检查、调整。
则随之减小。其主要原因为:供油时间推迟使得主要燃烧阶段后移,燃料燃烧不完全,降低了最大爆发压力,增加了耗油量,排气温度也随之增高,从而导致功率下降。例如,当供油提前角为−14˚时,功率比标定工况下降了5.43%。但是,供油提前角过大又会导致柴油机不易启动、工作粗暴等问题。因此,选择好适当的供油提前角后,需要对其进行定期检查、调整。
5. 结论
本文以某型舰用四冲程柴油机为研究对象,从基本物理规律出发,采用陈述式建模语言Modelica在Dymola平台上实现了模型的建立及运算,并利用实测数据对模型进行了验证,最后分析了压缩比、供油提前角对柴油机标定工况下主要性能参数的影响。仿真结果表明:
(1) 与传统的过程式建模相比,采用Modelica语言建模具有良好的开放性和可扩展性。其图形化、模块化建模过程使系统各部件之间关系清晰明了,模型易于理解,并具有很好的通用性和可扩展性;
(2) 通过与实测数据相比,证明了所建立的柴油机模型具有较高的精度,可用于分析多项参数对柴油机主要性能的影响,从而为柴油机性能分析和优化提供参考,所得结论具有一定理论和工程实用价值。