1. 引言
2007年,美国爆发次贷危机,多家大型的投资银行及其他金融机构相继倒闭,它致使全球主要金融市场出现流动性不足危机,给全球的银行系统和金融系统造成了巨大的冲击,最终引发了一场全球性金融危机。此次金融危机表现出了全球一体化后银行系统的脆弱性和关联性,银行间日趋紧密的联系似乎有助于降低金融危机爆发的可能性,然而一旦发生了,这个危机就会演变成全球性的危机。因此,研究银行系统性风险已成为国内外学术界和政府监管机构关注的焦点。这一研究无疑对防范和化解系统性风险、维护中国金融稳定具有重要意义。
同业拆借业务不仅能够帮助银行调剂流动性,也是商业银行获取较低成本资金的主要方式之一,是利率市场化条件下商业银行应对存款压力、息差收窄压力、拓展经营收益的重要方式之一。但是,由同业拆借业务所构成的复杂的银行间拆借网络是违约传染的主要渠道之一,因此利用网络模型研究银行系统性风险是近期的一个研究热点 [1] 。
2000年,Allen,Gale [2] ,Freixas [3] 等人的研究最早提出:银行间的传染与银行间拆借网络结构有关。此后,学者们对不同国家的银行间拆借网络进行实证研究,发现真实的银行拆借网络与其他领域的网络如国家电网、社区网络等同样具有复杂网络的结构特征。其中,Upper与Worms [4] 在完全市场结构下研究发现德国银行危机传染与金融安全网的存在有很大关系。Boss等 [5] 发现奥地利银行网络具有社团结构和层次结构特征,此外,该银行网络还呈现出小世界结构特征;Iori [6] 等研究发现意大利银行间市场是随机网络;在我国,高国华等 [7] 利用61家银行2009年年报数据对基于资产负债表关联的银行间市场双边传染风险进行研究,从信用违约和流动性风险角度对传染路径和资本损失进行估测,并深入分析银行间市场的不同结构对传染效应的影响。隋聪等人 [8] 通过仿真模拟,研究发现:集中度越高的网络,由于传染而倒闭的银行数量就越多。但是,当基础违约的银行数量不多时,网络集中度(与标度参数负相关)越高,由于传染而倒闭的银行的总资产越少。此外,在集中度高的网络中,大银行倒闭引发违约传染的可能性和影响力都会大于集中度低的网络。而小银行引发传染的可能性远低于大银行,但是当小银行倒闭达到一定规模时,可以引发大银行传染倒闭。
为了探究随机银行网络系统在面对不同强度存款冲击时的稳定性,本文首先基于随机图构建了银行间的随机拆借网络,随后通过描述银行资产负债表结构建立了银行网络动态演变过程,进而应用Garch模型估算模型中动态存款冲击参数及动态投资冲击参数。最后对模型进行了仿真研究,分析了不同存款冲击强度下银行系统的稳定性情况
2. 模型
2.1. 随机银行拆借网络的构建
在银行系统中,为了满足系统中银行对流动性的需求而产生了银行同业拆借市场,流动性盈余银行为流动性短缺银行提供资金借贷,银行间的信贷关系将银行系统构成一个网络。在这个网络中,节点代表各家银行,节点间的连线则代表银行间的债权债务关系。
本文假定系统中所有银行组成的集合为 ,用邻接矩阵
,用邻接矩阵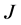 来表示
来表示 包含的银行之间是否存在拆借关系,用债务矩阵
包含的银行之间是否存在拆借关系,用债务矩阵 来表示银行间实际同业拆借额度。
来表示银行间实际同业拆借额度。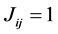 表示银行
表示银行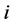 和银行
和银行 之间存在拆借关系,
之间存在拆借关系, 表示
表示 和
和 不存在拆借关系。
不存在拆借关系。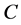 表示银行系统的连接度,
表示银行系统的连接度, 表示系统内不存在银行间的拆借市场,
表示系统内不存在银行间的拆借市场, 表示系统内任意两个银行之间都存在拆借关系,即完全网络结构。
表示系统内任意两个银行之间都存在拆借关系,即完全网络结构。
经典的随机网络 [9] 可定义为:给定 个顶点,任意两个顶点之间都以相同的概率
个顶点,任意两个顶点之间都以相同的概率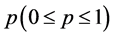 进行连接,整个银行网络的总的连接数在
进行连接,整个银行网络的总的连接数在 左右波动。本文根据此定义来构造随机银行拆借网络,从而确定邻接矩阵
左右波动。本文根据此定义来构造随机银行拆借网络,从而确定邻接矩阵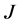 中元素的取值,此处
中元素的取值,此处 。一般来说借贷关系是相互的,因此本模型的邻接矩阵是对称的,
。一般来说借贷关系是相互的,因此本模型的邻接矩阵是对称的, ,即
,即 能借给
能借给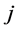 ,
,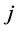 也能借给
也能借给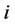 。此外,银行不能与自身发生借贷关系,所以规定
。此外,银行不能与自身发生借贷关系,所以规定 。邻接矩阵
。邻接矩阵 表示如下:
表示如下:

2.2. 银行资产负债表结构及其动态演变模型的构建
表1是本文假设的简易银行资产负债表,涉及的科目都与本模型直接相关。根据表1,可得恒等式(1):
 (1)
(1)
 (2)
(2)
模型包括期初,期中,期末三个阶段 [10] ,如图1。 表示投资期,
表示投资期, 表示第
表示第 家银行,
家银行, 是存款利率,
是存款利率,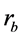 是拆借利率,
是拆借利率,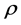 是投资收益率,
是投资收益率,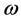 投资机会,
投资机会, 是存款波动,
是存款波动,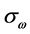 是投资机会波动,
是投资机会波动, 是分红金额,
是分红金额, 是央行规定的存款准备金率,
是央行规定的存款准备金率,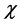 是银行规定的所有者权益占存款比例的下限,
是银行规定的所有者权益占存款比例的下限, 表示系统演化的时间步。下列公式中,
表示系统演化的时间步。下列公式中, 是外生的变量。
是外生的变量。
1) 期初
每期期初,各银行根据公式(3)先计算出从上期末继承下来的流动性资产。
 (3)
(3)
2) 期中
每期期中流动性资产的计算如公式(4)所示,可以分解成以下三个步骤。
第一步:先计算银行在新增(或减少)存款、支付完上期存款利息、收回 期的投资本金及
期的投资本金及 共
共 期投资收益后的流动性资产。
期投资收益后的流动性资产。

Figure 1. Flowchart of dynamic banking system
图1. 银行系统动态演变模型流程图
第二步:计算上期的拆入拆出净额,当拆借净额(拆出减去拆入)小于0并且该绝对值大于第一个步骤计算的流动性资产时,该银行因无法偿还上期同业负债直接破产并进行清算。
第三步:对上期的拆借利息进行核算。公式(5)是存款的随机波动模型,每一期的存款均与上一期相关,且存款冲击 是随时间变化的一个动态值,式中
是随时间变化的一个动态值,式中 是存款冲击系数,默认值为1,进行模型仿真时通过改变 来控制存款冲击强度。
是存款冲击系数,默认值为1,进行模型仿真时通过改变 来控制存款冲击强度。
通过以上三个步骤更新流动性资产后,银行节点的状态也会被更新,按照流动性状态分为四种:流动性盈余的银行是流动性资产大于准备金的银行,即潜在贷方;流动性不足的银行是流动性资产小于零且有潜在借方的银行,即潜在借方;流动性资产小于零且无潜在贷方的是违约银行;普通银行(即非上述三种)。在后面章节的仿真计算中,每一次流动性资产的变化都会伴随着银行节点状态的更新。
 (4)
(4)
 (5)
(5)
 (6)
(6)
3) 期末
流动性盈余的银行会在期末进行分红和投资。公式(8)表示了t期的分红金额,首先在银行利润、减去存款准备金后的流动性资产、可支配的资本中取最小值,其次要满足分红金额不小于零的条件。银行在每期都会面临一些投资机会,假设这些投资机会是随机的,服从正态分布,如公式(10)所示。投资必须同时满足投资机会和已有流动性的约束,即实际的投资额不能超过投资机会大小,同时,当银行现有流动性资金为正时,则将不大于投资机会的所有流动性资金用于投资,否则只能放弃投资机会,如公式(9)所示。
 (7)
(7)
 (8)
(8)
 (9)
(9)
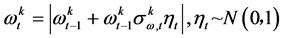 (10)
(10)
 (11)
(11)
2.3. 应用Garch模型估算动态冲击参数
在一个时间序列中,如果有的时候波动性很大,而有的时候波动性却很小,也就是说波动性既有爆发性又有积聚性,这时称该时间序列存在条件异方差。Garch类模型特别适合于对金融时间序列数据的波动性和相关性进行建模,估计或预测波动性和相关性。
动态冲击强度下的银行系统模型中的动态冲击指动态存款冲击和动态投资冲击。该模型中应用Garch模型估测 银行
银行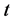 时刻的存款冲击
时刻的存款冲击 和投资冲击
和投资冲击 。本文采用形式最简单也是实际中最常用的GARCH(1,1)模型,即它只有一个自回归项和一个滞后的扰动项。估计存款冲击的条件方差方程为:
。本文采用形式最简单也是实际中最常用的GARCH(1,1)模型,即它只有一个自回归项和一个滞后的扰动项。估计存款冲击的条件方差方程为:
 (12)
(12)
条件均值方程为:
 (13)
(13)
其中, 为回归系数,
为回归系数, 为滞后系数,
为滞后系数, 均为待估参数。估计投资冲击的条件方差方程为:
均为待估参数。估计投资冲击的条件方差方程为:
 (14)
(14)
条件均值方程为:
 (15)
(15)
3. 数据选取与参数估算
3.1. 数据选取
本节对MATLAB的仿真环境进行设置。假设该随机银行网络中银行的节点数为400,时间步 ,
, 为银行系统的演化时间。我们根据16家银行的分支机构现状,按照分支机构的比例,将400家银行按照银行的规模划分为16类银行,每一类银行的数量及相关初始值如表2。
为银行系统的演化时间。我们根据16家银行的分支机构现状,按照分支机构的比例,将400家银行按照银行的规模划分为16类银行,每一类银行的数量及相关初始值如表2。
从银行2015年年报中获取存款初始值 和投资机会初始值
和投资机会初始值 (以2015年的投资额作为投资机会的初始值),参照表3。假设投资期
(以2015年的投资额作为投资机会的初始值),参照表3。假设投资期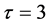 ,资产比率
,资产比率 ,该值限定了银行资本储蓄比只有高于30%时才能分红,从而确保只有盈利才能分红。存款准备金率
,该值限定了银行资本储蓄比只有高于30%时才能分红,从而确保只有盈利才能分红。存款准备金率 ,活期存款利率为
,活期存款利率为 ,投资收益率
,投资收益率 ,同业拆借利率
,同业拆借利率 ,介于存款利率和投资收益率之间。
,介于存款利率和投资收益率之间。

Table 2. The number of different type of bank
表2. 各类银行数量

Table 3. Initial amount of deposits and investment opportunity
表3. 银行的初始存款规模以及初始投资机会
3.2. 动态冲击参数估计
本节搜集了我国16家上市股份制银行从2000年至2015年各季度的资产负债表信息、利润表信息及现金流量表信息,数据来源于同花顺。首先,根据已有的历史数据,估算了存款冲击的条件方差方程(公式12)中的待估参数 ,然后利用这些参数预测下一阶段的存款冲击,作为模型中存款冲击的初始值
,然后利用这些参数预测下一阶段的存款冲击,作为模型中存款冲击的初始值 。相关结果见表4。
。相关结果见表4。
用相同的方法可以估算出投资冲击的条件方差方程(公式14)中的待估参数 ,然后利用这些参数预测下一阶段的投资冲击,作为模型中投资冲击的初始值
,然后利用这些参数预测下一阶段的投资冲击,作为模型中投资冲击的初始值 。相关结果见表5。
。相关结果见表5。
4. 仿真研究
4.1. 存款冲击系数与连接度对稳定性的影响
基于动态存款冲击的波动公式(8),通过改变冲击系数 来模拟不同存款冲击强度下,银行系统在不同连接度在的稳定性。
图2显示,随着冲击强度的增大(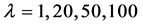 ),银行系统变得不稳定。这与市场的实际情况相符合,当存款冲击增大,银行的流动性资产的波动增大,银行发生违约的概率增加。此外,对以上四种不
),银行系统变得不稳定。这与市场的实际情况相符合,当存款冲击增大,银行的流动性资产的波动增大,银行发生违约的概率增加。此外,对以上四种不

Table 4. The predicted values of deposit shock
表4. 预测存款冲击相关参数估计结果

Table 5. The predicted values of investment shock
表5. 预测投资冲击相关参数估计结果

Figure 2. Flowchart of dynamic banking system
图2. 银行系统动态演变模型流程图
同强度的冲击而言,都有如下结论:当 时,增大冲击对系统造成的不稳定程度远大于
时,增大冲击对系统造成的不稳定程度远大于 的系统内受到的不稳定影响。这意味着,银行之间的连接可以提高系统面临存款冲击时的稳健性。如表6所示,
的系统内受到的不稳定影响。这意味着,银行之间的连接可以提高系统面临存款冲击时的稳健性。如表6所示, 时违约银行的变化数量远大于其他
时违约银行的变化数量远大于其他 的情况。
的情况。
4.2. 探究随机网络下的最优连接度
4.1节的仿真结果显示了连接度与银行稳定性之间不是单调的线性关系。图2中 的曲线与
的曲线与 的曲线越来越接近,当
的曲线越来越接近,当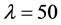 时两条线基本重合,并且当
时两条线基本重合,并且当 时,
时,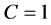 的曲线反而在
的曲线反而在 的下方。说明,随着存款冲击的增大,完全连接的市场稳定性逐渐变差,不再是最优银行连接度。因此,本节我们探究在更多不同连接度下,随着冲击强度的增大(
的下方。说明,随着存款冲击的增大,完全连接的市场稳定性逐渐变差,不再是最优银行连接度。因此,本节我们探究在更多不同连接度下,随着冲击强度的增大( ),银行系统稳定性变化。经过仿真,可以得到随机网络下,面临不同的冲击时最优连接度范围不同,总体来说,最优连接度的范围在
),银行系统稳定性变化。经过仿真,可以得到随机网络下,面临不同的冲击时最优连接度范围不同,总体来说,最优连接度的范围在 ,如图3。
,如图3。
4.3. 连接度对初次违约时间的影响
当连接度在最优范围的情况下,连接度C的大小对银行系统稳定性影响不太明显,但是对于第一次违约发生的时间有比较明显的影响。在最优连接度 的范围内,是遵循着连接度越大,第一次违约越晚发生的规律,如图4。
的范围内,是遵循着连接度越大,第一次违约越晚发生的规律,如图4。
表7表明,连接度越大的银行系统越容易发生银行倒闭的“雪崩现象”,在大于最优连接度范围的系统里,当面临存款冲击的时候,虽然第一次发生银行倒闭的时间晚,但是系统内银行会在短时间内大量违约,最终系统内未违约银行数更少,因此长远来看,银行之间过度的连接不利于银行系统的稳定性。

Table 6. The amount of defaults related to connectivity and deposits shocks
表6. 不同条件下违约银行数量

Figure 3. The amount of defaults related to connectivity and deposits shocks
图3. 不同条件下违约银行数量
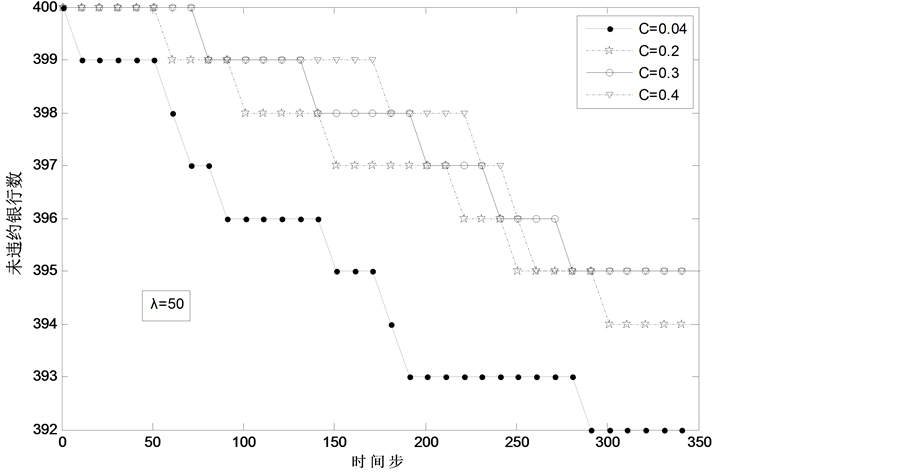
Figure 4. The relation between time step and the amount of non-defaulting banks ( )
)
图4. 存款冲击系数 时系统内未违约银行数量
时系统内未违约银行数量
5. 结语
本文对随机银行网络系统的稳定性进行了研究,探究其在面临不同强度的存款冲击、不同连接度时的系统稳定性。系统中的研究对象为异质性银行(即存款规模和投资机会各不相同),首先基于随机图构建了动态冲击强度下随机银行网络系统模型,设置了模型中基本参数的取值,其中包括用Garch模型基于银行历史数据估算各银行动态的存款波动和投资机会波动。进而进行仿真模拟,结果表明:1) 存款冲击强度越大,银行系统越不稳定,银行之间的连接可以提高系统面临存款冲击时的稳健性;2) 银行网络系统在面临存款冲击时,存在最优连接度,且不同强度的存款冲击条件下,其最优连接度不同;3) 在最优

Table 7. The time of first default occurred in different connectivity
表7. 不同连接度下银行首次违约的时间
连接度范围内,连接度越大,第一次倒闭越晚发生;此外,连接度越大的银行系统越容易发生银行倒闭的“雪崩现象”,因此长远来看,银行之间过度的连接不利于银行系统的稳定性。