1. 引言
Apriori算法是数据挖掘中关联规则产生的一种经典算法，其过程为找出数据库中相关联的频繁项集，然后根据频繁项集产生的强关联规则，根据实际应用设定阈值，筛选出最终结果 [1] 。实践表明，Apriori算法处理大数据时存在大量I/O操作和CPU的开销，使得运算效率出现瓶颈，这制约了其在数据挖掘中的应用性 [2] 。本文对Apriori算法进行改进，使其适用于入侵检测系统中，同时克服存在的问题。分析改进后性能，使其具有良好有效性。
2. 传统Apriori算法
Apriori算法是关联规则挖掘频繁项集算法，其核心思想是通过两个阶段挖掘频繁项集，分别是生成候选集以及封闭的向下检测。挖掘步骤总体上分为两个部分，首先根据支持度生成所有频繁项集，然后在此基础上根据置信度生成关联规则 [3] 。
2.1. Apriori传统算法步骤
Apriori算法挖掘步骤如下：Apriori算法采用迭代方法进行逐层搜索，搜索“1-K项目集”。首先，找到“频繁1项集”，这是表示为L1的集合。L1被用来寻找“频繁2项集”L2，再通过L2找到L3。以此类推，直到没有找到的“K项集”。每次找到Lk都需要扫描一次原始数据。其核心思想是：连接过程和剪枝过程。连接过程使用自连接，通过字母顺序连接并确保前K-2项相同。修剪过程是让任何频繁项集的所有非空子集也必须是频繁。反之，如果一个非空子集不是频繁集，那么候选集肯定是不频繁，所以可以从CK删除它 [4] 。
具体步骤如下：
1) 产生每个频繁集L的所有非空集；
2) 对于每个非空集合L的S，如果P(L)/P(S) ≥ min_conf，则输出规则S→L-S图1为一个执行Apriori算法的过程，最小支持度为2。
第一步骤中该算法的第一次迭代后，事务数据库将进行扫描，计算出包含在D中的每个项目的数目以生成一组候选1项集C1。
第二步骤中，根据所述最小支持度的设置在C1的基础上来确定频繁1项集L1。
第三步候选2项集C2由L1生成，然后对C2包含的数据项集进行扫描计数。
第四步，根据最小支持度的设置，从候选集C2中生成频繁集L2。
第五步是由频繁2项集L2生成候选3项集C3，设置生成候选3项集的C3 = {{1,2,3}，{1,3,5}，{2,3,5}}，根据Apriori修剪的性质：所有的频繁项目集的任意自己都是频繁项目集，{1,2,3}的一个子集{1,2}，不包含在频繁2-项集L2中，因此{1,2,3}被删除。项集{1,3,5}的{1,5}也不包含在L2中，所以删除{1,3,5}，而{2,3,5}项目集所有自己均为L2的元素，它被保留下来(图1)。
3. Apriori在入侵检测中的改进
传统的Apriori算法通过迭代的方法生成候选集。一些人通过减少候选项集,减少扫描时间改善算法效率。但是Apriori算法的性能瓶颈主要原因是自连接操作的所需要的迭代 [5] 。本文使用了一种基于非迭代的改进Apriori算法，主要应用于IDS告警日志分析。由于在IDS检测中较少的属性所产生的关联规则往往没有价值，更有价值的是那些通过多维属性得到的关联规则。
3.1. Apriori算法改进及计算步骤
改进后的Apriori算法步骤如下：定义一个函数count(X)，以此表示要获得项集X需要进行交集运算的次数。令X的支持度为n，如果有任何两个项目之间有交集，交集的总数为count(x)。s(X)与count(X)之间的关系应为：
。
综上所述，我们可以由项集的count计数函数得到它的支持度而不用每次重新扫描一次数据集。
算法总体分为如下几步：
第一步是转化阶段，为诸如协议类型，警报类型，以及攻击类别建立索引，以便简化交集操作 [6] 。
第二步是集合相交阶段，在交易之间做交集，以获得最大项集。如果结果被发现在候选项集的列表中，该计数器+1，否则，结果被插入到列表，计数器被重置为1，计数器表示用于该事务的支持度。
Figure 1. Apriori algorithm example
图1. Apriori算法实例
第三步是获得所有的频繁项集。在列表中的计数器被转换成支持度的值并通过比较找出最低支持度以上的项集，则其为频繁项集。
第四步为生成关联规则。在我们的系统中，关联规则只涉及攻击类，算法只生成形如X→Y的规则，其中Y是攻击行为。如果一个关联规则的置信度大于或等于min_conf，则为强关联规则。
3.2. Apriori算法改进后计算实例
本文通过一个实例来说明改进的Apriori算法的性能优势。若有数据集合如表1所示。
TID为事务id，Items为项集，ItemsC为在计算交集时需要进行比较的项集，Count为项集支持的数量，Lenth为最大交集元素个数，Flag为标志位,标识该项集是否被删除。算法的具体步骤如下：输入为事务数据集合D以及最小支持数min_sup，设置为4，输出为最大频繁项集MFS (MaxFrequentSet)，记为L首先对整个数据集合进行扫描，
for(each i,j i
if(item j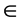 
TID i)
convert(item j); //对上文所述的三个告警日志中的属性进行转换
}
然后为每个item建立一个列表DList，列表中存储包念了该Item的事务ID，即TID，DList与itemList如表2所示。
根据表3可以首先计算出非频繁1-项集{4,5,6,7,8}，然后进行第二次扫描数据库，根据il[]，i2[]，i3[]的数据，求T1与其他事务T2，T3，T5，T6，T8，T9，T10的交集得到频繁项集Fl = {i2,i3}，支持数量为6，因此将i2，i3加入频繁项集FS，并且由于T6与T10中去除了NFS中的项后仅剩余一项，因此直接将其从数据集合中删除，然后更新DList如表4。
由于SC = 1 + 1 + 1 = 3，算法继续，接着求T2中的项的最大频繁项集，因为T2与T1产生了最大频繁项集F1，只需比较T1比较的项即可，同理可知计算T3，T5，T8，T9时也仅需与T1比较的项进行交集，同时F1是在比较的过程中不断更新的，T2比较完后F1仍为{i2,i3}，略去这一步骤，在进行第三次扫描时，T3比较完后F1更新为{i1,i2,i3}，项集支持数量为4，然后在FS中加入新的最大频繁项集{il,i2,i3}:4，然后更新Dlist如表5。
Table 5. Second Updated Dlist
表5. 第二次更新后的Dlist
此时SC = SC + T4.count + T5.count + T7.count + T8.count + T9.count = 10 > 10 − 4 = 6，因此算法结束，在FS中找出最大频繁项集为{il,i2,i3}，支持数量为4，支持度为40%。对比该实例的算法与经典的Apriori算法实现，显然可以看出改进的算法只扫描了3次数据集合，并且第2，3次都只扫描了数据集合的一部分，因此效率显著提高。
4. 结束语
本文基于IDS检测中较少的属性所产生的关联规则往往没有价值该原则，使用了一种基于非迭代的改进Apriori算法，对传统算法存在的额I/O负载大，产生过多的候选项目集等缺点进行改进，极大提高效率，减少对数据库的访问量。改进后的算法实现通过多维属性得到关联规则适用于IDS告警日志分析。为了应对大数据的分布式计算，需要对该算法进行进一步的改进，使其可以很好的适应大数据环境下的分布式入侵检测问题，在海量数据中快速而准确的找出入侵源头，维护系统安全，使其更加适用于分布式计算平台诸如Hadoop中的Map、Reduce等的计算过程。