1. 引言
汽车零部件入厂物流具有高度复杂性和专业性,优化的汽车零部件入厂物流可以降低物流成本且同时提高响应市场的速度和生产柔性,因此它是汽车制造企业增强供应链竞争能力的重要环节。在汽车供应链拉动式结构、零部件采购全球化、整车生产准时化的背景下汽车生产物料供给逐渐形成了递阶供应的模式。汽车零部件一般经过三/四阶递阶供应从供应商到达生产线终端,如图1所示。第一阶集货物流,为零部件从海外供应商经Milk-run循环取料运至海外的集货中心;第二阶取货物流,为零部件从海外集货中心经干线运输运至到国内配送中心,或者为零部件从国内供应商经Milk-run循环取料运至国内的配送中心;第三阶配送物流,为零部件从国内配送中心经配送运输运至国内主机厂货架;第四阶厂内物流,为零部件从主机厂货架经厂内运输运至国内汽车装配线。在这个过程中,第一阶集货物流与第二阶取货物流中都存在着Milk-run循环取料问题,因而Milk-run是汽车零部件入厂物流合理化的重要途径之一,它不仅能够解决由供应商单独配送带来的时间和运输成本问题,并且还能够大幅度提高汽车零部件入厂物流的效率。
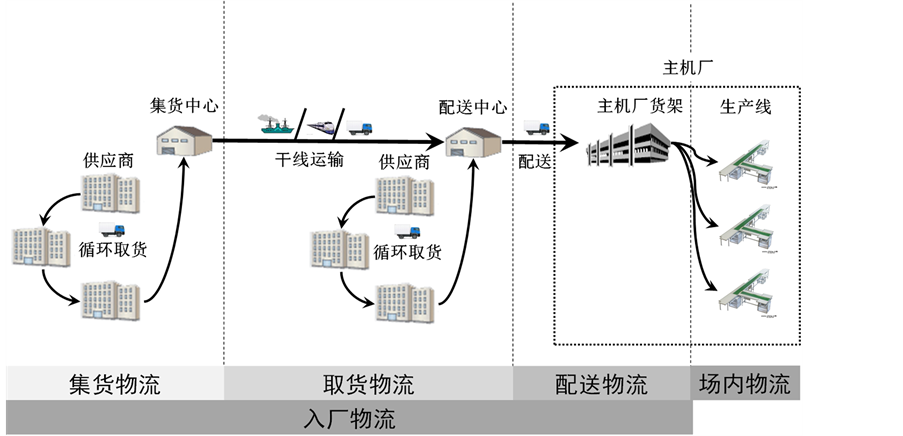
Figure 1. The automobile parts inbound supply chain
图1. 汽车零部件递阶供应示意图
Milk-Run的概念源自奶制品行业,又称循环取货、牛奶式取货等,它的运作方式是车辆从配送中心出发,按照既定的路线和时间要求依次到不同的供应商处收取原料或者零配件,并将其集中到配送中心然后再进行拼装配送到主机厂。Milk-Run的显著优点是能够满足小批量多频次的取货需求并且能够提高车辆的装载率和使用效率,有效减少装配工厂的拥挤、大幅度减少车辆总行驶距离、汽车尾气的排放等。Browersox等人 [1] 指出milk-run取货模式是精益物流战略的重要组成部分。Du等人 [2] 研究了一个集货milk-run取货中心的实时车辆调度系统,并对初始参数进行了分析。文献 [3] [4] [5] 指出milk-run取货模式能够大幅度减少运输距离和物流成本,提高车辆运输效率与减少二氧化碳排放,减少车辆使用量进而改善城市交通状况。但在他们的研究中没有进行针对汽车零部件入厂中milk-run取货模式特征的分析。
汽车零部件中循环取货模式应用的关键是在相关约束条件下的取货路径优化。在汽车零部件入厂物流的实际运作中,处于供应链的核心地位的汽车主机厂奉行JIS、JIT等拉动式生产方式,力求降低自身库存水平,因此对所需零部件到达主机厂的时间做严格的要求。与此同时,为了提升运输环节的车辆利用率,一个供应商的货物可以由多个批次的车辆进行载运,这些情景与传统循环取货模式有一定区别。因此本文针对循环取货在汽车零部件入厂物流中的应用,提出一种新的适应汽车零部件入厂物流中Milk-run循环取料问题特点的混合整数规划模型,并对模型进行分析。同时,本文提出一种启发式算法对该问题进行求解,并通过算法分析和数值实验论证了本文提出的方法可以有效地解决该问题。本文结构如下:第二节对Milk-run循环取料问题与传统车辆路径问题(VRP问题)进行比较分析,提出Milk-run循环取料问题的新特点。第三节本文针对Milk-run循环取料问题构建了混合整数规划模型。第四节针对Milk-run循环取料问题提出一种启发式方法进行求解。第五节通过计算实验分析论证了本文方法的有效性。第六节对全文进行总结。
2. 问题描述
车辆路径问题最早在1959年由Dantzig和Ramser提出,用来描述对天然气服务站的配送。1964年,Clark和Wright提出了一种有效的贪婪算法,提升了Dantzig和Ramser对该问题的求解效率,在这之后的50多年中,大量的研究工作对车辆路径问题进行了研究。汽车零部件入厂Milk-run循环取料问题与车辆路径问题有很大的相似之处。本节将对汽车零部件入厂Milk-run循环取料问题与车辆路径问题之间的异同进行比较分析。
汽车零部件入厂Milk-run循环取料问题是在满足约束条件的情况下找到总运输成本尽量少的路线方案,其应当满足的约束条件如下:(1) 所有车辆都从配送中心出发最终回到配送中心;(2) 每一个供应商的需求取货量可以被一辆或者多辆车取回;(3) 每一个供应商的需求取货量都存在一个卸货要求时间窗;(4) 每一辆车的总取货量都不能超过其对应车型的载货能力。
与汽车零部件入厂Milk-run循环取料问题类似的车辆路径问题主要有:带时间窗的车辆路径问题、需求可拆分的车辆路径问题、多车型车辆路径问题。带时间窗的车辆路径问题由Savelsbergh [6] 最早证明是一个NP-complete问题。之后的研究中,Golden [7] ,Solomon [8] 主要集中于对VRPTW问题可应用求解方法的研究,近年,Raul Banos等人 [9] 提出了一种针对多目标VRPTW问题的混合现代启发式算法,得到优化解决方案。但在这些研究中,并未考虑到卸货时间窗和需求可拆分的特点。需求可拆分的车辆路径问题由Dror和Trudeau [10] 提出,之后Archetti等人 [11] 对应用规模的这一问题进行了启发式方法的研究,国内方面,孟凡超 [12] 、熊浩 [13] 建立了需求可拆分车辆路径问题的数学模型,并设计禁忌搜索算法求解,但这些研究中并未考虑到卸货时间窗的特点。因此汽车零部件入厂Milk-run循环取料问题可以看作是一种新的车辆路径问题的推广,汽车零部件入厂Milk-run循环取料问题是一个NP-hard问题。
3. 问题定义与模型
3.1. 定义
3.1.1. 集合
本文的研究的汽车零部件入厂物流循环取货问题可以被定义在一个全连通图 中,集合定义如下:
中,集合定义如下:
3.1.2. 参数
在以上集合定义的基础上,本模型相关参数定义如下:
3.2.3. 变量
基于以上定义,本模型引入三个变量,分别用来对路径、访问时间和去货量进行决策:
3.2. 模型
本问题所构建目标模型的目标函数及约束条件可以表述如下:
3.3. 模型描述
式(1)为目标函数,表示总成本,即总运输里程成本。式(2)~式(12)为约束条件,其中式(2)表示每个供应商至少被一辆车访问一次;式(3)、式(5)表示所有车辆都由RDC出发,最终回到RDC;式(4)表示访问某个供应商的车辆都一定会离开该供应商;式(6)表示车辆运行的时间顺序,用来避免闭回路的出现;式(7)表示访问供应商的车辆需要满足该供应商的卸货时间窗;式(8)、式(9)表示任意供应商的供货量只能被拆分到经过该供应商的车辆上,且该供应商的供应量需要被完全运载;式(10)表示车辆的总装载量应满足该线路对应车辆的装载能力约束。
4. 算法设计
4.1. 算法框架
上述模型基于现实汽车零配件入厂物流的情景,在传统车辆路径问题(vehicle routing problem)基础上进行延伸,引入需求可拆分以及卸货时间窗等要素,属于NP-Hard问题,难以在合适的时间内得到精确解,因此本文设计改进的启发式算法进行求解,初始解的构造将采用改进的最佳插入法,并运用禁忌搜索算法进一步优化。
4.2. 初始解生成
禁忌搜索算法多初始解依赖性较强,本文将本文采用改进的最优插入算法进行初始解的生成。具体流程如下:
Step 1:集合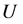 为未访问点的集合,判断
为未访问点的集合,判断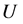 是否为空集,若是则终止;否则转Step 2。
是否为空集,若是则终止;否则转Step 2。
Step 2: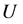 中未访问点按照其距离RDC的距离从大到小进行排序,排序列表为
中未访问点按照其距离RDC的距离从大到小进行排序,排序列表为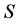 。
。
Step 3:选择 排序中第一个供应商节点来建立一条由RDC出发经过该供应商节点并返回RDC的初始路径。
排序中第一个供应商节点来建立一条由RDC出发经过该供应商节点并返回RDC的初始路径。
Step 4:考察此时路径的总容量是否满载,否则将此供应商阶段从集合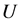 以及列表
以及列表 中删除,并进行Step 6,是则转入Step 7。
中删除,并进行Step 6,是则转入Step 7。
Step 5:考察此时路径是否超载,是否超载,否则该路径构建结束,将最后插入路径的供应商从集合 以及列表
以及列表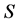 中删除,是则将该店进行拆分,满足路径满载,构建结束,超出部分保留在
中删除,是则将该店进行拆分,满足路径满载,构建结束,超出部分保留在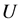 中,转Step 1。
中,转Step 1。
Step 6:对 中任意节点
中任意节点 分别考察其插入现有路径中任意两点
分别考察其插入现有路径中任意两点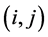 之间时是否满足时间窗约束,将满足条件的节点及其对应位置设为集合。
之间时是否满足时间窗约束,将满足条件的节点及其对应位置设为集合。
Step 7:对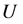 中任一节点
中任一节点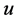 分别计算将其插入现有路径中任意时间窗可行位置
分别计算将其插入现有路径中任意时间窗可行位置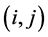 之间造成的成本增加值
之间造成的成本增加值 ,选择具有最小增加值的
,选择具有最小增加值的 的位置
的位置 作为该节点的最佳插入位置,对
作为该节点的最佳插入位置,对 中所有点的最佳插入位置进行比并选取出具有最小成本增加值的节点
中所有点的最佳插入位置进行比并选取出具有最小成本增加值的节点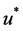 ,将其插入到最佳位置即路径
,将其插入到最佳位置即路径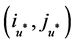 ,转Step 4。
,转Step 4。
4.3. 禁忌搜索算法设计
禁忌搜索算法最早是由美国的Glover提出,它是对局部邻域搜索的一种改进,引入禁忌表,通过该方法来避免因重复搜索而陷入局部最优。每当达到一个局部最优点,就利用禁忌表将该点记录下来,在下一次邻域搜索中,可以有意识的回避这些禁忌表中的局部最优点。因其具有这种禁忌特性,所以相较于局部邻域搜索算法,禁忌搜索算法更易于寻得全局最优。
在禁忌搜索算法的设计过程中,主要的环节包括以下几点:解的表示、解的评价、邻域的构造、禁忌对象及禁忌长度的确定、特赦规则的确定和终止规则的确定。
4.3.1. 解的表示
本实验的解采用需求带与需求量对应分别排列的方式进行表示,用代表RDC,代表各个供应商节点,对应路线用同样顺序构建通过各供应商时的取货量。例如,路径0-3-4-1-0及其对应装载0-1-1-2-0 表明该路线途经3、4、1供应商节点,并依次获取1、1、2单位货物。
4.3.2. 解的评价
本实验以目标函数作为解的评价函数,目标函数的值越小,代表解得质量越高。
4.3.3. 邻域构造
VRP问题的邻域搜索主要有两种,一个是线路内的搜索,另一个是线路间的搜索。本文采用or-opt交换法以及λ-interchange法进行邻域搜索,具体方法如下:
1) or-opt交换法用于线路内的搜索。即在一条路径上选取一点𝑖,寻找其在该路线的最优位置并进行插入操作,且要满足时间窗等约束。由于该操作仅仅是改变了该路径上各点的访问顺序,而总体供货需求量没有改变,因此对该路径而言,容量限制总是可以被保证的,也就不会出现新的拆分或者合并拆分的现象。
2) λ-interchange法用于线路间的搜索,具体又可分为1-0节点交换法、1-1节点交换法和1-2节点交换法。1-0节点交换法是指将某一供应商点从其当前所在的路线中删除,然后将其插入到另一条路径中;1-1节点交换法是指从两条路径中分别选择两点,然后互换它们的位置;1-2节点交换法是指从一条路径中选择一点,再从另一路径中选择两点,互换这一点与这两点的位置。本文在研究过程中将采用λ-interchange的1-0节点交换法和1-1节点交换法,并根据本研究需求可拆分及卸货时间窗约束的特点,对具体操作进行一定的改进。
1-0节点交换法即将一条路径上的某一点𝑖首先从路径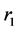 上删除,随后再将其插入到另一路径
上删除,随后再将其插入到另一路径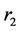 的最优位置,同时要满足𝑖在路径
的最优位置,同时要满足𝑖在路径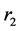 上的卸货时间窗及容量等约束。针对本研究特点,具体可分为以下两种情况讨论。
上的卸货时间窗及容量等约束。针对本研究特点,具体可分为以下两种情况讨论。
Senior1: ,计算
,计算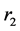 路径的剩余容量
路径的剩余容量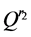 ,若
,若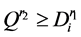 ,则将
,则将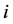 从路径
从路径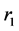 中删除,插入到路径
中删除,插入到路径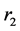 中去,并更新
中去,并更新 ,
,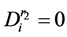 ;若
;若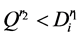 ,则将
,则将 插入到路径
插入到路径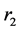 中,同时将其需求拆分为
中,同时将其需求拆分为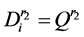 ,
, 。
。
Senior2: ,计算
,计算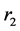 路径的剩余容量
路径的剩余容量 ,若
,若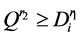 ,则将
,则将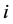 从路径
从路径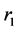 中删除,并更新
中删除,并更新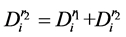 ,
,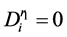 ;若
;若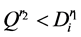 ,此时无法进行插入操作。
,此时无法进行插入操作。
1-1交换法即将一条路径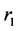 上的某一点i与另一路径
上的某一点i与另一路径 上的某点j的位置进行交换,同时需满足各项约束条件。针对所研究问题,具体可分为以下三种情况:
上的某点j的位置进行交换,同时需满足各项约束条件。针对所研究问题,具体可分为以下三种情况:
Senior3: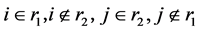 ,计算
,计算 路径的剩余容量
路径的剩余容量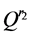 ,若
,若 ,则将
,则将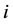 、
、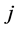 两点完全互换,并更新
两点完全互换,并更新 ,
,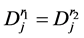 ,若
,若 ,则将
,则将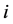 从路径
从路径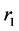 中删除,插入到路径
中删除,插入到路径 中,
中, ,将
,将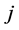 插入到
插入到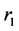 中,同时将其需求拆分为
中,同时将其需求拆分为 。
。
Senior4: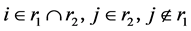 ,且
,且 ,则将
,则将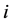 从路径
从路径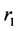 中删除,并更新
中删除,并更新 ,
,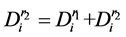 ,同时将
,同时将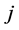 插入到
插入到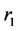 中,同时将其需求拆分为
中,同时将其需求拆分为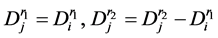 。
。
Senior5: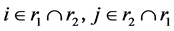 ,且
,且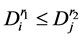 ,则将
,则将 从路径
从路径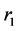 中删除,并更新
中删除,并更新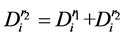 ,
, 点位置不变,同时将其需求拆分为
点位置不变,同时将其需求拆分为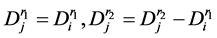 。
。
以上是构造邻域的几种不同的插入、交换的操作,但在算法实际应用过程中,需要制定一定的规则以确定每一步将采用哪种操作来构造邻域、产生候选集,并且当确定实施哪一种操作后,还需确定具体选择哪几条路径、哪几个点来进行操作。
对于以上问题,本研究采用如下的方法来解决:首先,本研究中设定侯选集的大小为 ,其中
,其中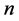 为问题中的节点数。即侯选集中包含有
为问题中的节点数。即侯选集中包含有 个由构造邻域而产生的邻居。这
个由构造邻域而产生的邻居。这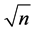 个邻居具体的产生方法为,首先在or-opt交换法、1-0节点交换法和1-1节点交换法中由计算机随机选取一个方法,确定采用的方法后,再由计算机随机选取一或两条路径中的几个供应商点,然后考察对其进行操作是否满足约束条件,若满足,则进行操作,一个邻居生成完毕;若不满足,则重新随机选择一个操作方法,并重新随机选取路径和点,直到生成一个新的邻居为止。以此随机的方法,逐一生成候选集中的十个邻居,并从中选择最好的一个考察其是否被禁忌、是否可特赦等,以替代当前解
个邻居具体的产生方法为,首先在or-opt交换法、1-0节点交换法和1-1节点交换法中由计算机随机选取一个方法,确定采用的方法后,再由计算机随机选取一或两条路径中的几个供应商点,然后考察对其进行操作是否满足约束条件,若满足,则进行操作,一个邻居生成完毕;若不满足,则重新随机选择一个操作方法,并重新随机选取路径和点,直到生成一个新的邻居为止。以此随机的方法,逐一生成候选集中的十个邻居,并从中选择最好的一个考察其是否被禁忌、是否可特赦等,以替代当前解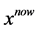 。
。
4.3.4. 禁忌对象及禁忌长度
对以上的邻域搜索方法,建立以解的向量分量为禁忌对象的禁忌表,具体如表1所示。
以上禁忌对象的禁忌长度均为 ,其中
,其中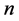 为问题中的节点数。
为问题中的节点数。
4.3.5. 特赦规则
本研究的特赦规则将采用基于评价值的规则,即当出现一个解 的评价值与已出现的最好解
的评价值与已出现的最好解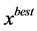 的评价值相比时,
的评价值相比时, ,则即使从
,则即使从 向
向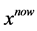 的变化是被禁忌的,此时也可以解禁。
的变化是被禁忌的,此时也可以解禁。
4.3.6. 终止规则
采用双重终止规则,即当总的迭代次数达到某一充分大的数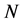 ,或者在某一给定的步数
,或者在某一给定的步数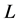 之内目前最好解没有改进,则算法终止。
之内目前最好解没有改进,则算法终止。
5. 算例和实验分析
在之前的VRPTW问题研究中,多数学者采用Solomon标准测试数据集对自身算法进行测试。本文所研究的需求可拆分情境下卸货时间窗约束的汽车零部件循环取货路径问题没有标准的测试数据集,因此本文同样采用Solomon测试数据来验证需求可拆分算法的有效性。
由于以往Solomon的实验中目标函数只考虑了系统形式距离的长短,因此,本文的实验同样将距离作为实验的目标函数,同时,我们假设汽车零部件的包装体积、重量等物理参数为标准统一的规格,运输所采用的车辆容量是以装载货物单位包装的数量为基本单位。
本实验采用Matlab语言编写程序进行模拟。硬件配置如下:CPU采用Intel Core i7-4720HQ @2.60 GHz;内存容量为8 GB,内存频率为1600 MHz。
实验将通过对比使用本文算法求解Solomon标准测试数据得到的最优解与目前已知的使用启发式算法得到的最佳近似解(不可拆分的情况下)及文献 [14] 所设计的禁忌搜索算法求得的最优解来验证本文算法的有效性。由于Solomon数据中没有引入卸货时间窗,本文选取各个供应商货物回到RDC节点的时间点上下浮动一个标准节点卸货时间来构建供应商卸货时间窗,对比结果如表2所示。

Table 2. The comparison of three algorithms in Solomon data
表2. Solomon数据三种算法最优解对比
续表
通过观察表2发现,在56组测试数据中,本文算法有33组最优解优于文献 [14] 或目前已知最好非拆分解,这充分证明了本文算法的有效性,特别是由于文献 [14] 也采用了拆分的方法,通过对比说明了本文拆分算法优于文献 [14] 的拆分算法。但是只对比本算法与目前已知最优非拆分算法的解就会发现,虽然本文算法在某些数据集合上更有优势,仍有部分不及目前已知最优解,其中R1、C1、RC1数据集中开放时间窗较窄,因此引入卸货时间窗后对解的优化有较好的效果,29组数据中有24组优于文献 [14] 的最优解,R2、C2、RC2数据集对供应商的开放时间窗较宽,因此对供应商取货时间的优化不明显,在27组数据中有17组优于文献 [14] 的最优解。此外,Solomon标准测试数据中设置的车辆容量较大,多数车辆在装载率较低的情况下就受限于时间窗约束返回RDC终止服务,会导致本算法计算时无法充分发挥需求可拆分的特点。
6. 结论
本文针对当今汽车零部件供货物流的循环取货路径规划问题,引入卸货时间窗的概念,提出需求可拆分的路径规划方案,并在此情景上建立数学模型,设计了改进的启发式算法对模型进行求解,通过采用Solomon标准测试数据验证了所设计算法的有效性,验证了卸货时间窗情境下,本算法可以有效提升Solomon标准数据中大部分路径规划解得质量。特别是在原数据中时间窗约束较窄的情况下,本拆分算法的优越性显著。此外,为方便计算,本文在验证算法有效性过程中假设汽车零部件的包装体积、重量等物理参数为标准统一的规格,运输所采用的车辆容量是以装载货物单位包装的数量为基本单位。在实际情况中,这一假设并不合理,此时可以考虑以货物和车辆的体积或质量为单位进行计算。同时,本文仅考虑了单一RDC、单一车型的情况。在后续研究中,可以加入多个RDC、多车型的情景,进一步考察本算法的性能,在商业领域,本文引入卸货时间窗概念,准确描述当今汽车零部件入厂物流中主机厂(RDC)占据主导地位确定到货时间,各供应商根据卸货时间窗决定自身装货时间的情景,在后续研究中可以进一步探索卸货时间窗对循环取货路径规划的系统影响。
致谢
本论文是在导师朱道立教授的悉心指导下完成的。老师渊博的专业知识,严谨的治学态度,精益求精的工作作风,诲人不倦的高尚师德,严以律己、宽以待人的崇高风范,朴实无华、平易近人的人格魅力对我影响深远。不仅是我树立了远大的学术目标、掌握了基本的研究方法,还使我明白了许多待人接物与人处事的道路。
同时我还要感谢我的同门师兄——赵磊。赵磊师兄在朱老师门下攻读博士,在算法领域上有所建树。在我遇到算法设计上的疑惑时,他总能细心的引导我找到解决问题的方法。
本论文从选题到完成,倾注了老师大量的心血,获得学长的耐心帮助。在此,谨向朱道立老师和赵磊学长表示崇高的敬意和衷心的感谢!