1. 引言
图像匹配是计算机视觉与图像处理领域中的关键问题,在遥感图像分析、视觉导航、目标识别等领域有着十分重要的应用。在各种图像特征中,直线特征反映了图像中的边缘信息,具有一定的不变性。目前,研究人员提出了许多基于直线段的图像匹配方法 [1] - [7] ,但由于仅利用了图像的局部结构信息,这些方法在处理具有较大旋转和平移的图像时,匹配性能有待提高。
近年来,采用图匹配(Graph Matching)来解决图像匹配问题受到越来越多的关注,典型方法有基于谱图理论的特征匹配方法 [8] [9] 。基于谱图理论的点匹配方法的主要思想是,将特征点匹配问题转化为联合图中的最大基团搜索问题:首先搜索潜在匹配点对,构造联合图,然后计算联合图节点之间的边的权值形成亲和性矩阵,最后根据亲和性矩阵的主特征向量来搜索联合图中的最大基团,从而得到最终的匹配点对。在此基础上,文献 [9] 通过利用图中点对之间的最短路径来构造亲和性矩阵元素,从而提高匹配方法的鲁棒性,但是该方法对最短路径的描述仅是采用边的距离权值,仍然不具有尺度不变性,因此不能处理具有较大几何畸变的图像匹配问题。
借鉴文献 [8] [9] 的思想,本文提出了一种基于图匹配的直线段方法,该方法以直线段为特征构造图,利用直线段对之间的关系建立图的边描述向量,再采用 [8] [9] 的图匹配方法实现直线段之间的匹配。实验结果表明,该方法能够较好地获得直线段之间的匹配关系,且能处理畸变较大的图像之间的匹配。
2. 基于图匹配的直线段匹配方法
对于图像中提取的直线段特征,利用其中点构造DT图,其中节点表示直线段,边表示两条线段之间的关系。因此,可以利用直线段之间的关系来建立图的边描述向量,进而建立图中节点之间的最短路径描述向量。
2.1. 基于直线段对关系的最短路径描述
对于基于直线段构造的DT图,采用直线段之间的关系 [10] [11] 来构造边的描述向量:1) 一条直线段的两个端点到另一条直线段的距离之比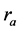 ;2) 两条直线段之间的夹角
;2) 两条直线段之间的夹角 ;3) 两条直线段之间的长度比
;3) 两条直线段之间的长度比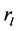 ;4) 两条直线段的平均梯度幅值之比
;4) 两条直线段的平均梯度幅值之比 。上述四个参数中,1) 为仿射不变量,2)、3) 为相似变换不变量,4) 理论上对所有几何变换保持不变,但对光照变化敏感。
。上述四个参数中,1) 为仿射不变量,2)、3) 为相似变换不变量,4) 理论上对所有几何变换保持不变,但对光照变化敏感。
如图1所示,对于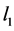 、
、 ,四种参数的定义如下:
,四种参数的定义如下:

Figure 1. Relationship between two line segments
图1. 直线段对之间的关系示意图
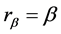 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
式(2)、(3)中,采用长度较短的直线段长度作为分子,目的是使得DT图的权值矩阵对称;式(4)中,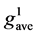 、
、 表示平均梯度幅度。上述参数中,参数
表示平均梯度幅度。上述参数中,参数 和参数
和参数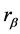 、
、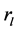 、
、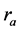 分别反映了直线段对的灰度信息和几何信息,其中
分别反映了直线段对的灰度信息和几何信息,其中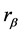 、
、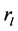 是相似不变量,
是相似不变量,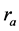 是仿射不变量。
是仿射不变量。
为了提高图的边的描述向量的独特性,采用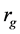 、
、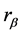 、
、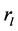 、
、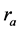 等四个参数来建立图的边的属性信息描述:
等四个参数来建立图的边的属性信息描述:
 (5)
(5)
对于基于直线段中点构造的DT图,假设节点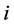 到节点
到节点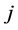 之间的最短路径用节点表示为
之间的最短路径用节点表示为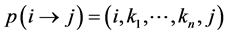 ,则最短路径上的边为
,则最短路径上的边为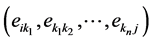 。根据式(5),此时最短路径的描述向量
。根据式(5),此时最短路径的描述向量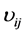 可以直接由路径上边的权值向量构造:
可以直接由路径上边的权值向量构造:
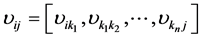 (6)
(6)
分开来表示,可以得到:
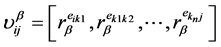 (7)
(7)
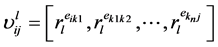 (8)
(8)
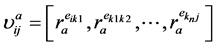 (9)
(9)
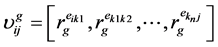 (10)
(10)
根据式(6)~(10),则针对直线段特征构造的最短路径描述向量为:
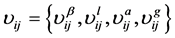 (11)
(11)
将式(11)中的4个描述向量依次从1~4编号,即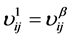 ,
,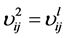 ,
, ,
,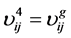 ,则两个图之间对应的路径的相似性度量由下式计算:
,则两个图之间对应的路径的相似性度量由下式计算:
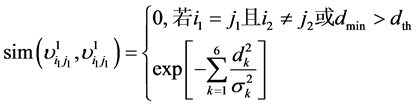 (12)
(12)
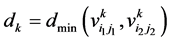 (13)
(13)
式中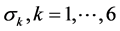 为衰减控制参数,将其设为两个图之间的所有最短路径之间距离
为衰减控制参数,将其设为两个图之间的所有最短路径之间距离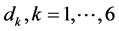 的平均值。
的平均值。
2.2. 算法流程
对于待匹配的图像对,采用边缘检测算子检测边缘并简化为直线段表示。对于待匹配的两组直线段特征,基于直线段的中点构造DT图,将图像匹配转化成了图匹配问题。
对于直线段的特征描述符,采用在DT图中与其连接的边的权值向量来描述。如图2所示,对于直线段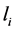 ,采用与其邻接的
,采用与其邻接的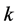 条直线段来描述,从邻接的最长直线段开始,沿逆时针方向依次标为
条直线段来描述,从邻接的最长直线段开始,沿逆时针方向依次标为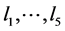 ,相应的边记为
,相应的边记为 ,则直线段的特征描述符为:
,则直线段的特征描述符为:
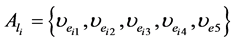 (14)
(14)
对于待匹配图像中提取的两组直线段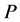 和
和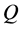 ,算法步骤如下:
,算法步骤如下:
1) 分别基于直线段的中点构造直线段 和
和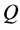 的DT图
的DT图 和
和 ,节点属性信息利用式(14)计算;
,节点属性信息利用式(14)计算;
2) 利用节点属性信息求解潜在匹配节点对,形成联合图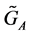 中的节点;
中的节点;
3) 计算联合图 节点之间的边的权值,即亲和性矩阵
节点之间的边的权值,即亲和性矩阵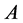 :对于联合图中的某两个节点(
:对于联合图中的某两个节点(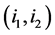 ,
,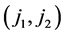 ),在图
),在图 和
和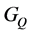 中找到最短路径
中找到最短路径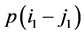 和
和 ,并构造路径的描述向量
,并构造路径的描述向量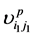 和
和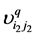 ,利用式(12)~(13)计算路径相似性;
,利用式(12)~(13)计算路径相似性;
4) 根据矩阵 ,采用谱图匹配法 [8] [9] 获得直线段之间的对应关系。
,采用谱图匹配法 [8] [9] 获得直线段之间的对应关系。
3. 实验分析
本节通过实验来验证算法的匹配性能,3.1节采用仿真图像,3.2节采用实际采集图像。
3.1. 实验一
实验一采用仿真图像,验证算法的鲁棒性。在大小为256 × 256空白图像上,随机构造服从均匀分布的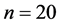 条直线段
条直线段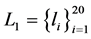 ,
,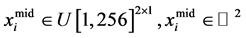 ,长度在
,长度在 内服从均匀分布,则直线段的两个端点为
内服从均匀分布,则直线段的两个端点为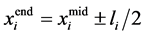 。
。
对于每条直线段的端点,加入位置误差:
 (15)
(15)
另外,向图像中随机增加不同数量的干扰直线段(图3)。
根据上述步骤,得到模板直线段集合 作为模板图像,其中
作为模板图像,其中 、
、 分别表示真实和干扰直线段。对
分别表示真实和干扰直线段。对 进行集合变换,得到待匹配直线段集合
进行集合变换,得到待匹配直线段集合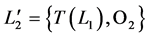 ,
,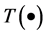 表示几何变换,以相似变换和仿射变换为例,如图4所示,其变换公式为:
表示几何变换,以相似变换和仿射变换为例,如图4所示,其变换公式为:
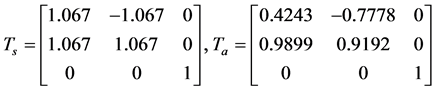 (16)
(16)
本文算法对于干扰直线段和位置误差的鲁棒性能分别如图4、图5所示。由图可以看出,本文算法
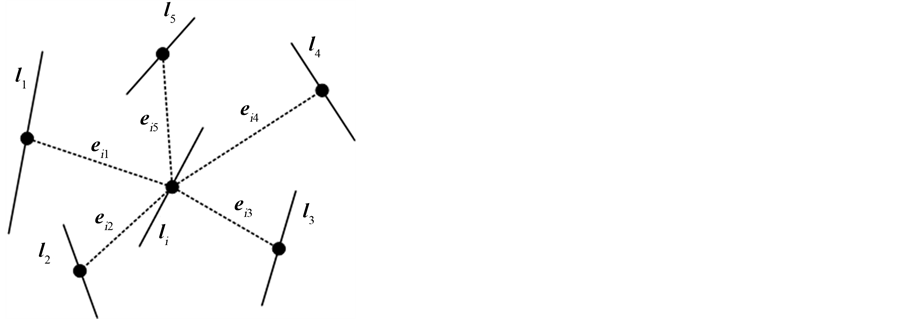
Figure 2. The neighbor line segments of a node in DT graph
图2. DT图中某直线段的邻接直线段


 (a) 仿真直线段集(模板图像) (b)相似变换(c)仿射变换
(a) 仿真直线段集(模板图像) (b)相似变换(c)仿射变换
Figure 3. Simulated line images
图3. 仿真图像生成
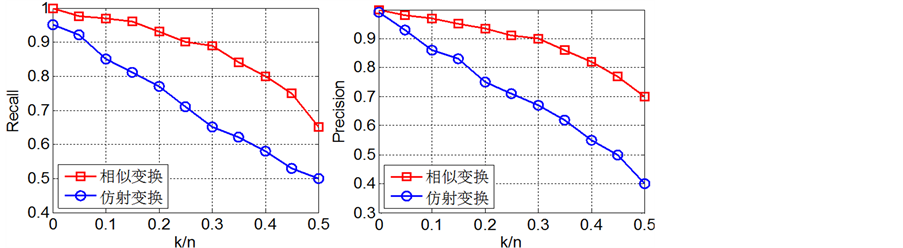 (a) Recall~k/n (b) Prcesion~k/n
(a) Recall~k/n (b) Prcesion~k/n
Figure 4. The impact of interference on performance
图4. 干扰个数对算法性能的影响
体现出了较好抗干扰性和误差鲁棒性:两种变换下,在干扰数目小于20%、位置误差小于4时,Recall值和Precision值都大于0.8。但也可以看出,当位置误差和干扰数目增大时,算法性能开始下降。另外,比较相似变换和放射变换下的性能可以发现,所提算法在相似变换下的性能优于仿射变换下的匹配性能。分析原因是,位置误差的增大、干扰数目的增多以及畸变程度的增加,会改变图像中直线段之间的邻接结构,从而使得路径描述向量发生变换,导致匹配性能下降。
3.2. 实验二
实验二采用实际图像验证算法的性能,如图6、图7所示,两组图像序列分别为相似变换(S)和仿射变换(A),每个序列的第一幅表示模板图像,其他为经过变换后的待匹配图像。
表1给出了各个待匹配图像中直线段的匹配结果,图8为图像A12的直线段匹配示意图。可以看出,
在实际图像中,本文所提匹配算法也取得了较好的匹配性能,而且在相似变换下的性能优于仿射变换,这与仿真图像中得到的结论一致,这是由仿射畸变的增大导致的。尽管在仿射畸变增大时,算法的准确率有所下降,但是如果我们考虑前5对直线段的匹配准确率,本文算法仍然保持了较高的准确率,即Precision~Top-5较高(大于0.95),这有利于基于少量特征实现图像配准。
4. 结论
本文提出了基于图匹配的直线段匹配方法,该方法较好地利用了直线段之间的结构关系信息,在初始匹配时比较的描述符是根据其与在DT图中邻接的直线段的关系构造的,相当于利用了图像的局部结
 (a) Recall~k/n (b) Prcesion~k/n
(a) Recall~k/n (b) Prcesion~k/n
Figure 5. The impact of position error on performance
图5. 位置误差对算法性能的影响



 (a) 模板图像(S1) (b) 待匹配图像S2 (c) 待匹配图像S3 (d) 待匹配图像S4
(a) 模板图像(S1) (b) 待匹配图像S2 (c) 待匹配图像S3 (d) 待匹配图像S4
Figure 6. Real images (similarity transform)
图6. 实际图像(相似变换)



 (a) 模板图像(A1) (b) 待匹配图像A2 (c) 待匹配图像A3 (d) 待匹配图像A4
(a) 模板图像(A1) (b) 待匹配图像A2 (c) 待匹配图像A3 (d) 待匹配图像A4
Figure 7. Real images (affine transform)
图7. 实际图像(仿射变换)

Table 1. Matching results of the two sequences
表1. 两组图像序列的匹配结果
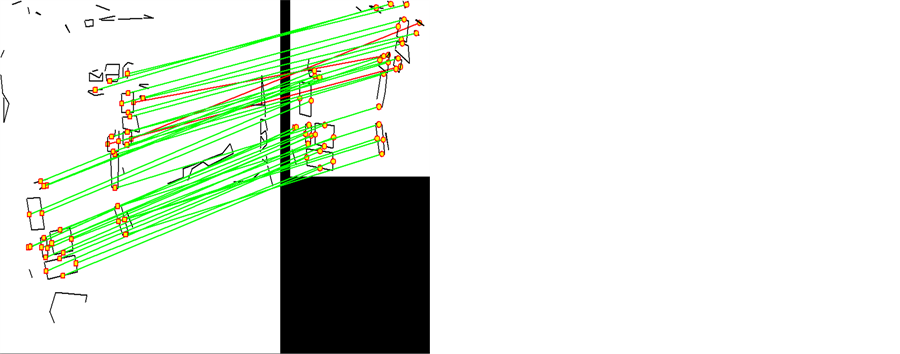
Figure 8. Matching illustration of line segments in images A12
图8. 图像对A12的直线段匹配示意图
构信息,而在实现图匹配时比较的是相应的最短路径的相似性,相当于利用了图像整体结构信息。实验分析表明,本文所提算法取得了较好的匹配性能和抗干扰性能。
基金项目
国家自然科学基金(编号61401504),博士后资助面上项目一等资助(2014M562562)。