1. 引言
随着计算机视觉领域的发展,图像拼接技术变成计算机图形学的一个重要的研究内容。对于不同的需要,将具有相同特征点的多幅图像拼接成一幅全景图 [1] ,实现在一幅图像上对于整个世界环境的观察。而图像拼接的首要问题就是图像匹配。图像匹配指的是,在不同的匹配场景下,使用不同的匹配算法,通过对数字图像的构成信息,包括了图像内容、图像的结构、特征、图像的纹理灰度等信息进行分析,达到在两幅或者多幅图像之间寻找同名点的目的。本文提出把PCA-SIFT算法用于图像拼接的匹配部分 [2] 。PCA-SIFT算法在描述子构建上作了创新,主要是将统计学中的主成分分析(PCA)应用于对描述子向量的降维,以提高匹配效率。
2. SIFT算法的特征匹配
随着对图像拼接的研究工作的不断深入,现今的各类匹配算法各具优劣,根据图像类型的差异往往选择不同的匹配算法,也就是说匹配算法的选择和图像本身的性质是强相关的,目前还不存在一种可以通用的处理各种类型图像之间的匹配问题的匹配算法,因此匹配算法的选定需要综合考虑匹配效果的好坏,匹配算法的准确性和计算所耗费的时间以及计算量的大小这一系列因素,以及考虑匹配算法对各种外界条件变化如光照改变、噪声影响、畸变影响等的敏感程度 [3] 。基于SIFT的特征匹配算法主要是由两个部分组成:首先构建SIFT特征向量,其次对SIFT特征向量进行匹配 [4] 。
a. 生成SIFT特征向量:SIFT特征向量的生成包括了构建尺度空间检测极值点、对极值点进行过滤和精确定位、为精确的关键点分配主方向形成向量、生成SIFT特征向量描述子这四个步骤 [5] :
第一步:生成不同的尺度空间,并且获取尺度空间的极值点
由于SIFT特征是一种尺度不变的特征,因此为了实现能够在不同尺度下对图像特征进行提取,首先使用高斯滤波函数与图像进行卷积运算得到图像在不同尺度空间下的高斯图像表示,高斯核是唯一一个能够实现尺度变换的变换核 [6] 。基于高斯核对图像进行处理的数学表示如下(1)所示:
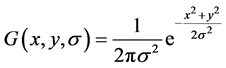 (1)
(1)
图像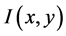 在不同尺度下的表示,即图像同不同尺度高斯核进行卷积运算,数学表达用公式(2)表示:
在不同尺度下的表示,即图像同不同尺度高斯核进行卷积运算,数学表达用公式(2)表示:
 (2)
(2)
L表示的即为图像的尺度空间, 为尺度因子,
为尺度因子, 即对应图像上的像素点。尺度因子越大表明反映的是图像的概貌特征,尺度因子越大,图像越模糊,尺度因子越小对应的是图像的细节特征,也即是说尺度因子越小,图像的分辨率越高 [7] 。
即对应图像上的像素点。尺度因子越大表明反映的是图像的概貌特征,尺度因子越大,图像越模糊,尺度因子越小对应的是图像的细节特征,也即是说尺度因子越小,图像的分辨率越高 [7] 。
根据上述构造尺度空间函数来建立高斯金字塔,设定高斯金字塔有O阶,每一阶有S层,相邻两阶之间的图像大小有一定的规律,即每一阶图像大小是前一阶图像大小的一半,在各阶的S层图像之间,图像大小是一致的,但是相邻层之间的尺度变换因子是不同的,每一层的尺度因子都是前面一层的K倍,如图1所示:
根据高斯金字塔构建差分高斯金字塔,即利用高斯金字塔每一阶中相邻两层的尺度空间函数相减构成差分高斯金字塔的每一层,如图1右所示。
为了检测极值点,需要在差分高斯金字塔中对每个采样点进行比较运算,采样点必须同它所在二维图像周围所有点,以及相邻尺度上下层的所有相邻点进行比较,如图2表示,处在中间位置的采样检测点就必须同上下层以及同层的相邻点进行比较,一共有九个点。这样就可以确保得到的极值点在二维图像中和尺度空间都为极值点。极值点的判断是指该点经过同范围内其他点的比较后结果是最大或者最小点。
第2步:过滤极值点,精确定位
过滤极值点为的是去掉一些低对比度和受噪声影响比较明显的点,并且一些不理想的边缘点也需要被排除,最终留下参与最后特征匹配的点,既是定义的关键点。过滤极值点采用的方法是Brown提出的,利用三维二次函数将极值点用泰勒展开,并且精确定位到亚像素级,尺度空间的泰勒展开形式如式(3):
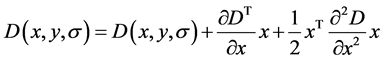 (3)
(3)
对 求偏导并令值为0可以获得极值点的位置表示:
求偏导并令值为0可以获得极值点的位置表示:
 (4)
(4)
结合上述两式可以得到:
 (5)
(5)
此时极值点的保留准则设定为: ,若满足该条件则该极值点保留,否则过滤。去除不理想的边缘点,则根据高斯差分极值点在穿越横跨不理想边缘会获得比较大的主曲率,而在垂直方向则有较小的主曲率这一特性 [6] 。根据Hessian矩阵(6)得到:
,若满足该条件则该极值点保留,否则过滤。去除不理想的边缘点,则根据高斯差分极值点在穿越横跨不理想边缘会获得比较大的主曲率,而在垂直方向则有较小的主曲率这一特性 [6] 。根据Hessian矩阵(6)得到:
 (6)
(6)
H的特征值的变化与D的主曲率变化一致,是正比的关系,取 作为最大特征值,
作为最大特征值, 为最小特征值,有如公式(4)和(5)表示:
为最小特征值,有如公式(4)和(5)表示:
 (7)
(7)
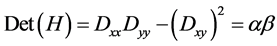 (8)
(8)
将 带入则有:
带入则有:
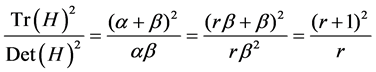 (9)
(9)
最终极值点被过滤与否取决于曲率同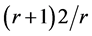 值的比较结果,曲率小于该值则保留作为关键点,否则认为该点位于不好的边缘而丢弃该点。
值的比较结果,曲率小于该值则保留作为关键点,否则认为该点位于不好的边缘而丢弃该点。
第3步:为关键点分配方向
在SIFT特征描述子生成过程中,加入主方向向量这一描述,即为每个关键点分配一个主方向,那么就可以保证关键点的旋转不变性。关键点的主方向的确定取决于其所在区域周围邻域像素的梯度方向,根据周围像素的方向分布特征,用统计直方图的方法,选取直方图中的峰值方向作为该关键点的主方向。关键点的梯度模值和梯度方向的计算公式分别如(10)和(11)所示:
 (10)
(10)
 (11)
(11)
m表示梯度取值大小,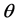 表示的是梯度方向。类比灰度直方图的定义,对相邻像素的梯度方向的处理也采用直方图进行统计的方式:直方图横轴代表的是像素梯度方向的大小,取值范围在0~360度,选取10度为一个单位,直方图的峰值则用来代表该点的主方向。
表示的是梯度方向。类比灰度直方图的定义,对相邻像素的梯度方向的处理也采用直方图进行统计的方式:直方图横轴代表的是像素梯度方向的大小,取值范围在0~360度,选取10度为一个单位,直方图的峰值则用来代表该点的主方向。
第4步:SIFT特征描述子的生成
为了获取完整的SIFT特征描述子,进而实现对SIFT关键点的详细描述,用图3中左方图所示表示关键点的邻域范围,即左图中的每个小的方格表示关键点的相邻区域的像素,每个小方格中的箭头表示该处像素的梯度方向,箭头长度的不同则表示梯度大小取值不同。由左右两图的关系可以看出,右图中的 方块中各个方块的梯度方向是根据左图中对应
方块中各个方块的梯度方向是根据左图中对应 区域方块像素梯度方向的累积得到的。而在实际的处理中,为了增加算法抵抗噪声的能力以及在匹配过程中为了保持较好的稳定性和健壮性,常常把关键点的邻域范围设定为
区域方块像素梯度方向的累积得到的。而在实际的处理中,为了增加算法抵抗噪声的能力以及在匹配过程中为了保持较好的稳定性和健壮性,常常把关键点的邻域范围设定为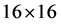 的区域,这样按下面右图所示的种子点形成方式,可以形成规格为
的区域,这样按下面右图所示的种子点形成方式,可以形成规格为 的种子点,种子点的个数综合梯度方向梯度大小等信息,实现对关键点的描述,即对每一个关键点的描述被定义在一个特征向量中,该向量维数是
的种子点,种子点的个数综合梯度方向梯度大小等信息,实现对关键点的描述,即对每一个关键点的描述被定义在一个特征向量中,该向量维数是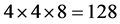 维,此向量即被称为SIFT特征描述子。
维,此向量即被称为SIFT特征描述子。

Figure 3. To generate the key direction
图3. 关键点方向生成
b. SIFT特征匹配:完成SIFT特征向量的生成后,要寻找合适的比较方法对特征向量进行对比以获得对应关系,从而完成匹配。对SIFT特征向量的匹配在于寻找一种相似性测度,比如构建相似性度量函数,当函数取得最小值时表明参与对比的两者之间相似程度越高,那么就可以确定二者的匹配关系。对SIFT特征的相似度量,由于SIFT特征是128维的向量,对比两个向量之间的相似性可以使用向量的相关知识,即用向量之间的距离来反映。利用距离来度量二者之间的相似程度,经常使用的几种距离有:
1) 欧式几何距离:
 (12)
(12)
2) 余弦相似度距离:
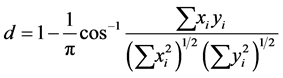 (13)
(13)
3) 绝对值距离:
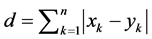 (14)
(14)
对SIFT描述子特征向量相似度的判定采用欧式几何距离。如果两个向量完全相同,那么他们的欧式距离便是0。因此在得到SIFT特征向量之后,Lowe提出采用优先搜索算法K-D树搜索与该特征向量最接近的几个特征点,设定某一阈值用来判定最近的距离值同次近的距离值的比值是否满足条件,在小于该阈值范围内则认定为有效的匹配点,该方法称为SIFT特征匹配,这种采用最近距离与次近距离的比值作为匹配点对的判定条件的搜索方法定义为BBF (Best Bin First)算法,该算法得到的匹配点集即为基于SIFT特征匹配算法得到的匹配结果。
3. 本文的方法
PCA-SIFT算法的前期步骤(检测特征点、修正、计算主方向)与传统SIFT相同,区别在于描述子的构建。步骤如下:
1) 构建描述子的区域选定为以特征点为中心的 矩形(已与特征点主方向对齐)。
矩形(已与特征点主方向对齐)。
2) 计算39 × 9矩形内每个像素对水平、垂直两个方向的偏导数(最外层像素不计算偏导数)。得到一个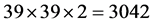 维的向量,对其归一化。
维的向量,对其归一化。
3) 假设有N个特征点,那么所有特征点描述子向量构成一个 的矩阵。对这N个向量计算
的矩阵。对这N个向量计算 协方差矩阵。
协方差矩阵。
4) 计算协方差矩阵的前k个最大特征值所对应的特征向量,这k个向量组成一个 的投影矩阵。
的投影矩阵。
5) 将 的描述子矩阵与
的描述子矩阵与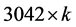 的投影矩阵相乘,得到
的投影矩阵相乘,得到 的矩阵,即降维描述子向量组成的矩阵。此时N个特征点的描述子向量均为k维,
的矩阵,即降维描述子向量组成的矩阵。此时N个特征点的描述子向量均为k维, 。
。
6) 利用RANSAC算法除去误匹配点。RANSAC算法的基本原理在于从观测数据样本集即获得的匹配点集中(包含了正确匹配的点也包含了错误匹配的点)选取一定数目的样本子集,通过子集中的数据对计算出符合数据之间变化的变化模型,并在观测数据样本集中检测该变化模型的符合程度,计算符合的该变化模型的数据数目,通过更新数据数目和计算误差概率来决定是否继续迭代或者决策符合当前模型的匹配点集为最优匹配 [8] 。具体实现步骤如下:
a) 根据实际的情况,从观测数据即得到的匹配数据集中选取一定数目的匹配点对作为样本子集。结合待匹配图像之间的具体变换类型决定子集所需最少匹配点对的数目 [9] 。
b) 使用样本子集中的匹配点对来计算,得到符合匹配点对之间坐标变换的变换矩阵M。
c) 在观测数据集中对该求得的变换矩阵进行验证,设定一定的误差允许范围,对观测数据集中的数据,与变换矩阵进行相似性度量的计算,误差在一定范围内视为符合该变换矩阵的数据元素,统计数据集中满足该变换矩阵的数据元素个数。
d) 将上一步骤中得到的数据元素个数同原有的最多数据元素个数比较,若本次数据元素个数多于原有值则更新本次数据为最优值,并且本次选取的数据子集以及相应的变换矩阵为最优一致集 [10] 。
e) 计算本次的误差概率值,该值同预先设定的允许的最小误差值进行比较,若大于最小允许误差值则继续进行步骤1到步骤4的迭代,直到误差值小于最小允许误差,此时算法停止。
7) 用Ransac算法将误匹配的特征点剔除,进而提高匹配的精度,得到第二次匹配的特征点集合 [11] 。最后再用最小二乘法最大程度的拟合所有数据点,使得优化后的图像匹配的数据点最靠近真实的点,最后进行拼接 [12] 。
4. 实验结果
1) 对尺度发生缩放的图像进行PCA-SIFT特征匹配,实验效果如图4~图6所示。
2) 对视角发生变化的图像进行PCA-SIFT特征匹配,实验效果如图7~图8所示。
3) 使用PCA-SIFT完成图像拼接,实验效果如图9所示。
PCA-SIFT与标准SIFT有相同的亚像素位置(sub-pixel),尺度(scale)和主方向(dominant orientations),但在计算描述子的时候,它用特征点周围的 的像斑计算它的主元,并用PCA-SIFT将原来的
的像斑计算它的主元,并用PCA-SIFT将原来的

Figure 6. Scale narrowed the image PCA-SIFT match result
图6. 尺度缩放的图像PCA- SIFT匹配结果

Figure 9. PCA-SIFT image stitching
图9. PCA-SIFT图像拼接
 维的向量降成20维,以达到更精确的表示方式。
维的向量降成20维,以达到更精确的表示方式。
实验表明PCA-SIFT所得的描述子在旋转、尺度变换,透视变换,添加噪声匹配的情形下,匹配均大幅领先于SIFT;在亮度变换时,与传统SIFT不相上下。在匹配时所得的正确点对也多于传统SIFT。可见PCA-SIFT生成的描述子质量很高。SIFT和PCA-SIFT的比较。在运行时间方面,PCA-SIFT在特征点提取、描述子计算中略快于SIFT;但在后续的描述子匹配过程中,PCA-SIFT的速度大大超过SIFT的速度。
5. 结束语
本文首先对SIFT 算法进行了介绍,并且指出了SIFT 算法的优点和不足。然后针对SIFT 算法的不足引出了一种优化后的算法PCA-SIFT。通过实验表明PCA-SIFT不仅保存了SIFT 算法的优点,而且降低了SIFT描述子的维度,使得图像拼接的速度更快、效果更好。
基金项目
国家863计划项目(2015AA016405)。