1. 引言
风洞试验 [1] 作为目前飞行器研制的最重要手段，风洞试验结果的可靠度直接影响飞行器的设计以及其气动性能。目前飞行器进行风洞试验时采用的支撑方式主要是传统的硬式支撑：尾部支撑、侧壁支撑、背部支撑和腹部支撑。近年来随着并联支撑系统的发展，绳牵引并联机构作为一种软式支撑在风洞试验中优势越发显著，绳索对模型周围流场干扰小且容易实现高速及复杂运动规律的运动，使其发展研究及应用备受关注。
目前已知的研究进展主要有国外法国国家航空研究局支持的“SACSO项目”，研究工作已经开展了多年，成功将绳牵引并联机构应用于立式风洞试验中 [2] [3] 。国内方面研究，文献 [4] 对绳牵引并联支撑系统国内研究情况进行了介绍。文献 [5] 利用张线支撑研究硬式支撑干扰问题。文献 [6] 构建了一整套风洞试验绳牵引六自由度并联支撑系统，采用拉力传感器在牵引绳上测得绳拉力，用于解算相关气动参数。针对绳索的流致振动可能对支撑系统运动精度的影响需要做进一步研究。
文献 [7] 分别从改进离散格式，构建流固耦合边界数据传递新方法等研究了柔性结构的流固耦合风效应问题。文献 [8] 研究了斜拉索的气动特性。文献 [9] [10] 基于流固耦合分析了长单索结构风致振动响应的特点。文献 [11] 研究了海洋悬跨管道、深海采矿系统中的输送软管、水中悬浮隧道等细长柔性结构在水中的流固耦合振动特性。文献 [12] 引入流体运动控制方程和大涡模拟湍流模式，提出风与结构的流固耦合方程的迭代求解过程，研究大跨度柔性空间结构的表面风压和流固耦合效应。文献 [13] [14] 分析长斜拉索风致振动情况，并针对索结构的振动控制做了相关研究。本文中的绳牵引并联支撑系统主要应用于飞行器模型的风洞试验，由于风洞试验中对飞行器位姿的精准度要求比较高，因此对于支撑系统中柔性绳索在低速来流情况下绳流固耦合振动的相关研究显得尤为重要。
绳牵引系统应用于风洞试验时，其绳在来流状态下和流场会有一定程度上的耦合情况，由于支撑系统的牵引绳直径很小，因此流固耦合 [15] 基本表现为流场对绳的影响，来流状态下致使绳变形的情况可能会影响飞行器位姿。因此本文主要对绳牵引系统中牵引绳的流固耦合情况做了相关研究。
2. 流固耦合控制方程及其理论基础
流固耦合控制方程主要由两部分组成，流体控制方程和固体控制方程。
2.1. 流体控制方程
流体流动遵循基本的守恒定律，本文主要涉及为低速不可压流动，选用的是无量纲化的N-S方程组：
(1)
式中的四项依次为瞬态项、对流项、源项和扩散项。
2.2.固体控制方程
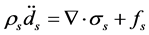(2)
表示固体密度，
表示固体域当地加速度矢量，
柯西应力张量，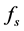
体积力矢量。
2.3. 流固耦合基本理论
流固耦合针对其控制方程的解法不同可分为强耦合和弱耦合 [16] 。强耦合法主要是构造流体域和固体域统一方程并在同一时间步内对流体变量及固体变量进行求解，并将求解结果用于下一时间步计算。此方法计算精度高，由于其对计算资源要求高，因此不适合用于计算解决复杂工程问题，比较适用于耦合场的理论分析。弱耦合法在同一时间步内对流体域和固体域分别单独进行计算，然后通过流固耦合交界面相互传递流体域和固体域解算结果，从而实现耦合求解。
从对流固耦合交界面信息传递的处理方法不同又可分为单向流固耦合和双向流固耦合。单向耦合是指流固耦合分析中耦合交界面数据传递是单向的，主要是把CFD分析计算流场结果传递给固体结构分析，固体结构分析数据不会传递给流场。双向流固耦合分析方法既考虑了流场对固体结构产生的风压作用，又考虑了结构受荷载响应后对流场分布的影响。
3. 绳牵引并联支撑系统
绳牵引并联机构做为风洞试验飞行器模型的支撑系统，可实现飞行器模型的六自由度运动，其原理样机结构如图1所示。考虑到系统的刚度与稳定性，飞行器模型由八根绳支撑起来，悬挂在空中。八根牵引绳分前后两组，每组四根。通过改变支撑牵引绳的长度可实现锥体模型的六自由度运动，以满足风洞试验对模型不同姿态的控制。锥体模型上分别有八个牵引点P1~P8，牵引绳系分别与之连接，然后通过各自对应的万向滑轮(B1~B8)变向，之后分别与各自对应的滚轴丝杠上的滑块相连。工控机通过分别控制八个伺服电机来带动电机上滑块运动，实现支撑绳的伸长缩短以控制模型姿态变化。
4. 不同预紧力对绳振动情况影响
绳牵引并联机构应用于风洞试验中，由于绳是柔性体，因此将其做为飞行器模型的支撑方式需要对绳施加预紧力。预紧力选取太小将无法满足试验需要，影响试验结果，预紧力选取过大又会影响牵引绳的使用寿命。针对预紧力选取问题，本文分别就单绳受不同预紧力时来流致使其变形情况分析，以选取最优预紧力大小。
4.1. 计算域和绳的位姿
本文主要分析单根绳在流场中情况，算例模型如图2所示，α表示绳倾角，β表示风向角，箭头所指表示来流方向。绳的选取长度为600 mm，直径为1 mm，弹性模量为43.9 GPa，泊松比为0.3，密度为1440 kg/m3。绳的属性选取主要参考我们实验所用凯夫拉5号线的材料属性所得。计算流场的大小选取：长 × 宽 × 高为1 m × 1 m × 1 m。
4.2. 流场网格划分和边界条件设置
本文来流流速选取为17 m/s，根据来流情况以绳直径为特征长度，对应的雷诺数为1100，此时流场
为不可压层流流动。流场整体网格如图3所示，网格总量为34万左右。绳周围进行了网格加密，第一层网格高度为0.2 mm，边界层为10层。
流场边界条件设置，流场为层流流动，因此，湍流模型的选取为层流。来流进口采用速度进口；出口为压力出口，参考压力值为零；壁面条件设置均采用自由滑移壁面；绳表面采用无滑移壁面条件。
4.3. 不同预紧力仿真分析及结果
预紧力的选取，本文采用的是ANSYS workbench里的单向流固耦合模块(弱耦合)，分别利用fluent进行CFD计算，ANSYS进行固体分析，然后将流场计算所得绳周围压力分布情况通过流固耦合交界面传递给绳，用于牵引绳的固体分析。
此处采用的绳流场布置情况为
。绳的约束采用两端铰接，并施加大小分别为2 N，50 N，70 N的预紧力，分析计算结果。
流体计算的结果绳周围压力场分布如图4所示。绳的前缘迎风面压力较大，绳的左右两侧及绳尾流处出现低压区。之后将流场信息通过流固耦合面以压力的形式传递给绳，得到绳的振动情况。绳在不同预紧力状况下的最大振动位移点基本在接近绳中点位置处。
施加预紧力大小分别为2 N，50 N，70 N等三种情况时绳的振动位移情况如表1所示。
Figure 2. Cable’s position in the fluid field
图2. 绳在流场中位置
由上述情况可知，在绳预紧力较小时，流场对绳振动影响相对较大。当绳预紧力大到足以使绳绷紧时，流场对绳的影响变得很小。继续增大绳预紧力，能继续改善流场对绳振动的影响，不过变化量已经小到可以忽略。所以，综合考虑在既能满足试验需求的情况下，又提高绳的使用寿命，选择预紧力为50 N即可。
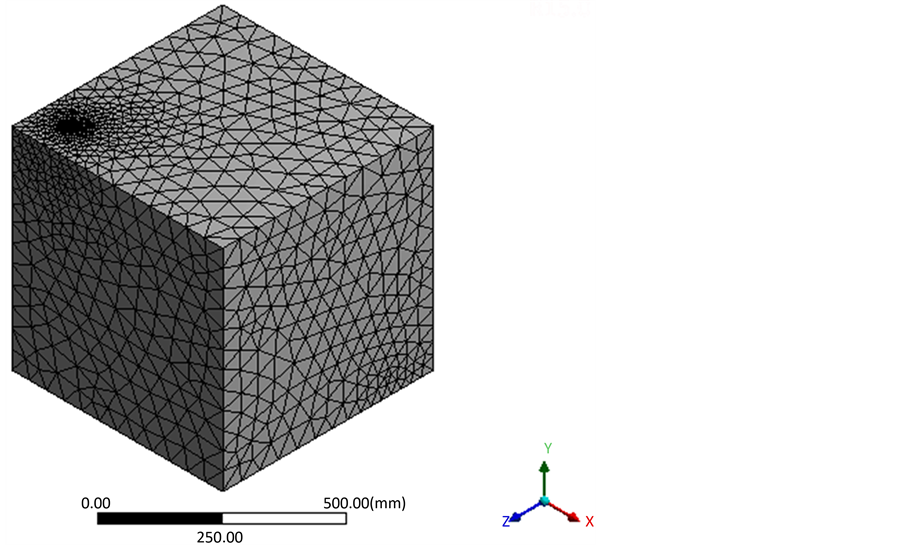
Figure 3. Mesh generation of fluid field
图3. 流场网格划分
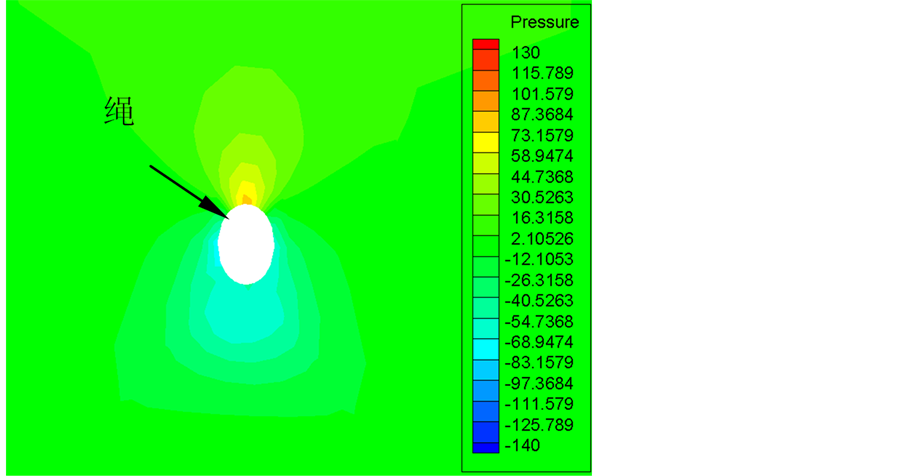
Figure 4. Pressure distribution around the cable
图4. 绳周围流场压力图
5. 不同工况下单绳流固耦合分析
本文主要借助已有商用软件ANSYS workbench下的流体力学计算软件CFX和结构分析软件ANSYS结合对不同工况下牵引绳进行双向流固耦合计算(弱耦合)，如图5所示。
绳的相关设置：两端采用铰接约束，在绳端添加50N预紧力，模拟绳拉紧状态。分别仿真计算了几种不同工况下绳的振动情况。
工况一：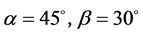
如图6所示，沿绳向振动位移情况，最大位移基本在绳中点位置处，最大位移值为0.102 mm。如图7所示选取的是绳最大位移点处的位移随时间的变化。绳主要表现为x方向上的振动，其次表现为y方向，z方向绳振动最小。当然这和来流风向角也有一定关系，来流风向角不同，绳的各个方向振动情况有一定差别。绳的振动周期为0.0085 s，振动随时间的变化表现为衰减的特性，但此计算模型中并未添加任何阻尼，这种情况主要由于空气的气弹性阻尼效应所引起，由此表现为绳周围空气对绳振动起一个反向抑制的作用，使得绳振动随时间衰减。
工况二：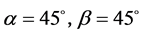
如图8所示，绳各节点处位移情况。由于绳的两端为铰接约束，因此两端处位移几乎为零，随着远离两端点位置，绳的振动位移逐渐变大，最大位移基本在绳中间位置，最大位移值为0.113 mm。如图9，绳振动主要表现为x方向上，y方向和z方向绳振动大小基本一样。绳振动受空气的气弹性阻尼效应影响，因此在未添加任何阻尼的情况下，绳振动表现为振幅衰减。振动周期为0.0085 s，由此可见绳振动周期不会受位姿的影响。
Table 1. Displacement of the maximum vibration displacement point with different pre-tension of cable
表1. 不同预紧力时绳最大位移节点处位移
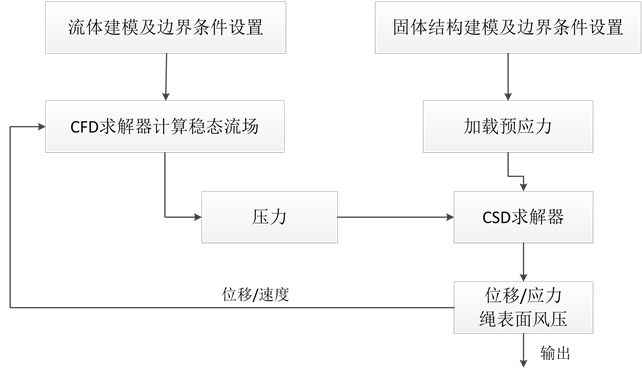
Figure 5. Flow chart of the bidirectional fluid-structure interaction analysis procedure
图5. 双向流固耦合计算流程图
由上述不同情况可以知：流场中绳最大振动位移基本在绳中点位置处；绳在流场中的不同角度布置，对绳振动最大值会有一定影响，但影响较小；流场致使绳变形，变形量相对较小，基本可以忽略其对绳的影响。
6. 结论
本文分别就绳牵引并联机构牵引绳在低速流场中预紧力的选取，以及绳的不同位姿下流固耦合情况做了相关研究，得出以下结论：
(1) 在来流速度为17 m/s状态下，绳的预紧力选取为50 N，基本可以满足工作状态。
(2) 低速来流时引起的绳振动变形较小，绳的气弹阻尼效应为正，对牵引绳的动力响应起抑制作用，使绳的振动表现出随时间衰减的特性。
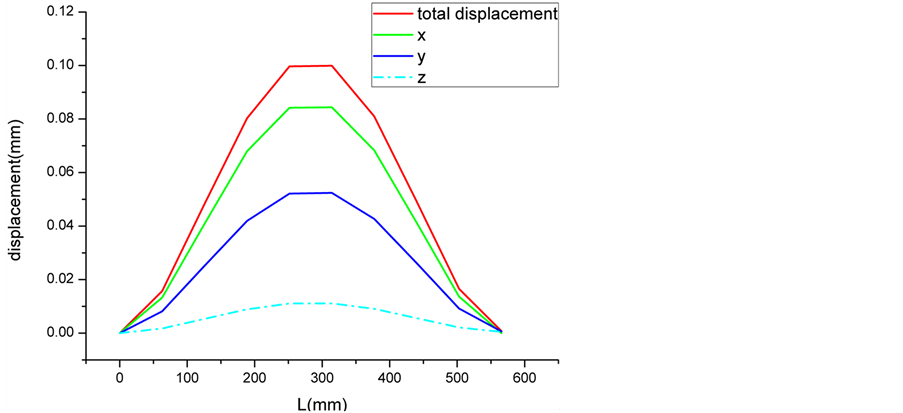
Figure 6. The vibration displacement of every point of the cable
图6. 绳各节点处的位移
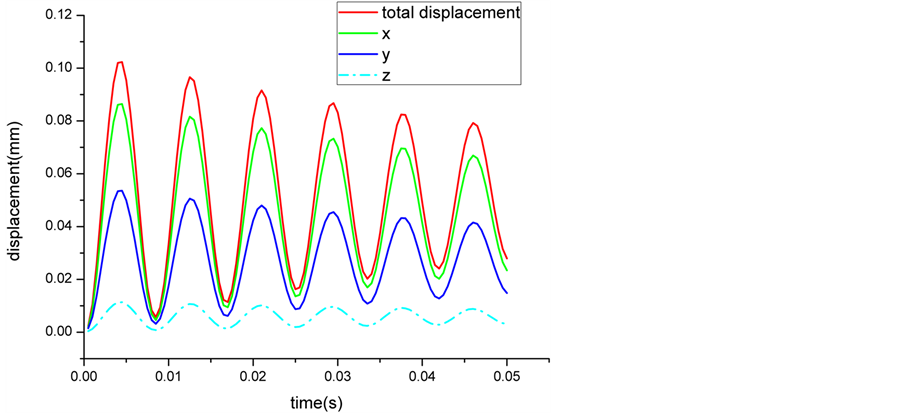
Figure 7. Time-history curves of the maximum vibration displacement point
图7. 最大振动位移节点处的位移随时间变化
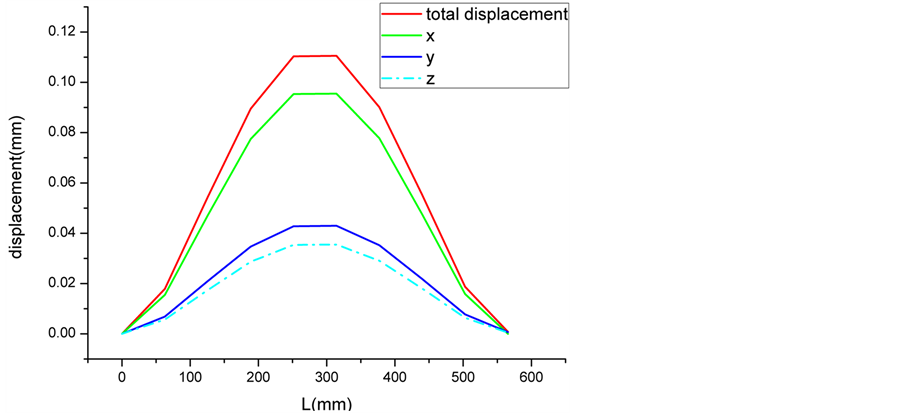
Figure 8. The vibration displacement of every point of the cable
图8. 绳各节点处的位移
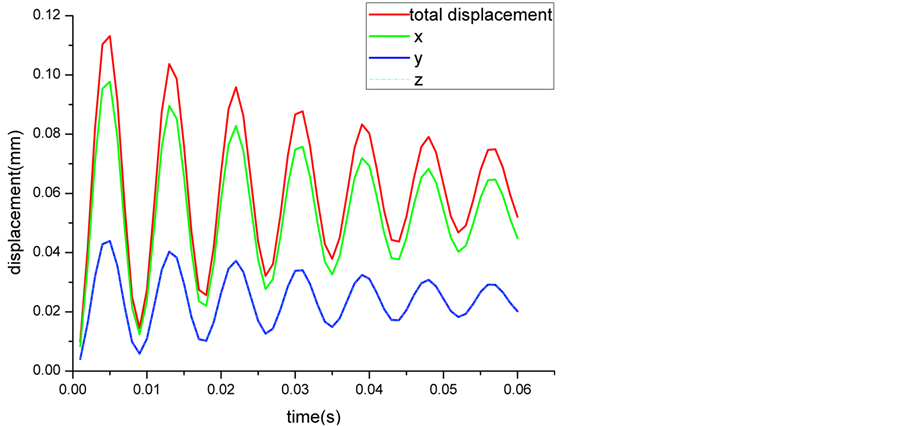
Figure 9. Time-history curves of the maximum vibration displacement point
图9. 最大振动位移节点处的位移随时间变化
(3) 来流致使绳振动的最大位移基本点基本在绳的中点位置处，绳在流场中的位姿不同，会对绳振动最大值有一定影响，但影响较小。进一步说明了绳牵引并联机构应用于低速风洞试验的可行性。
基金项目
国家自然科学基金资助项目(11472234)。