摘要:
利用Borel-Cantelli引理得到一个对M-值随机序列普遍成立的滑动平均的强极限定理。值得注意的是,本文中的结论对随机变量的相依性无任何要求。
Abstract:
By using the classical Borel-Cantelli lemma, we obtain a general founded strong limit theorem for M-value random sequences on moving average. It is noticeable that the conclusion in this paper has no requirement of the random variables.
1. 引言
强极限定理是概率论极限理论中一个极其重要的方向。二十世纪六十年代,独立随机序列的极限理论在Gnegenko和Kolmogrove等学者的共同努力下获得了完善的发展。此后,各种混和随机序列、相依随机序列,以及鞅的理论有了很大发展,其主要成果可参考文献 [1] [2] [3] 及其序列文献。我国学者在这方面也做出了许多出色的工作,在国际上也有一定的影响,参见 [4] 。本文得到一个对M值随机序列滑动平均普遍成立的强极限定理,推广了 [5] 中的结果。值得注意的是,本文中的结论对随机变量的相依性没有任何要求。
定义 设 是定义在概率空间
是定义在概率空间 上的一随机序列,其联合分布为
上的一随机序列,其联合分布为
 , (1)
, (1)
称 为M值随机序列。
为M值随机序列。
2. 主要结论
引理 [6] 设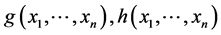 是概率空间
是概率空间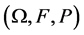 上的两个概率函数,
上的两个概率函数,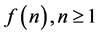 是列单调递增的取整数值序列,且
是列单调递增的取整数值序列,且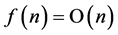 。令
。令
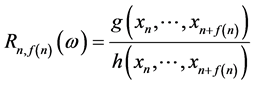 ,
,
则
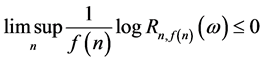 a.s.
a.s.
定理 设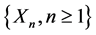 是由(1)定义的r.v.序列,
是由(1)定义的r.v.序列, 满足引理的条件。记
满足引理的条件。记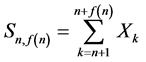 ,则
,则
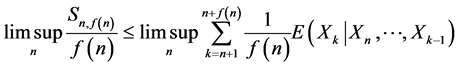 a.s. (2)
a.s. (2)
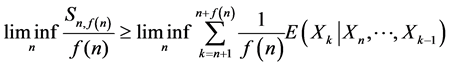 a.s. (3)
a.s. (3)
证 设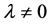 ,定义函数如下:
,定义函数如下:
 (4)
(4)
易知,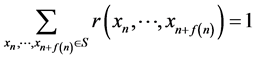
令
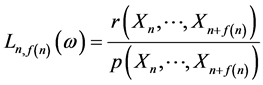 , (5)
, (5)
由引理,知
 a.s..(6)
a.s..(6)
由(4),(5),(6)有
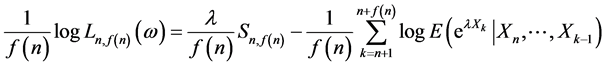 a.s..
a.s..
取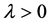 并使
并使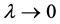 ,由
,由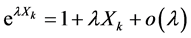 及不等式
及不等式 和(6)式,有
和(6)式,有
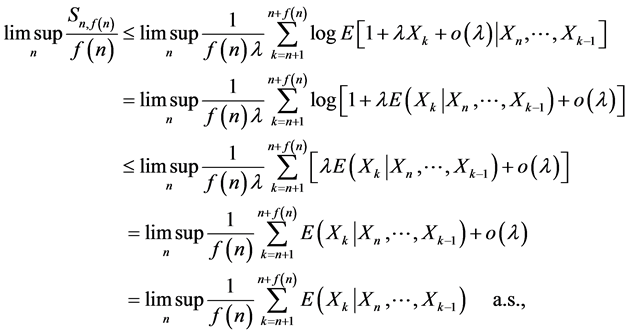
故(2)式成立。取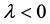 并使
并使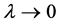 ,由(6)式,有
,由(6)式,有

故(3)式成立,定理证毕。
推论1 设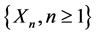 是一列取值于
是一列取值于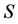 的独立随机变量序列,则
的独立随机变量序列,则
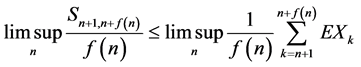 a.s.
a.s.
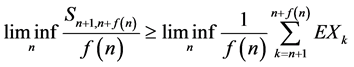 a.s.
a.s.
推论2 设 是一列取值于
是一列取值于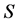 的独立同分布随机变量序列,则
的独立同分布随机变量序列,则
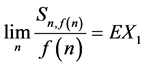 a.s.
a.s.
基金项目
安徽工业大学研究生创新基金资助(2015130)。
NOTES
*通讯作者。