1. 引言
随着发电需求量逐日加大、水资源紧缺现状日益加重,对水利工程建设的依赖也日趋增加。然而,大坝等水工建筑物的修建阻断了河流的连续性,改变了河流固有的自然特性,阻断了鱼类的洄游通道。鱼道是沟通鱼类洄游通道的一种有效措施。
鱼道主要有3种类型,即丹尼尔式鱼道、池堰式鱼道和竖缝式鱼道 [1] 。丹尼尔式鱼道,适合于跳跃能力强的鱼类;而堰流式鱼道,适合跳跃能力强的鱼类 [2] 。我国在2000年以来经过技术评估的24个国家级水利水电项目鱼道建设中,垂直竖缝式占到了58.3%,目前我国以垂直竖缝式鱼道为主 [3] 。
2. 国内外研究现状
2.1. 国外鱼道研究现状
竖缝式鱼道最早应用于加拿大Fraser河鬼门(Hell’s Gate)峡的鱼道中,对于竖缝式鱼道的水力特性与设计方法,国外学者进行了较多的研究。Rajaratnam等人 [4] 对竖缝式鱼道的均匀流和非均匀流特性进行了试验研究,得出无量纲流量与相对水深的关系。Wu等人 [5] 竖缝式鱼道的流场结构进行了试验,研究了竖缝式鱼道的消能效率,认为通过竖缝的流动可看作平面射流,但与平面射流又有很大区别;Guiny等人 [6] 对竖缝式鱼道的水力特性进行了数值模拟计算。
2.2. 国内鱼道研究现状
在国内,毛熹等人 [7] 对竖缝式鱼道提出了一种优化的新结构,使每一级鱼池都具有三级跌坎及一个凹槽,优化鱼道相比于原模型,鱼道内的平均流速降低了30%以上,水流也更为平缓。董志勇等人 [8] 分析了异侧竖缝式鱼道的横向流速分布的特征及其随流量的变化情况,得出了鱼池横向流速分布的特征表现为:在前半池长,近似为壁面射流分布;在后半池长,近似为高斯分布;横向流速分布特征几乎不随流量的变化。
另外,我国现在也有许多水利水电工程采用竖缝式鱼道作为鱼道工程类型,比如,辽宁三湾水利枢纽 [9] 、吉林老龙口水利枢纽 [10] 、北京上庄新闸 [11] 等。
3. 竖缝式鱼道模型试验
3.1. 模型尺寸
模型按照非1:1的比例进行时,对试验数据结果会有一定的误差,为了使试验数据结果更为精确,采用1:1的试验模型如图1所示,其更加地能体现出真实状态下的鱼道的模型的水流特征,能够提供更为准确的试验数据。
鱼道是提供鱼类洄游的通道,若要使鱼类的洄游更加地顺利,需要满足适合鱼类洄游各个条件,其
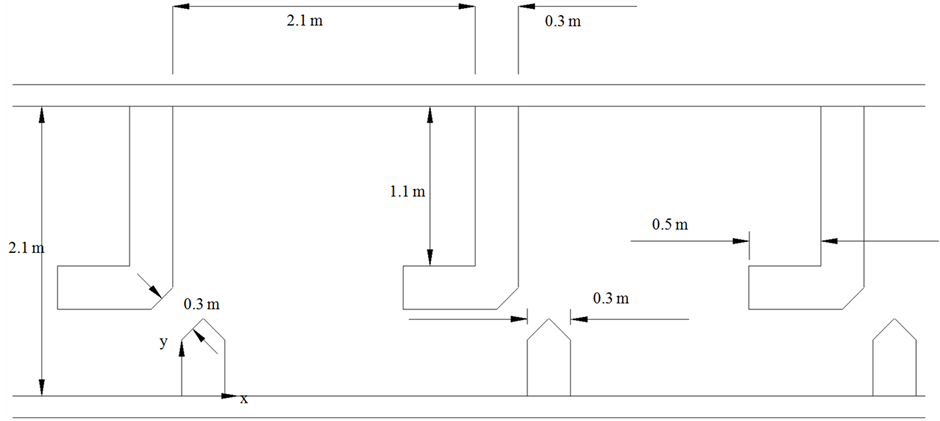
Figure 1. The model size of the fishway
图1. 鱼道的模型尺寸示意图
中流速极为重要,在鱼类洄游的路径之中出现了流速超过了鱼类洄游的最大游泳能力下的游速,鱼道是很难使鱼类顺利完成洄游的。此次试验将对鱼道的主流流速进行数据记录。
3.2. 试验设备与量测方法
3.2.1. 试验设备
试验所使用的试验设备为声学多普勒点式流速仪(小威龙),小威龙是一款高精度三维点式流速仪,应用范围十分广泛。小威龙采用声学多普勒测量原理,测量数据精度高,而且仪器本身不产生零点漂移。测量水深时精度可达0.001 m,测量流速时精度可达0.0001 m/s。因此精度要求完全可以满足试验要求。
3.2.2. 试验测量方法
试验模型由9个鱼池组成,每级鱼池布置34个测点,在各测点用小威龙进行测量。最终得到数据,分析数据,得到该鱼道主流流速的大小。
4. 试验结果及分析
4.1. 鱼道沿程流速变化
鱼道向下游方向设为x轴,垂直鱼道为y轴,如表1所示。
由图2可以得到,流速沿程一直处于波动状态,但是结合到该试验的试验模型的长度2.4 m,便能发现波动几乎是按照一个鱼池的长度2.4 m呈现出周期性的波动。并且每一个鱼池的最大流速相对上一个鱼池的最大流速有减弱的趋势。
由水力学知识,水流的连续性方程为: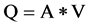 ,其中,Q为流量,在此次试验中为一个定值。当水流经过两个异侧竖缝的时候,过水面积为最小值,此时便有了流速V的最大值,随后断面面积增大,流速V又减小,然后水流流速就会重复这样的周期进行变化,这便是每一个鱼池流速波动的原因。
,其中,Q为流量,在此次试验中为一个定值。当水流经过两个异侧竖缝的时候,过水面积为最小值,此时便有了流速V的最大值,随后断面面积增大,流速V又减小,然后水流流速就会重复这样的周期进行变化,这便是每一个鱼池流速波动的原因。
另外,由于鱼道不是绝对光滑,会存在沿层阻力系数,会产沿层损失,使得水流的能量减小,再加上水流撞击在异侧竖缝上面,会产生局部损失,水流的能量也会减小。两者均为能量损失,使得总水流的能量为损失,所以相对上一级水流的最大速度有所减小。因此,每一个鱼池的最大流速相对于上一个鱼池的最大流速稍有减小。

Table 1. The velocity data of fishway
表1. 鱼道沿程流速数据
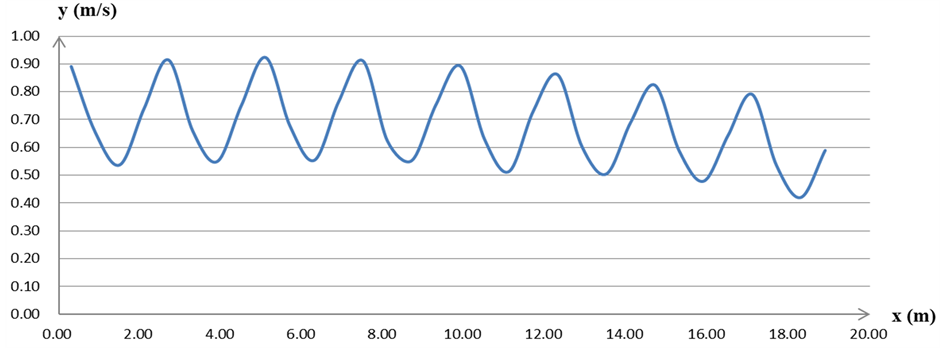
Figure 2. Schematic diagram of velocity variation
图2. 各鱼池沿程流速变化示意图
4.2. 第三级鱼池的流速测量结果
根据Wu等人 [5] 的研究,对于鱼道的大部分鱼池而言,其中的水流流态基本一致,同时,当鱼道坡度小于10%时,鱼池中水流呈明显的二维特征,因此本实验(鱼道坡度为6%)只取二维结果,另外,由于篇幅原因,这里只列出了第三级鱼池的试验数据。
表3的数据是表2中每个横坐标所对应的最大流速,11个点,如图3所示。由图3及表3可以看出,

Table 2. Velocity data of the third pool
表2. 第三级鱼池的流速数据

Table 3. Velocity data of the mainstream
表3. 第三级鱼池同一列最大流速表
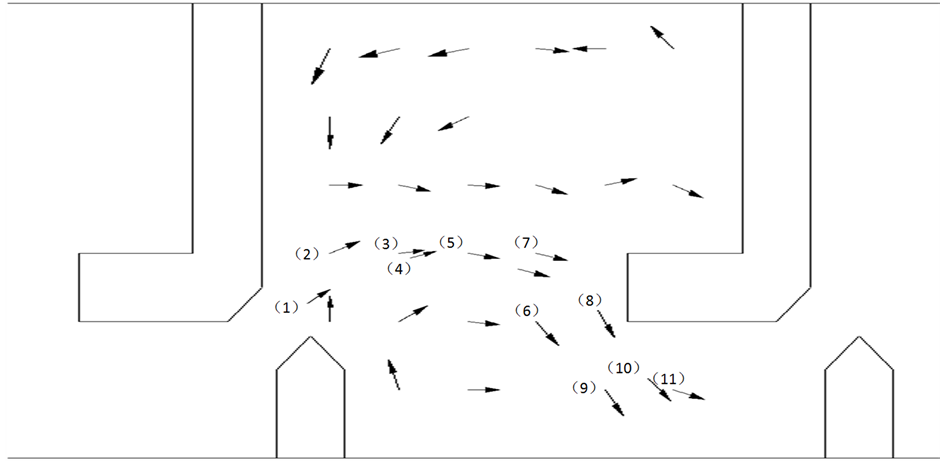
Figure 3. Velocity diagram of the third pool
图3. 第三级鱼池流速示意图
每一级鱼池中,最大的流速出现在竖缝附近处,在一个鱼池中主流流速前部分沿程有所减小,后部分又有所增大。随着水流向鱼池中间段流去,主流的路径会越来越靠近鱼池中央,然后又会偏向下一个竖缝处,鱼池流态大致形状为一个“S”型。
另外,水流流速在主流处向鱼道两侧呈一个衰减趋势,但是当要靠近鱼池两侧时,水流流速又有所回升。同时,在主流两侧均有水流的回流,在每个鱼池中形成2个回流区,其流速较小,可作为洄游鱼类的休息区域。
5. 结论
(1) 通过对竖缝式鱼道的模型试验研究,本文可得出以下几点结论:
(2) 竖缝式鱼道整体主流流速沿程一直处于波动状态,以一个鱼池为一个周期变化。
(3) 竖缝式鱼道整体主流流速每一个周期较前一个周期的最大主流流速有所减小。
(4) 竖缝式鱼道在每一级鱼池的主流流速沿程变化表现为:在前半池长,主流流速逐渐减小;在后半池长,主流流速逐渐增加,主流流速最大在竖缝附近。
(5) 竖缝式鱼道在每一级鱼池会形成2个可供鱼休息的回流区域。
基金项目
四川省教育厅(2017-1399);四川农业大学(03571673, 04051812, 04054586)。