1. 引言
近年来,电网快速发展,电网基建、电源送出、电网改造项目大量投产,导致电网规模不断增大。同时为响应国网号召的一体化建设,各级调度的电网模型拼成一张大网,在全网统一模式下整定计算时,面对的是全模型,模型节点数目极其庞大。另外,随着智能电网建设带来的网络重构,电网非正常运行方式明显增多,且方式间组合灵活,导致全网模型计算复杂,计算效率降低。所以对整定计算效率提出了新的挑战。
目前,对于整定计算的模型通常采用两种模型:分区和不分区。基于全网不分区计算,选择的是全网的计算模型,当矩阵规模增大时,耗时成指数增加。甚至当电网电气节点数增加到一定数量,会导致计算机内存溢出,无法计算的情况。分区计算是指在整定计算的时候选择计算区域的所有与其他区域的等值,因为其他区域是以等值的形式参与计算,所以无法查看故障后其他区域信息、无法考虑其他区域的检修和无法考虑其他区域的厂站方式。
为了解决上述问题,本文提出了基于自适应算法的电网动态分区。根据边界支路、运行方式实时调节,选择合适的配合区域及约束区域,最终确认整定计算的最终计算模型。
2. 整定计算数学模型
2.1. 边界支路的判断
厂站区域的划分的思想是将全网模型中的线路按照指定的准则把其中的某些线路打断,从而把原全网模型区域“切割”成若干个独立的子区域,这些被打断的线路的权值之和被称为边界支路。
首先为线路增加首末母线和首末厂站的属性,设置其中一侧的母线为线路的首母线,那么对应的对侧的厂站就是线路末母线。定义首母线所在的厂站为线路的首厂站,末母线所在的厂站为末厂站。
对于一条线路来说,如果其首厂站和末厂站是同一厂站那么可称为站内线路;相反的,首厂站和末厂站是不同厂站那么为站间线路。对于站内线路,线路的两侧所在的厂站一样,这个在分区的时候不考虑;对于站间线路,线路的两侧厂站所在区域不一样,那么我们在划分区域的时候,可以直接给厂站划分区域,那么如果一条线路两侧的厂站属于不同的区域,那么这条线路就是需要被打断的线路,也就是边界支路。
2.2. 整定计算数学模型
以全网作为研究模型,以厂站作为最小的结点。即当厂站分区完成后,该厂站内的所有元件都在对应的区域内 [1] [2] 。
对于任意电网,可以将厂站按照地理位置或是所属调度分成若干个区域,分区后电网模型如图1所示。因为电网是互连的,所以区域之间一定是有联系的。在整定计算时保留计算区域的全部模型和边界
线路以及边界母线,并将其他区域以等值的形式参与计算,从而保证计算的正确性。
区域A的网络参数、区域A、B、C之间的连接支路、区域B、C在边界母线的等值,从而形成一个与原始网络等值且矩阵阶数大大减少的网络。
由于在整定计算时选用节点阻抗矩阵,设大型互联电网包括k个区域电网,每个区域电网包括n个节点,则各区域电网序网阻抗矩阵存储规模的总和为kn2,如果不考虑在各区域中重复出现的边界节点数,则互联电网的节点数为kn,从而其序网阻抗矩阵的存储规模为k2n2,显然,区域电网越多,按区域电网组织数据的方式其在阻抗矩阵存储规模方面的优越性越大。由于分成了小网络,这样既真实的反映了全网,保证了计算的正确性,又大大缩小了研究模型的规模,极大提高了运算速度。但是又不能无限的增加分区数,当区域数增大时,计算各区域的等值的耗时增加,而且分区受模型的影响,当两个厂站联系比较紧密的时候,分成两个区域等值较多,影响计算正确性。
2.3. 目标函数
如何能够保证在分区后区域间连接线最少,区域的规模和区域数满足要求是动态分区所要解决问题。
动态分区的目标是要保证在分区的时候,边界线最少。因而本文以最少的边界支路为目标函数,如下式所示:
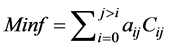 (1)
(1)
其中:Cij为区域i和区域j的边界线,0为未连接;其他为边界线数;aij为区域i和区域j之间的加权,根据实际情况设置。
2.4. 附加条件
· 在实际应用过程中,根据故障点位置为区域中心,生成的计算区域,主要考虑如下附加条件:
· 在模拟发生故障时,需要查看附近几级范围内电网的故障后信息,所以要以故障点为中心,N级范围的设备都在计算区域;
· 在计算整定参数时,保证配合支路能够和整定支路同一区域内;同时考虑检修方式时,保证检修的支路也和整定支路在计算区域。
· 等值发布也需考虑等值点附近几级的检修情况,也需保证检修设备在计算区域。
· 为了保证计算的正确性,互感的两条支路要在一个区域内。
2.5. 终止条件
区域中的厂站数过大或过小直接影响厂站分区效果及计算效率,区域厂站数过大会导致分区的意义减小,而无限制的减少子区域厂站个数会导致区域数目的增加,降低分区效率。所以增加区域数和每个区域规模两个约束。
为了保证分区后区域规模和区域数合理,使用如下约束条件:
· 分成完成后,一共分成的最大区域数;
· 分区后的每个区域最大厂站数;
根据分区终止条件,绘制分区流程图如图2所示。
第一步,根据附加条件给电网进行初始的分区,合并互感支路区域,将计算支路、配合支路的区域合并,作为初始的分区模型。
第二步,重新计算区域数,判断是否满足分区终止条件,若满足,分区完成,若不满足,继续分区,直到满足分区完成条件,分区完成。
3. 基于遗传算法的动态分区模型
3.1. 遗传算法
遗传算法 [3] - [10] 是一种源于生物界自然选择和自然遗传机理的并行优化搜索方法,它在搜索过程中自动获取和积累对解空间的认识,并自适应的控制搜索过程以求得最优解,但遗传算法在求解问题时存

Figure 2. The flow chart of the partition
图2. 分区流程图
在收敛速度慢的问题。因此,本文提出了改进遗传算法,通过在线自适应调整各种群的交叉率和变异率,提高遗传算法的迭代速度。基于遗传算法整定计算是指整定计算模型根据边界支路、运行方式实时调节,选择合适的配合区域及约束区域,使得边界支路的整定参数是基于最恶劣的运行方式计算出来的,利于获得更精确的整定定值,提高继电保护系统的选择性、速动性、可靠性和灵敏性。
3.2. 染色体编码
将寻优问题代入遗传算法,所要解决的最主要问题是将问题的解与遗传算法中的染色体进行匹配,即一条染色体表示唯一解。
对于动态分区,我们关心的是最终需要查看的信息在计算区域内,边界线最少,区域数和每个区域厂站数合理。以各区域之间的边界支路为染色体编码,若两个区域之间有边界线,那么记录如图3。
如图2所示,每一个基因位表示两个区域之间有的一条边界线联系,这样就可以通过染色体确认分区后的边界支路数以及区域数。
以某一部分电网为例,如图4所示。
如图3所示为厂站的数据模型,表示各厂站间的拓扑连接关系,每个厂站作为一个区域对应唯一节点号。首先,对所有区域进行编号,编号结果如图所示,区域之间的拓扑关系由连接关系确定。如节点号为1的区域对应的连接关系为(1,2)和(1,3),则表示节点号为1的区域和节点号为2的区域之间有一条线路连接,节点号为1的区域和节点号为3的区域之间存在一条线路。同样对于存在互感关系的线路也由区域的节点号表示,在根据条件初始化的时候优先合并。
如表1所示为厂站的数据模型,表示各厂站间的拓扑连接关系,每个厂站作为一个起始区域对应唯一节点号。首先,对所有区域进行编号,编号结果如表1中区域的节点号列,区域之间的拓扑关系由连接关系列确定。如表1中节点号为1的区域对应的连接关系为2@1和3@1,则表示节点号为1的区域和节点号为2的区域之间有一条线路连接,节点号为1的区域和节点号为3的区域之间存在一条线路。同样对于存在互感关系的线路也由区域的节点号表示,表示形式为互感支路1@互感支路2,如表2所示。
互感支路由首末区域的节点号表示,如线路L12与线路L15之间存在互感,则表示为(8,9)@(8,10)。
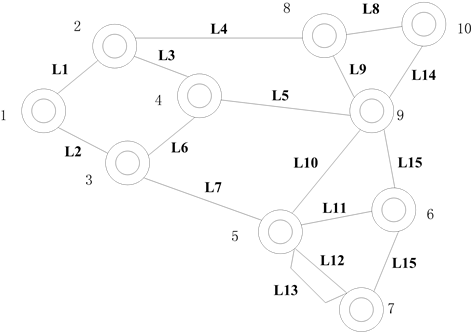
Figure 4. The connection diagram of Station
图4. 示例厂站连接关系图

Table 1. The relationship of Station
表1. 示例厂站连接关系

Table 2. The mutualinductance information
表2. 互感信息
然后根据表1和表2给出加权值。
3.3. 寻优
当为每一个区域染色体编码完成后,我们可以很容易可以获得任意两个区域之间的边界线数。边界线数表明两个区域之间的连接的紧密程度,边界线越多说明两个区域之间连接越紧密。本着尽量减少边界线和保证电网计算准确性的原则,就要先将联系紧密的两个区域合并,若两个区域合并,那么原来两个区域之间的边界线将不再是边界线(因为合并为同一个区域),区域数减一。重新为染色体编码、计算边界线、合并联系紧密的区域。
为了优化分区效率,在合并区域的时候,每次合并多个区域。可以计算出平均边界线数(所有边界线和区域数的比值),当两个区域之间的边界线数大于平均边界线数时,合并这两个区域,这样可以对合并区域效率进行优化,从而得出最终的解决方案。
以矩阵的形式表示,行列为区域的节点号。
· aijCij为区域i和区域j之间的边界支路数值,其中互感的加权值取100,区域i和区域j最终的边界支路数值为根据连接关系求得的边界支路数值与加权的和。
· 求出所有区域之间aijCij的平均值为32.3,然后把大于aijCij的平均值的区域合并,即合并区域8、区域9、区域10为一个新区域,区域2、区域3、区域4为一个新区域;
· 合并后的区域如图3所示,判断是否满足分区终止条件。因为举例的电网模型较小,将每一个厂站作为一个区域,若图2每一个初始区域为已经聚集了N次后的区域的集合,那么此时可能满足终止条件,分为6个区域。若仍不满足,则重新计算新区域之间的Minf值。
4. 算法的具体实现
以流程化故障计算为例对算法实现流程进行说明,见图5:
1. 以各厂站为一个子区域,开始分区;
2. 根据目标函数,计算边界支路数;
3. 根据初始条件初始化模型;
4. 计算各区域之间的边界数,已经所有边界数;
5. 计算出所有基于所有边界数的平均边界数;
6. 将区域之间边界线数大于平均边界数的区域合并;
7. 重新计算区域间边界线数;
8. 区域合并,计算区域数和每个区域的厂站数是否满足终止条件;
9. 若不满足,合并边界支路最多的两个子区域。
重复3~6步,若满足,则分区完成。
约束条件的考虑因素:
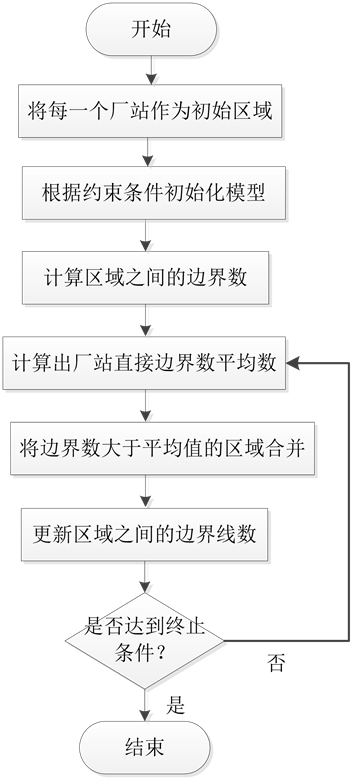
Figure 5. The connection diagram of genetic algorithm
图5. 基于遗传算法流程图
1. 查找全网范围内的互感支路,将同一组互感支路关联区域合并;
2. 根据故障位置确定计算区域,认为故障位置所在的区域为故障计算区域;
3. 将配合支路加到计算区域内;
4. 将附近3级以内的厂站增加到计算区域;
5. 将环网结构和厂站范围增加到计算区域;
6. 约束条件后模型完成。
5. 算例分析
采用示例电网对本文提出的基于遗传算法动态分区进行验证。此示例电网包含4642条支路,2960个厂站。收集电网中所有支路互感信息,设置互感支路的加权值(可设定为100),初始模型建模完成。
采用本文算法对示例电网拼接后的模型进行优化。终止条件为:区域数达到5个,单个区域厂站数达到1500,具体信息见图6和图7。
由算例可以看出:
1. 在分区开始时,由于采用了优化算法,生成的区域数成指数下降,分区效率很高;
2. 分区完成后,各区域的节点数在1500左右,区域规模相差不大,分区合理。
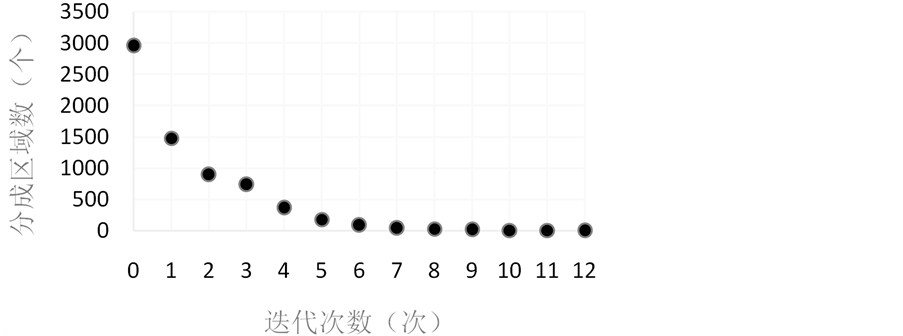
Figure 6. The relationship between iterations and matrix
图6. 迭代次数和分成矩阵数的关系
6. 结论
文章针对目前电网规模和运行方式增加影响整定计算效率这个问题,提出了基于遗传算法的电网动态分区算法,首先深入研究电网的模型特点,抽象出电网数学模型,然后给出遗传算法的目标函数及约束条件,同时在分区的时候对算法进行了优化,增加了分区效率,算例仿真表明了该算法的有效性和实用性。