1. 引言
上世纪八十年代出现了世界上第一种双自由度齿轮传动机构—Trallfa球齿轮，但该齿轮加工难度大、承载能力低，精度不高，并没有得到推广应用 [1] 。九十年代国防科技大学潘存云教授发明了一种新型的双自由度齿轮传动机构—渐开线球齿轮机构，克服了离散齿球齿轮存在的传动原理误差和难以加工的缺陷 [2] 。球齿轮齿盘传动传动是球齿轮传动的一种特殊形式，与齿条传动类似。该机构可以实现球面运动和平动之间的相互转换，迄今为止还没有其他机构能实现该运动形式。球齿轮齿盘机构的运动规律符合喷泉机的运动特性，本文将该机构应用在喷泉机上，设计出漂亮的水花，供人们的观赏。
目前，对球齿轮传动的相关研究主要集中于球齿轮的曲面方程的推导、运动分析、传动理论及接触分析、加工原理、加工方法以及装配误差 [3] 。潘存云教授对球齿轮啮合原理、杰出特性等进行了系统介绍，并对其运动规律进行深入分析。首先提出一种可实现精确运动的球齿轮传动机构——三自由度机器人柔性手腕机构，并提出三种比较简单的加工球齿轮方法：仿形法车削加工、仿形法铣削加工和范成法车削加工,为球齿轮的加工奠定了基础 [4] 。建立了新型球齿轮齿廓曲面的参数方程，推导了球齿轮机构中齿轮的环形齿面方程、啮合方程以及共轭齿廓曲面方程 [5] 。姚其水教授等对潘存云关于球齿轮的参数方程进行简化和补充，方便了建模过程 [6] 。目前球齿轮传动设计的定向平台能够应用在定向、导航、适量推进、轮腿复合机器人等系统中，在航空航天、武器研制、机器人等领域具有广阔的应用前景 [7] 。
球齿轮齿盘机构的传动形式比较简单，只需要对齿盘进行两个方向的输入，就可以输出相应的球齿轮的转动，且输出轴负载小，有利于提高其动态性能 [8] 。喷泉机的喷头部分运行速度不高，可以考虑用PLC控制电机，进而驱动齿盘运动，从而带动球齿轮及其喷头做各种不同轨迹的运动。喷头大致分为直流喷头、涌泉喷头、集束喷头和旋转喷头等，喷出的水形各异 [9] 。根据设计要求，可以在球齿轮末端加装各种喷头，同时喷出不同的水花。
本论文通过SolidWorks建模、ADAMS仿真，以研究其运动形式和规律 [10] 。在仿真环境中对球齿轮输入设定的轨迹，来观察齿盘的运动规律；然后将齿盘的运动参数转化为电机的转动参数，最后用PLC进行编程，控制喷泉机的喷头按照设定轨迹运动。
2. 喷泉机原理分析
2.1. 渐开线球齿轮形成原理
渐开线球齿轮齿面的形成原理可用图1予以说明。C为基圆，K-K为发生线，N、S为基圆与旋转轴的两个交点，发生线K-K与旋转轴始终在基圆平面P内。当发生线K-K在基圆上作纯滚动，并随基圆平面P一起绕旋转轴作回转运动时，发生线上任一点的轨迹便形成了球齿轮的齿面，基圆上所有点的轨迹的集合称为基球。显然，在过旋转轴的任意剖面内的齿廓曲线均为渐开线，所有渐开线的集合构
Figure 1. The generation of the involute spherical gear
图1. 渐开线球齿轮齿面的生成
成为一个环状曲面。极轴端部的球齿轮为一柱状回转体的球形齿轮为中凸齿轮，极轴端部为一回转凹坑的球形齿轮为中凹齿轮。
当其中一个球齿轮的齿数为无穷多时，其分度球半径亦将趋于无穷大，则球齿轮演变成齿盘，球齿轮机构演变成球齿轮齿盘机构。其中球齿轮做球面运动，齿盘做平面运动，如图2所示。
2.2. 喷泉机驱动机构分析
图3所示为喷泉机驱动部分的实物图，以圆环中心为原点建立空间直角坐标系。1为X向上的驱动电机1，2为Z向上的驱动电机2，3为喷泉机的底座。4为滑块a，5滑块b，滑块b在滑块a上沿Z轴运动，滑块a在底座上沿X轴运动。6位支架，7为圆环，8为球齿轮，9位齿盘。圆环与支架铰接，球齿轮通过横轴与圆环铰接，球齿轮可以在空间内做两自由度的转动，且转动中心位于圆环的中心位置。齿盘与球齿轮啮合，且齿盘通过螺丝固连在滑块b上，齿盘随滑块b在XOZ平面内做两自由度的平动。球齿轮顶部可以根据设计加装不同类型、不同数目的喷头，跟随球齿轮一起转动。
电机1、2驱动滑块带动齿盘与球齿轮啮合运动，将齿盘的平动转化成球齿轮的转动。给电机1、2输入给定的参数，使得球齿轮带动喷头按照设计的轨迹运动，从而使喷头喷出不同轨迹的水形。
2.3. 喷泉机控制原理分析
喷泉机运行速度不高，但对运动精度要求较高，采用PLC控制步进电机的方式来控制喷泉机的运动。步进电机试讲电脉冲信号转变为角位移或者线位移的开环控制元件，在正常运转情况下，步进电机的转速和角位移仅取决于脉冲信号的频率和脉冲数，而不受负载的影响。即给步进电机一个脉冲信号，电机相应的转过一个步距角。通过KGLWIN软件对PLC进行编程，对步进电机输入给定的脉冲信号频率和脉冲数，从而输出需要的电机转速和角位移，实现球齿轮带动喷头按照设计的轨迹运动。图4为控制流程图。
3. 喷泉机运动学模型
建立如图3所示的固定坐标系[O,X,Y,Z]，O为球齿轮转动中心，在球齿轮转动过程中，O的坐标始终不变。定义球齿轮极轴的末端中心点为P，OP长度为 ；球齿轮中间齿的中心点为Q，OQ长度为 ；齿盘中间齿中心点为M。定义球齿轮极轴与OY轴的夹角为偏转角 ，规定偏离初始位置转动为正，反之为负；极轴在XOZ平面内的投影与0Z轴正方向的夹角为方位角 ，规定逆时针转动为正，反之为负。初始状态下θ = 0，α = 0，极轴与XOZ平面垂直；运动时
，
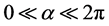，极轴的运动范围限定在一个圆锥内，且啮合传动过程中存在约束关系：
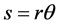(1)
式中：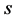
表示齿盘位移，
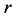表示OQ长度，即球齿轮节球半径。
Figure 2. 3-D solid model of the involute spherical gear and ring rack
图2. 球齿轮齿盘机构三维模型图
Figure 3. Picture of real product of the fountain’s driving part
图3. 喷泉机驱动部分实体图
为了方便分析，可以理解在球齿轮和齿盘啮合的每一个瞬间，为齿轮与齿条的啮合。球齿轮有两个方向的转动自由度，齿盘有两个方向的平动自由度，球齿轮齿盘机构就具有四个独立自由度。根据自由度计算公式可得该机构的自由度为2，原动件也为2，因此该机构具有确定的运动。在此规定：已知齿盘的位移
、
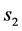，求解球齿轮极轴的相关参数的过程为正运动求解；已知球齿轮极轴的偏摆角和方位角，求解齿盘的相关参数的过程为逆运动求解。
3.1. 正向运动模型
如图5所示，P’为P点在XOZ平面的投影。给定齿盘位移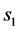
、
，可以求出对应的方位角α和偏转角θ。
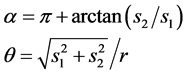(2)
式中：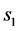
表示Z轴位移，
表示X轴位移。
已知OP长度L = 15 mm，可求出P点坐标：
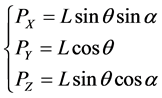(3)
、
、
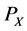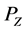分别表示P点在X、Y、Z轴上的坐标。
3.2. 逆向运动模型
给定球齿轮末端P点的偏转角和方位角，如图5所示，可以根据式(1)、式(2)反求齿盘的位移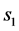
、
：
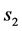(4)
θ表示偏转角，α表示方位角，r表示球齿轮节球半径。
、
确定以后，就可以推算出驱动电机的转动参数，然后输入PLC中进行控制，就可以让喷泉机按照设定的轨迹运动。
4. 喷泉机驱动机构建模
渐开线球齿轮以及齿盘在ADAMS的数据库里没有标准件，直接制作比较困难，因此先通过SOLIDWORKS软件生成各个零部件后进行装配，然后导入到ADAMS中。
4.1. SolidWorks生成零部件
第一步生成球齿轮。从设计库的TOOLBOX选取Gb、动力传动、正齿轮，设置具体参数，生成极薄的标准正齿轮。选取其中连续7个齿进行拉伸切除，然后截取轮齿部分再进行拉伸切除。在第4个齿的中间标示中心线，以中心线为轴进行旋转拉伸，然后在末端圆面再进行拉伸，生成球齿轮三维模型图，如图6所示。
第二步生成齿盘。从设计库的TOOLBOX选取Gb、动力传动、齿条，设置具体参数，生成极薄的标准齿条。选取其中连续6个齿进行拉伸切除，在第3个齿和第4个齿的中间位置标示中心线，以中心线为轴旋转生成齿盘三维模型图，如图7所示。
第三步依次生成其他零部件：支架、圆环、滑块、底座等。
Figure 6. 3-D solid model of the involute sphe- rical gear
图6. 球齿轮三维模型图
Figure 7. 3-D solid model of the ring back
图7. 齿盘三维模型图
4.2. ADAMS添加约束
将SolidWorks生成的零件保存为Parasolid格式，然后导入到ADAMS中。然后对零部件进行连接，添加相应约束关系：底座与大地是固定副连接，滑块a与底座是移动副连接，滑块b与滑块a是移动副连接，球齿轮和齿盘是接触力连接，球齿轮和圆环是旋转副连接，圆环和机架是旋转福连接，机架和大地是固定副连接。
5. 仿真分析
通过设计球齿轮末端P点的轨迹，然后将运动参数输入ADAMS仿真环境进行仿真，可以得出齿盘运动规律，继而求出电机的变化规律，然后用PLC进行编程控制。
5.1. P点做圆周运动
z设计球齿轮的运动轨迹为：球齿轮极轴沿X正向偏转30˚，然后绕OY轴顺时针转动一周。其中步骤①运行1 s，步骤②运行6 s，运动轨迹如图8所示：
用ADAMS输入P点的运动轨迹，采用一般驱动进行仿真运动，可以得到M点在X轴、Z轴坐标。在ADAMS中对P点的X、Z向位移分别编程：
X—if(time-1:15*sin(30d*time),15*sin(30d*time),15*sin(30d)*cos(60d*(time-1)))
Z—if(time-1:0,0,15*sin(30d)*sin(60d*(time-1)))
将仿真结果与理论计算的结果进行对比，如图9、图10所示。其中图9表示M点在Z轴方向上的仿真结果与理论结果，蓝色的是理论值，红色的是仿真值；图10表示的是M点在X轴方向上的仿真结果和理论结果,蓝色的是理论值，红色的是仿真值。
5.2. P点做螺旋上升运动
设计球齿轮的运动轨迹为：球齿轮极轴沿X轴正向偏转10˚，然后绕OY轴顺时针转动两周，同时P点沿Y轴正方向上做匀速直线运动，最后回到原点。步骤①运行1 s，步骤②运行24 s。P点运动轨迹如图11所示：
在ADAMS中对P点的X、Z向位移分别编程：
X—if(time-1:15*sin(10d*time),15*sin(10d*time),sin(10d)*(15-15*cos(10d)-15*(1-cos(10d))*(time-1)/24)*cos(30d*(time-1))/(1-cos(10d)))
Z—if(time-1:0,0,sin(10d)*(15-15*cos(10d)-15*(1-cos(10d))*(time-1)/24)*sin(30d*(time-1))/(1-cos(10d)))
将仿真结果与理论计算的结果进行对比，如图12、图13所示。其中图12表示M点在Z轴方向上的仿真结果与理论结果，蓝色的是理论值，红色的是仿真值；图13表示的是M点在X轴方向上的仿真结果和理论结果，蓝色的是理论值，红色的是仿真值。
5.3. 结果分析
图式表明，M点的理论值与仿真值误差极小，因此本文所建立的模型是有效的，产生误差的原因是在ADAMS的装配过程中产生了误差。基于本文的模型，在后续的工作中可以在球齿轮顶部加装喷头装置，然后考虑水的重力、空气阻力、出水口处水的压力以及速度等因素，设计出不同轨迹的喷泉。
6. 结论
1) 提出了一种基于球齿轮齿盘传动的新型喷泉机，建立了喷泉机的运动学模型。
2) 求出了球齿轮齿盘机构的运动规律，通过ADAMS仿真实验，验证了模型的有效性，为控制喷泉运动提供了理论基础。
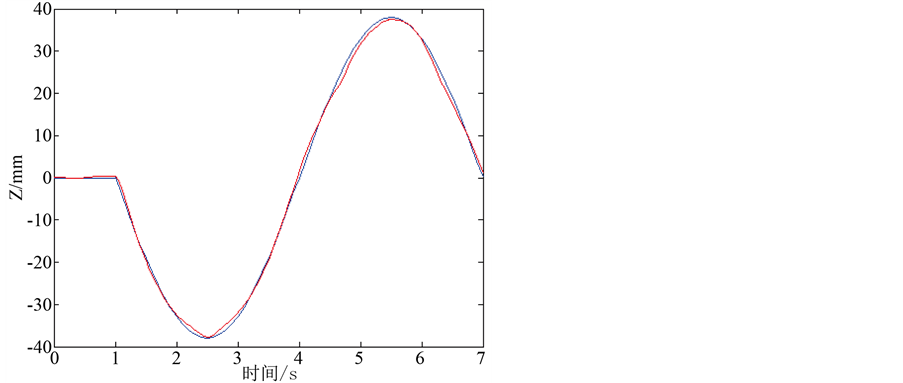
Figure 9. Theoretical value curves and simulation values of po- int M on Z axis
图9. M点在Z轴理论值与仿真值变化曲线
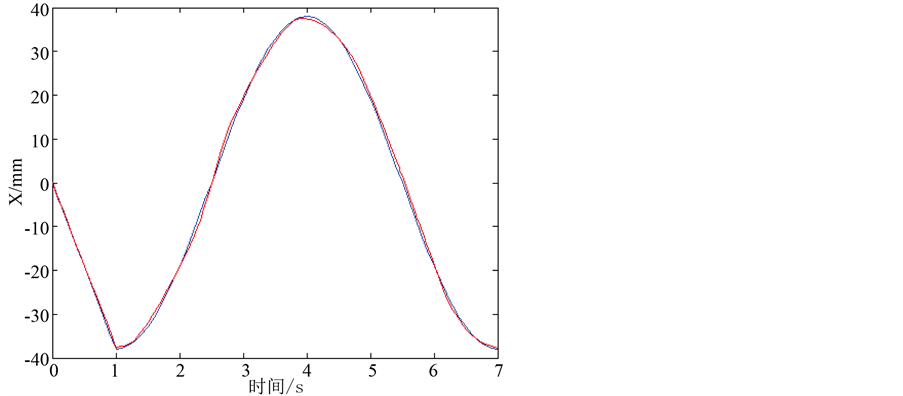
Figure 10. Theoretical value curves and simulation values of point M on X axis
图10. M点在X轴理论值与仿真值变化曲线
Figure 12. Theoretical value curves and simulation values of point M on Z axis
图12. M点在Z轴理论值与仿真值变化曲线
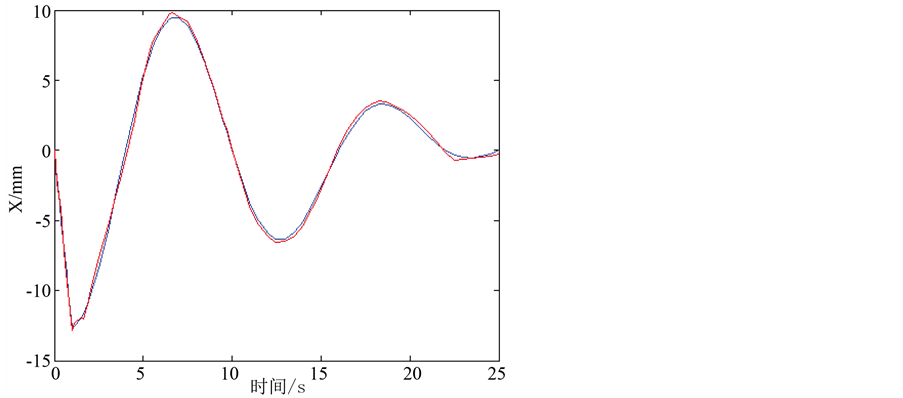
Figure 13. Theoretical value curves and simulation values of point M on X axis
图13. M点在X轴理论值与仿真值变化曲线
3) 结合喷泉机实物的相关参数，对喷头轨迹进行设计，反求出了电机的变化规律，为采用PLC控制电机驱动喷泉机提供了依据。