1. 引言
机车车辆可以抽象为由车体、构架等主要部件构成的多刚体系统，每个刚体具有六个自由度(伸缩、横摆、浮沉、侧滚、点头、摇头)。
一般地，在车辆振动幅度不大、主要部件对称布置、悬挂系统在线性范围内工作时，车辆的垂向振动和横向振动仅存在弱耦合。由于车辆前后悬挂系统的对称布置，车体和转向架各自的点头振动产生的支反力反向，不会产生垂向合力，车体的和构架的低频浮沉与点头运动也解耦进行独立研究。另外，由于车辆主要部件的弹性体振动频率远大于垂向动力学分析中感兴趣的低频段，在分析时为了简化模型将其视为刚体，且忽略弹簧单元质量、阻尼单元质量、轮轨间的微小弹性振动。
在此基础上本文建立了两自由度有阻尼强迫振动模型，建立车辆系统在振动激励下的动力学微分方程，并求解得到构架和车体的振幅表达式。最后基于Simpack多体动力学软件，建立了动车组的非线性多体动力学仿真模型，分析了不同垂向悬挂阻尼对车体振动幅值的衰减情况 [1] [2] [3] 。
2. 机车车辆垂向自由振动模型及振型分析
为了分析车辆系统垂向振动模态，建立机车车辆两自由度无阻尼自由振动模型如图1(a)所示。
其中：m1为整车转向架构架质量，m2为车体质量，x1为转向架浮沉位移，x2为车体浮沉位移，k1为整车一系悬挂垂向刚度，k2为整车二系悬挂垂向刚度。
根据牛顿–欧拉公式，得到车体与构架浮沉自由振动微分方程如式(1)所示。
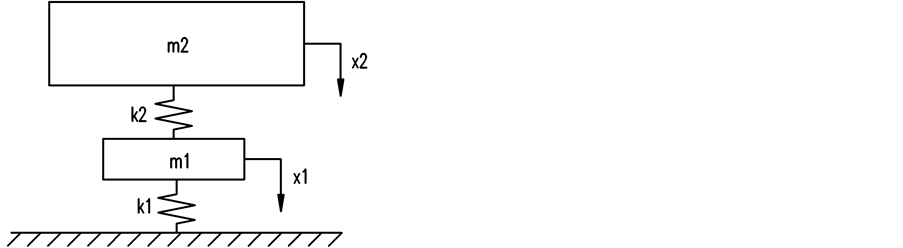
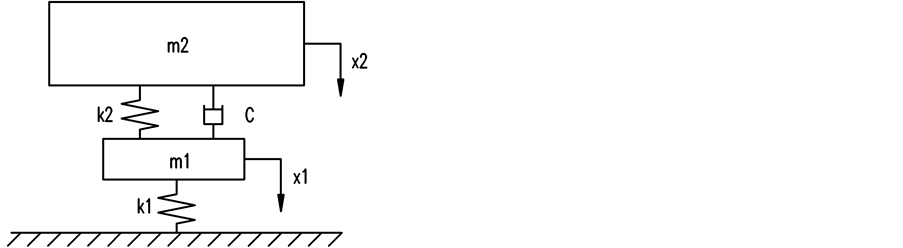(a) 无阻尼 (b) 有阻尼
Figure 1. Tow-DOF vibration model of vehicle
图1. 机车车辆两自由度振动模型
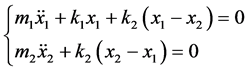(1)
设方程的解为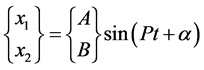
，代入式(1)，求解得到系统方程的特征值为
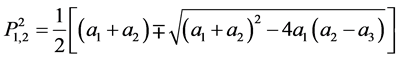
其中方程的特征值P1、P2分别为两自由度振动系统低频、高频自振角频率。两自由度系统的两种振型如下：
低频振型：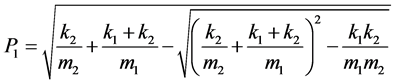
，
，
；
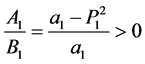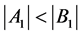高频振型：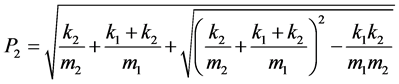
，
，
。
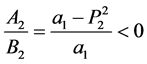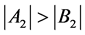综上所述，车辆的低频固有振动表现为构架与车体的同向振动，且车体的振幅较大；车辆的高频固有振动表现为构架与车体的反向振动，且转向架构架的振幅较大 [2] 。
3. 机车车辆垂向有阻尼振动模型及振动传递分析
为了研究车辆系统在轨道振动激励下的振动传递情况，假设转向架受到线路周期性位移激励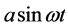
。另外，为了衰减振动，悬挂系统中多在二系中设置阻尼单元，如图1(b)所示，包括二系垂向减振器(例如CRH3型动车组车辆、部分铁路客车车辆)、带有节流孔的空气弹簧(例如CRH2型动车组车辆)。动车组客车通常在一系也安装垂向减振器，但由于二系浮沉振动幅值远大于一系，一系垂向减振器主要用于衰减点头振动，而车体浮沉振动的能量主要由二系阻尼单元来衰减。因此在分析车辆的浮沉振动时为了简化模型，忽略一系阻尼单元 [4] [5] 。
因此，则根据式(1)得到两自由度有阻尼受迫振动微分方程如下：
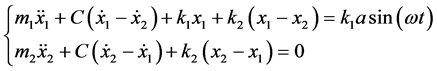(2)
方程(2)解的形式为：
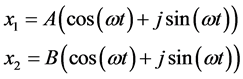
A、B分别表示构架与车体的振幅，解得：
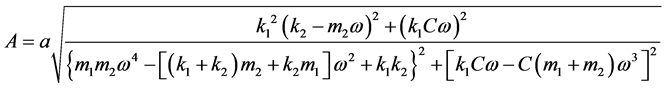
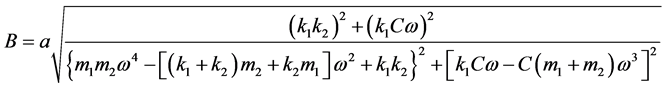
4. 机车车辆二系垂向阻尼对车体振动幅值衰减的影响
以某动车组车辆为例，基于Simpack多体动力学软件，考虑了非线性的轮轨接触几何关系、非线性
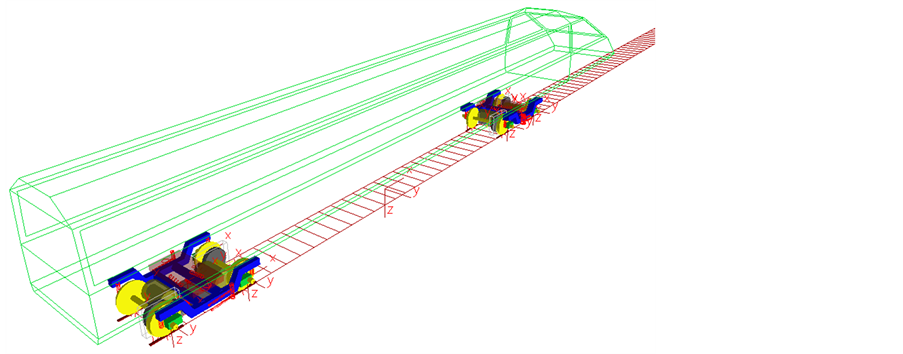
Figure 2. Simulation model of vehicle system
图2. 车辆多体动力学仿真模型
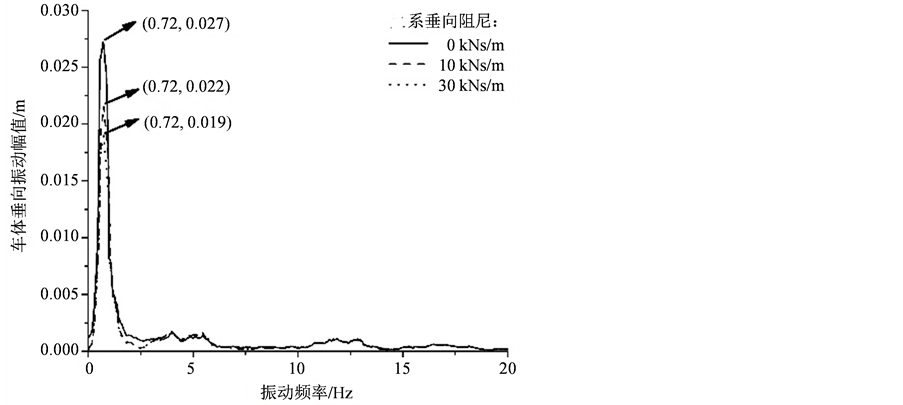
Figure 3. The amplitude-frequency characteristic of carbody with different vertical damper
图3. 不同垂向阻尼下车体垂向振动幅频特性
的轮轨相互作用力和非线性的悬挂参数等非线性环节建立车辆系统多体动力学仿真模型。车体、构架和轮对考虑了六个方向上的自由度，即纵向、横向、垂向、侧滚、点头和摇头，转臂具有点头自由度，车辆系统共有50个自由度。基于Simpack的车辆多体动力学仿真模型如图2所示。
施加武广随机轨道谱，进行多体动力学仿真，得到不同二系垂向阻尼(0 kNs/m、10 kNs/m、30 kNs/m)下车体垂向振动的时域信号 [6] 。通过傅里叶变换得到车体在上述工况下的振动幅频特性，如图3所示。
通过图3可知：车体的垂向振动能量集中在低阶自振频率(即P1)附近；通过设置二系垂向阻尼，可以明显衰减车体自振频率下的振幅。
5. 结论
本文通过理论计算，得到了车辆两自由度系统振动模态以及车体和构架的振幅表达式，分析可知：车辆的低频固有振动表现为构架与车体的同向振动，且车体的振幅较大；车辆的高频固有振动表现为构架与车体的反向振动，且转向架构架的振幅较大。
通过车辆多体动力学仿真计算，得到了车体垂向振动的幅频特性，二系垂向阻尼对于车体的垂向振动幅值具有明显的衰减作用。
基金项目
山东省科技重大专项(2015ZDXX0102A01)——出口型动车组高速转向架技术研究。