1. 引言
铁电材料因具有自发极化、快速响应及低功耗等特性,被广泛应用于各个领域之中,如航空航天、固体制冷及传感技术等。目前,铁电电子器件的尺寸已达到纳米甚至微纳米尺度。随着器件尺寸的不断减小,畴壁结构对器件性能的影响也越发显著,如极化的头-头或尾-尾相接会使铁电材料出现导电性。因此,铁电体畴壁结构对材料性能的影响逐渐成为研究热点 [1] [2] 。
之前一些以块状钛酸钡(BaTiO3, BTO)样品为研究对象的研究忽略了畴壁的独特性能 [3] [4] [5] 。但随着研究的深入,一些研究者开始对铁电畴壁内部结构展开研究,试图通过改变外加条件来定向调控铁电材料畴结构,进而优化铁电材料的性能。Yoshihiro等人 [2] 发现BTO中的力电耦合对铁电畴壁会产生巨大的影响。目前的观点认为铁电材料180˚畴壁是Ising畴壁,它的特点是畴壁内部极化矢量的方向平行于畴壁,且仅仅只存在一个极化分量,如图1(a)所示。当存在力电耦合时,Ising畴壁的极化分量会变得不
 (a) Ising domain wall (b) Left-handed helical domain wall (a) Ising畴壁 (b) 左手螺旋畴壁
(a) Ising domain wall (b) Left-handed helical domain wall (a) Ising畴壁 (b) 左手螺旋畴壁  (c) Right-handed helical domain wall (d) Bichiral domain wall(c) 右手螺旋畴壁 (d) 双手性畴壁
(c) Right-handed helical domain wall (d) Bichiral domain wall(c) 右手螺旋畴壁 (d) 双手性畴壁
Figure 1. The schematic of 180˚ domain wall structures
图1. 180˚畴畴壁结构示意图
稳定,畴壁平面出现另一个极化分量使电中性180˚畴壁出现手性相关的螺旋极化曲线 [6] (Bloch畴壁)。所谓Bloch畴壁是指畴壁内极化矢量的大小不变,极化矢量方向通过顺时针或逆时针旋转形成螺旋结构,如图1(b)、图1(c)所示。有研究者提出了在三角形对称的单畴铁电体中具有两个极化分量的畴壁是非手性的,它的极化在畴壁两边沿着相反的方向翻转,在畴壁中心处极化值为0 [7] [8] ,Houchmandzadeh [9] 课题组把这种畴壁结构叫做“双手性”,所谓的双手性结构是指畴壁两端的极化向量同时翻转,翻转方向相反,且通过畴壁中心的极化值为0。这种电中性180˚双手性畴壁可以由挠曲电(应变与有序参数梯度的双线性耦合)效应产生,与传统的左手或右手Bloch畴壁相比,在空间翻转中不会破坏畴壁的对称性,如图1(d)所示。运用具有双手性结构的铁电材料制备的存储器,可以实现超高密度存储。同时,双手性畴壁的迁移势垒,即畴壁从一个稳态翻转到下一个稳态外界所提供的能量,较Ising畴壁低。因此,具有双手性畴壁的铁电材料在低功耗器件的研究与应用方面有巨大的潜力。
有研究报导称,挠曲电效应使铁电材料180˚畴壁具有双手性结构 [10] ,但没有完整提出外部条件对双手性畴壁的影响。因此,本文以笛卡尔坐标系为参考系,分析不同温度、电场以及梯度系数等因素对电中性BTO 180˚双手性结构畴壁的影响。通过数值计算方法得到BTO的极化值,并绘制双手性畴壁的极化曲线图。以此展开对铁电薄膜畴壁手性的研究,有助于掌握使用外场通过畴壁手性来调控铁电薄膜性能的方法,为铁电薄膜性能优化提供理论指导。
2. 研究方法与手段
2.1. 金兹堡-朗道-德希文理论
考虑铁电材料BTO与母相呈 对称,铁电材料BTO的电位移场为
对称,铁电材料BTO的电位移场为 ,其中
,其中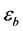 为基底电介常数,E为电场向量,P为极化向量,D满足泊松方程:
为基底电介常数,E为电场向量,P为极化向量,D满足泊松方程:
 (1)
(1)
将铁电极化扩展到六阶,考虑含梯度项、挠曲电项热力学吉布斯自由能写成以下形式 [11] :
 (2)
(2)
其中, 、
、 、
、 、分别为二阶、四阶、六阶介电常数,
、分别为二阶、四阶、六阶介电常数, 为梯度张量,
为梯度张量,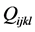 为电致伸缩张量,
为电致伸缩张量, 为柔性张量,
为柔性张量, 为应力张量,
为应力张量, 为挠曲电张量,
为挠曲电张量, 为电场。上述参数的具体表达形式如下:
为电场。上述参数的具体表达形式如下:
 ,
, 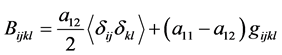 ,
,
 ,
,
 ,
,
 , (3)
, (3)
 为不变张量,当
为不变张量,当 ,
,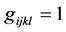 ,否则为0。
,否则为0。 ,
,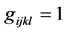 ,否则为0。
,否则为0。
 (4)
(4)
 (5)
(5)
 (6)
(6)
根据热力学和金兹堡-朗道-德希文理论,当吉布斯自由能最低时,铁电材料BTO达到稳定极化值。由吉布斯自由能表达式(2),我们可以获得以下方程:
 (7)
(7)
根据应力平衡状态得到以下方程:
 (8)
(8)
对于吉布斯自由能表达式(2)中的应力梯度,可通过变分来推导应变,应变公式如下:
 (9)
(9)
2.2. 参考系的选定
挠曲电对铁电材料BTO的90˚畴壁与{100}、{110}晶面族的180˚畴壁并无影响。本篇文章选用笛卡尔直角坐标系来描述双手性畴壁,以BTO的电中性180˚双手性结构畴壁作为研究对象,规定铁电极化方向与坐标轴Z方向一致时为正,使用坐标轴中的X方向与畴壁的X2方向的夹角度 来定义畴壁的方位。计算极化时选用的参考系(X1,X2,X3)中的X1,X2平面为畴壁平面,垂直于畴壁平面的X3为演化方向,参考系、畴壁方位以及电中性180˚双手性结构畴壁见上图2、图3所示,图3中的d表示畴壁宽度。
来定义畴壁的方位。计算极化时选用的参考系(X1,X2,X3)中的X1,X2平面为畴壁平面,垂直于畴壁平面的X3为演化方向,参考系、畴壁方位以及电中性180˚双手性结构畴壁见上图2、图3所示,图3中的d表示畴壁宽度。
将铁电材料BTO的相关参数列成表格,如表1所示。其中 表示畴壁翻转前的梯度系数,
表示畴壁翻转前的梯度系数, 表示畴壁翻转后的梯度系数。
表示畴壁翻转后的梯度系数。
2.3. 180˚双手性畴壁能量方程的处理与分析
铁电材料BTO的电中性180˚双手性结构畴壁平行于铁电材料自发极化值Ps的方向,通过求解无应力作用状态下的方程7和方程8,可以得到六个等效的极化状态。考虑极化向量仅在X3方向变化情况,应力张量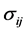 也只与垂直畴壁平面的X3方向有关,且
也只与垂直畴壁平面的X3方向有关,且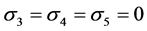 ,在忽略退极化场的情况下,在挠曲电的作用下极化分量只有Ising畴壁的极化P1与Bloch畴壁的极化P2。在新的参考系中吉布斯自由能式(2)可写成以下形式:
,在忽略退极化场的情况下,在挠曲电的作用下极化分量只有Ising畴壁的极化P1与Bloch畴壁的极化P2。在新的参考系中吉布斯自由能式(2)可写成以下形式:
 (10)
(10)
P1与角度 独立,挠曲电作用使畴发生翻转一定角度,Ising畴壁变得不稳定,需要新的极化分量P2来平衡。因此及计算P2时需要对相关参数进行修正,修正公式如下:
独立,挠曲电作用使畴发生翻转一定角度,Ising畴壁变得不稳定,需要新的极化分量P2来平衡。因此及计算P2时需要对相关参数进行修正,修正公式如下:
 (11)
(11)
 (12)
(12)
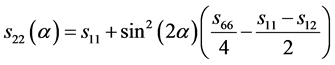 (13)
(13)
 (14)
(14)
 ,
, (15)
(15)
 (16)
(16)
在热力学中,当能量最低时材料处于稳定状态。因此由公式(10)可以得到在X3方向的极化分量P1、P2的表达式。如下公式:

Figure 2. Orientation of the 180˚ domain wall and reference frames used
图2. 180˚畴壁与参考系的方位示意图

Figure 3. P1, P2 profiles of 180˚ bichral domain wall
图3. 180˚双手性畴壁结构P1,P2极化曲线

Table 1. Free energy coefficient of bulk ferroelectric BaTiO3
表1. 块状铁电BaTiO3自由能量系数
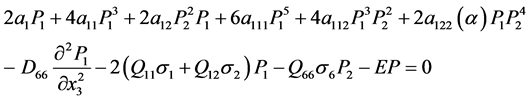 (17a)
(17a)
 (17b)
(17b)
远离畴壁中心的极化边界值为
 (18)
(18)
弹性应力自由的表达式
 (19)
(19)
弹性问题在一维求解的情况下,方程(9)非零弹性应力分量的表达式如下 [10] :
 (20a)
(20a)
 (20b)
(20b)
 (20c)
(20c)
3. 结果与讨论
3.1. 温度对双手性畴壁的影响
根据表1中可以看出,铁电材料介电常数 、
、 与温度相关,且
与温度相关,且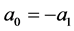 。不同的温度会使铁电材料的极化值发生改变,也会改变铁电材料的性能。研究不同温度对BTO电中性180˚双手性结构畴壁的影响,对调控铁电材料的性能具有重要作用。在本文中,我们计算了248 K、298 K、318 K三个温度下双手性结构畴壁的极化值。由于Ising畴壁是铁电材料BTO 180˚畴壁的固有形式,计算P1时,可以忽略式17(a)中的P2,得到P1的极化曲线如图4。将P1代入17(b)中进行线性化处理,得到P2的极化曲线如图5。
。不同的温度会使铁电材料的极化值发生改变,也会改变铁电材料的性能。研究不同温度对BTO电中性180˚双手性结构畴壁的影响,对调控铁电材料的性能具有重要作用。在本文中,我们计算了248 K、298 K、318 K三个温度下双手性结构畴壁的极化值。由于Ising畴壁是铁电材料BTO 180˚畴壁的固有形式,计算P1时,可以忽略式17(a)中的P2,得到P1的极化曲线如图4。将P1代入17(b)中进行线性化处理,得到P2的极化曲线如图5。
结果表明:BTO在不同的温度下有不同的极化值,其畴壁宽度也会随温度的改变而变化。铁电材料处于高于室温的环境时,其极化值增大畴壁宽度变窄;处于低于室温的环境时,其极化值会减小畴壁宽度变宽。这种现象与铁电材料介电常数相关,高于室温时 减小,
减小, 与
与 变大,吉布斯自由能也随着减小,故铁电材料的正向与负向极化值也随之减小。由于双手性畴壁的极化曲线是中心对称的,畴壁两端的极化减小使得畴壁宽度减小;低于室温时,吉布斯自由能增大,铁电材料的畴壁两端的极化值增大,导致畴壁宽度增大。
变大,吉布斯自由能也随着减小,故铁电材料的正向与负向极化值也随之减小。由于双手性畴壁的极化曲线是中心对称的,畴壁两端的极化减小使得畴壁宽度减小;低于室温时,吉布斯自由能增大,铁电材料的畴壁两端的极化值增大,导致畴壁宽度增大。
3.2. 电场对双手性畴壁的影响
铁电材料具有自发极化特性,同时其极化的大小、方向能在外电场的作用下而发生改变。施加的电场与自发极化方向相同为正电场,与极自发极化方向相反的电场为负电场。通过调控施加的电场,能得到BTO性能最优的条件。我们计算了对BTO薄膜施加正电场、负电场以及它在无电场作用下的三种情况,模拟外部电场对BTO双手性结构畴极化状态的影响。P1与P2的计算方法与3.2中相同,并假设外

Figure 4. P1 profile at different temperature
图4. 不同温度下的P1曲线
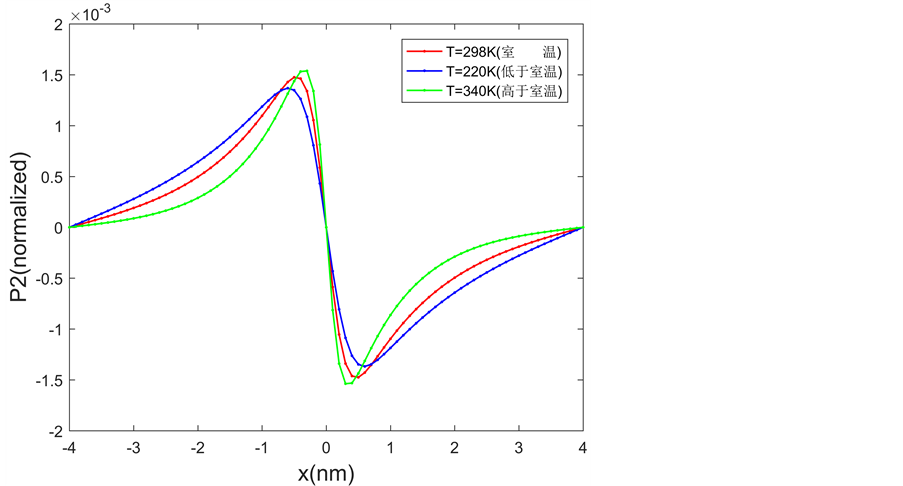
Figure 5. P2 profile at different temperature
图5. 不同温度下的P2曲线
部电场对无穷远处的极化值无影响。P1和P2在不同电场下的极化曲线如图6、图7所示。
结果表明:外部电场会改变铁电材料的极化值。对比于无电场作用的情况,正电场会使P1、P2的极化曲线向上平移,增加正向极化值;相反,负电场会使P1、P2的极化曲线向下平移,增加负向极化值。这是由于当外加电场的方向为正时,畴壁两端的极化沿正电场方向发生一定翻转,极化状态改变,导致畴壁两端极化增大,造成极化曲线上移;当外加电场方向为负时,畴壁两端的极化沿负电场方向发生一定翻转,极化状态改变,导致畴壁两端极化增大,造成极化曲线下移。

Figure 6. P1 profile at different electric field
图6. 不同电场的P1曲线
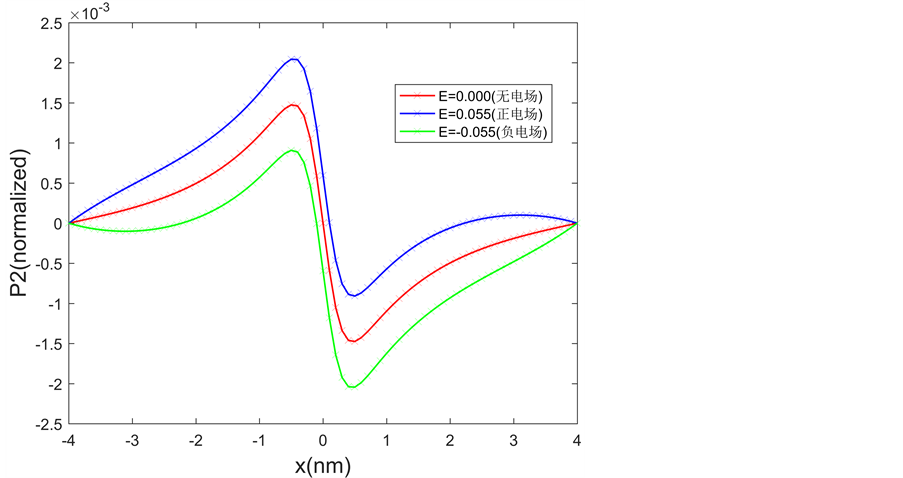
Figure 7. P2 profile at different electric field
图7. 不同电场的P2曲线
3.3. 梯度系数对双手性畴壁的影响
在描述铁电材料吉布斯自由能的梯度能量项时,引入了梯度系数张量Dijkl。同时,研究者发现BTO的无量纲梯度系数 的取值范围为0.6~2.1 [12] 。因此,不同的梯度系数会改变BTO的极化值。本文在0.6~2.1区间内选取间隔为0.5的梯度系数,研究不同梯度系数对BTO电中性180˚双手性畴壁极化状态的影响。P1与P2的计算方法与3.2中相同,通过数值计算得到P1和P2在不同梯度系数下的极化曲线如图8、图9所示:
的取值范围为0.6~2.1 [12] 。因此,不同的梯度系数会改变BTO的极化值。本文在0.6~2.1区间内选取间隔为0.5的梯度系数,研究不同梯度系数对BTO电中性180˚双手性畴壁极化状态的影响。P1与P2的计算方法与3.2中相同,通过数值计算得到P1和P2在不同梯度系数下的极化曲线如图8、图9所示:

Figure 8. P1 profile at different gradient coefficient
图8. 不同梯度系数下的P1曲线

Figure 9. P2 profile at different gradient coefficient
图9. 不同梯度系数下的P2曲线
结果表明:当BTO梯度系数 的取值范围为0.6~2.1时,随着梯度系数的增加,BTO的极化值会增加,畴壁会逐渐变宽,但畴壁中心的极化值任然为零。这是由于梯度系数的增加会使铁电材料的梯度能增加,从而使吉布斯自由能增大,导致极化值增大。双手性畴壁的极化曲线是中心对称的,畴壁两端的极化增大使得畴壁宽度增大。
的取值范围为0.6~2.1时,随着梯度系数的增加,BTO的极化值会增加,畴壁会逐渐变宽,但畴壁中心的极化值任然为零。这是由于梯度系数的增加会使铁电材料的梯度能增加,从而使吉布斯自由能增大,导致极化值增大。双手性畴壁的极化曲线是中心对称的,畴壁两端的极化增大使得畴壁宽度增大。
4. 总结
基于BTO电中性180˚双手性结构畴壁,我们模拟了温度、外部电场、梯度系数对双手性畴壁的影响。通过数值计算方法,得到了相应的极化值,并得出以下结论:
1) 温度改变BTO的极化值,并使畴壁宽度发生变化。当铁电材料处于高于室温的环境时,其极化值增大,畴壁宽度变窄;当铁电材料处于低于室温的环境时,其极化值会减小,畴壁宽度变宽;
2) 外部电场并不会改变BTO的畴壁宽度,但会改变其极化值。对比于无电场作用的情况时,正电场会使P1、P2的极化曲线向上平移,增加正向极化值;相反,负电场会使P1、P2的极化曲线向下平移,增加负向极化值;
3) 不同的梯度系数会对手性畴壁的极化值与畴壁宽度产生影响。当BTO梯度系数 的取值范围为0.6~2.1时,随着梯度系数的增加,BTO的极化值会增加,畴壁会逐渐变宽。
的取值范围为0.6~2.1时,随着梯度系数的增加,BTO的极化值会增加,畴壁会逐渐变宽。
致谢
感谢国家自然科学基金(11402222 & 11502078)和湖南省教育厅一般项目(14C1092 & 15C0535)的支持。