1. 引言
对入侵对象运行轨迹进行实时、可靠监控是入侵监测领域的重点研究内容之一，而解决这一问题的有效方法是在监测区域内设置无线传感器网络(WSN, Wireless sensor Networks)，在可预见的入侵对象运行轨迹附近区域快速部署一定数量的传感器节点，并完成对重点区域的多重监测 [1] [2] [3] 。无线传感器网络由部署在监测区域内的大量廉价微型传感器组成，它们通过无线通信方式形成多跳自组织网络系统。对原有区域内的传感器节点根据需要进行位置的调整及优化，以实现不同区域的不同覆盖要求 [4] [5] [6] 。同时要求重点区域实现多重覆盖，而一般区域实现一重覆盖。
针对以上问题，国内外学者做了很多研究。吴春琼等 [7] [8] 提出一种基于能量预测的节点调度算法，虽可节省网络能耗但降低了网络覆盖率。吴苏豫等 [9] 构建了节点连通图以发现可休眠节点，但仅适用于需大致覆盖的场景。黄守志等 [10] 提出了基于网格划分的冗余节点判定方法，但该算法仅考虑了网络完全覆盖情况，尚未考虑覆盖目标热点区域需要多重覆盖的需求。王成等 [11] [12] 提出一个基于Voronoi图的k覆盖算法，该算法可判断网络的覆盖率，且可实现多重覆盖，但该算法计算复杂度较高。实际应用中，监测区域的覆盖要求是比较复杂的，单一的覆盖要求可能导致传感器数量的过多利用及能量的无效损耗。因此，针对不同实际需求快速实现不同的覆盖重数，以降低传感器使用数量及能量损耗，具有重要的现实意义。当前研究中相关成果尚不多见。
基于此，本文提出无线传感器网络 [13] [14] [15] 下的可变k覆盖问题，并基于区域网格划分聚类 [16] 算法，设计一种移动节点的部署算法：CP-var(k)算法(var(k) algorithm based on Clustering and Prediction)。该算法可通过对节点的重新部署实现不同区域不同时间的灵活可变覆盖，在传感器节点有限的情况下，充分发挥节点作用，既可保证重点区域的多重覆盖，又可满足一般区域的覆盖要求，以消耗较少的能量为代价实现对入侵对象的有效监测。
2. 可变k覆盖问题
2.1. 问题描述
某二维平面的不同区域有不同的实时监测要求，需在不同区域部署不同数量的传感器。做如下假设：1) 按照均匀抛洒原则，区域内最多有n个可匀速移动的传感器节点；2) 传感器均为同构节点，感知半径为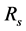
，传感半径为
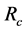，且
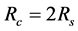，可实现网络的良好连通 [17] [18] ；3) 传感器节点的初始位置已知，传感器间可实现摩尔感知 [19] [20] ；4) 传感器节点带自备电源，可休眠及唤醒。
本入侵监测问题 [21] [22] 的系统优化目标为：发现入侵对象前，区域内所有节点保持静默状态；假设t1时刻发现入侵对象，系统将根据入侵对象的位置及运动方向快速预测其运行轨迹，确定区域覆盖策略，或者唤醒休眠传感器节点，或者命令传感器节点移动位置以快速实现不同覆盖要求。为描述方便，首先定义几个符号：1) 二维平面区域C，该区域由maxX ´ maxY确定，maxX、maxY分别为区域水平长度和
区域垂直长度。根据不同区域的覆盖要求，定义
，M为C内不同覆盖的子区域数目，
为子
区域cp的需求覆盖度，
，即该子区域所辖范围均要求满足kp重覆盖，cp同时也代表为子区域的面积，C也代表整个区域的面积；2) 监测节点vl，其中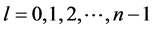
，n为最大监测节点数；3) cellij：区域内坐标为
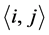的单元；4) 覆盖度：定义kcij为网格cellij的当前覆盖度，定义knij为网格cellij的需求覆盖度；5) 区域cp的覆盖满意度定义为Sat(cp)，SatT(cp)为阈值，当
时，认为本区域达到覆盖要求。
2.2. WSN中传感器节点数量的确定
假设入侵对象在一定时间范围内为规律性运行，系统可以通过监测其地理位置的实时变化情况并快速预测其运行轨迹，并通过无线传感器网络在全网内广播。将入侵对象抽象为一个点，假定其运行轨迹为一条曲线。将入侵轨迹向左、向右分别移动固定距离形成4条曲线L1~L4，L1与L2之间区域定义为重点监测区域，需实现三重覆盖；L1与L3之间以及L2与L4之间定义为次重点区域，需实现二重覆盖，其他区域为一般区域，需实现一重完全覆盖(图1)。
为提高传感器利用率并降低监测成本，需对监测区域内可用传感器数量进行限制。定义n为监测区域内所需抛洒的传感器节点数量，根据文献 [23] 可知，当3个感知半径为Rs的同质节点的感知圆盘均匀相交于一点时，各圆心连线将组成边长为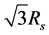
的等边三角形，此时感知圆盘的覆盖效率最高且所需节点
数量最少(图2(a))。图2中，有
，
，
，
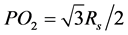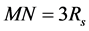。传感器节点如图2(b)实心点所示，则横向节点所需数量为
，纵向节点所需数量为
，当
时，E取值为1，否则取值为2，rem()的作用是取maxY/3Rs的余数。可计算整个区域实现一重覆盖所需节点数量为
。
设定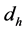
为区域纵向划分监测区域的高度，
，
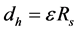为权重参数。对入侵对象来说，其在监测区域的运行轨迹越长，获取有效信息的可能性就越大。对图3(a)、图3(c)所示，入侵对象的入侵点处于左下角时入侵轨迹最长，入侵点处于左侧边界中心时入侵轨迹较长。我们忽略其他可能的低效入侵情况，拟用上述两种情况的线性组合来表示所有入侵可能。入侵对象的入侵点处于左下角时(图3(c))，重点监测区域的面积为
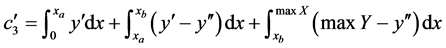
入侵对象的入侵点处于检测区域的左侧边界中心点时(图3(d))，其重点监测区域的面积为：
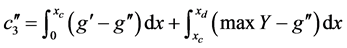
定义重点区域的抛洒面积
，其中
、
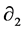为调节参数，
。
同理可得次重点监测区域和一般区域的面积c2和c1，则整个监测区域所需抛洒节点总数估计为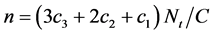
。
3. 传感器节点动态部署算法：CP-var(k)算法
3.1. 网格划分及聚类预处理
首先将监测区域划分为多个单位长度的小正方形网格，每个网格称为一个cell，如图4所示。将每个传感器节点的感知范围等效为它所覆盖的多个cell，当cell的形心被节点覆盖时，即认为该cell被整体覆盖 [17] 。
将监测区域C定义在二维平面坐标系中，假设传感器节点位置近似为其最相邻的cell的形心。为提高搜索效率，可提前将覆盖情况相同的cell聚集到一起。
3.2. CP-var(k)算法步骤
基于网格聚类算法及入侵对象的运行轨迹的预测，可通过对监测区域中节点的重新移动部署操作实现区域中不同目标区域的可变多重覆盖，这就是CP-var(k)算法的基本思想。该算法首先需对研究区域进行网格划分，根据每个网格的kcij取值进行分类，比较kcij与knij的大小得到覆盖度不足的区域及冗余节点区域，然后采取适当节点移动策略，最终以一定的满意度实现整个区域的可变k覆盖要求。具体步骤如下：
第一步：初始化。1) 在区域C中随机抛洒n个传感器节点并对其进行网格划分，计算每个网格的覆盖度kcij，得到区域初始覆盖矩阵。2) 根据入侵对象位置及方向划分不同覆盖区域及覆盖要求，快速预测出入侵轨迹曲线y = f(x)并据此确定重点监测区域、次重点监测区域与一般区域，同时向全网络广播。
第二步：网格聚类。按照8-connection近邻网格对各子区域进行网格聚类。
第三步：传感器节点与网格归类。比较网格cellij的实际覆盖度kcij与需求覆盖度knij，构造需要减少节点的集合A及需要增加节点的集合B。对于区域内所有网格，若kcij ≥ knij，则说明cellij处有冗余节点，将离此网格最远的节点加入集合A；若kcij < knij，说明此网格处覆盖节点数不足，将该网格添加到集合B。
第四步：传感器节点位置调整。根据附着在集合A的网格中的传感器节点距离集合B中网格的距离关系进行位置调整，具体为：1) 对集合B中的网格根据knij的取值进行降序排列，得到新序列Bs；2)从序列Bs首部中选择第一个网格元素，从集合A中找到与该网格元素距离最近的传感器节点，并将之移动到集合B的网格元素上；3) 根据集合A、B中各网格的当前覆盖度特征对其中元素进行增减，更新传感器节点位置及覆盖矩阵；4) 反复执行1)~3)，直到各区域的覆盖度满足阈值要求或运行时间超过最大时间要求。
4. 实验仿真与分析
4.1. 参数设置
本次仿真采用NetLogo5.2.0系统，该系统可用于模拟自然和社会现象的编程语言和建模，特别适合于模拟随时间发展的复杂系统。为方便实验，我们对模型的参数做如下取值：监测区域的大小设置为400 ´ 400；传感器节点感知半径为
；
，
，
。根据测算，监测区域内实现完全一重覆盖所需节点数为80个，实现入侵监测可变覆盖所需抛洒节点数为115个。
4.2. 仿真过程及分析
将传感器节点随机抛洒在区域C内，如图5(a)所示，其中白灰色区域表示一重覆盖区域；浅灰色区域表示二重覆盖区域，深灰色区域表示三重覆盖区域。考虑到当有入侵对象进入时，传感器节点还要进行一定规模的位置移动，随机抛洒操作完成后，既可立即进行可变k覆盖部署操作，也可先进行一定程度的覆盖盲区消减操作(如图5(b))，再进行可变k覆盖部署操作。
称具有均匀部署操作的可变k覆盖实验为方案I。传感器节点均匀部署后，入侵对象进入监测区域，假设入侵轨迹及可变k目标区域划分如图6所示。其中深灰色弧状区域为重点监测区域，宽度dh = 2Rs，需实现三重覆盖，深灰色区域中心的曲线为入侵对象的预测运行轨迹；浅灰色区域为次重点监测区域，需实现二重覆盖，其他区域需实现一重覆盖。
一旦发现入侵对象，系统将立即启动节点重新部署操作，其运行过程如图7(a)~(d)所示。可以发现图7中的传感器节点从(a)~(d)逐渐聚集，图7(d)较为清晰的展现了可变三重覆盖的特征。
称无均匀部署操作的可变k覆盖实验为方案II。该实验中，节点随机抛洒后保持静止，不进行均匀部署操作以减少能量消耗。当发现入侵对象后，系统直接进行可变k覆盖操作，如图8所示。
为验证以上两种方案的优缺点，本文分别从重点区域覆盖率和节点剩余平均能量两方面进行比较分析，如下图9和图10所示。图9中，两种方案中分别迭代50次后，方案II中重点区域覆盖率为69.11%，而方案I中为47.76%。图10中，迭代100次后，方案II中节点的剩余平均能量为72.8，方案I为46.3。出现该结果的原因是方案I中节点由于首先需要进行分散均匀分布，所以将耗费更多的时间和能量，但由于其节点分散为均匀覆盖，后期移动部署运行将会更为稳定。
为研究传感器节点数目不同情况下的性能，我们对实际节点抛洒数量进行实验考察，对比策略性能。
1) 节点数目n = 85，节点分布如图11(a)所示。由于节点数量少，监测区域中存在盲区将难以避免的，但发生入侵时，节点会根据优先级别牺牲外围一般区域的覆盖需求，首先满足重点监测区域的覆盖需求。
2) 节点数目n = 150，如图11(b)所示。在满足整个监测区域可变k覆盖的基础上产生部分冗余，即在外围一般区域也会产生部分2重甚至3重覆盖，这样会造成一定程度上节点的浪费。但如果考虑节点能量消耗或节点损坏，节点数目可适当增加。
5. 结论
本文针对二维区域入侵监测问题提出可变k覆盖问题，并基于区域网格划分聚类算法提出CP-var(k)算法对传感器节点进行重新部署优化，以实现监测区域内的可变覆盖要求。利用NetLogo进行仿真后表
(a) (b)
Figure 5. Sensor nodes randomly throwing and blind cut. (a) Randomly throwing; (b) Blind cut
图5. 传感器节点随机抛洒及覆盖盲区消减。(a) 初始随机抛洒；(b) 覆盖盲区消减
Figure 6. Intrusion trajectory and variable k coverage region partition
图6. 入侵轨迹及可变k覆盖区域划分
(a) (b) (c) (d)
Figure 7. Sensor node deployment process (uniform deployment operation)
图7. 传感器节点移动部署过程(有均匀部署操作)
(a) (b)
Figure 8. Sensor node deployment process (no uniform deployment operation)
图8. 传感器节点移动部署过程(无均匀部署操作)
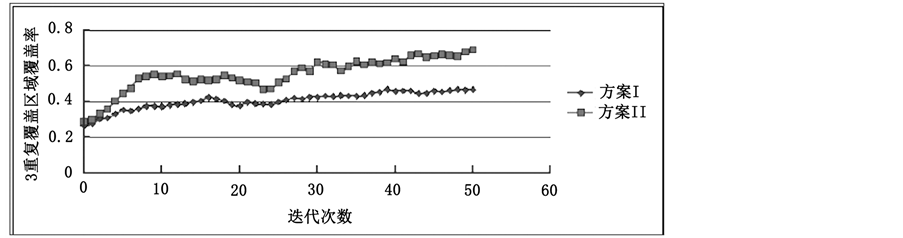
Figure 9. Change curve of coverage in key monitoring area
图9. 重点监测区域中覆盖率变化曲线
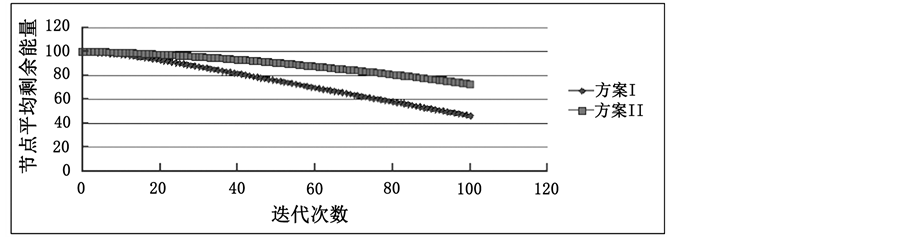
Figure 10. Average energy curve of node residual energy (initial energy is 100)
图10. 节点剩余平均能量曲线(节点初始能量为100)
(a)(b)
Figure 11. Variation of sensor nodes. (a) A large number of nodes; (b) Less number of nodes
图11. 传感器节点变化情况。(a) 节点数量较多；(b) 节点数量较少
明，在节点数目有限的前提下，该算法能以较快的时间和较少的能量消耗对节点进行良好部署，从而验证了算法的有效性。但本文只是以单点入侵监测为例进行了分析，后期可以此为基础研究多点入侵以及三维区域的可变覆盖问题。
基金项目
本文受国家大学生创新创业项目资助(No. 201512331020)。