1. 引言
钙钛矿型的铁电氧化物,如PbTiO3和Pb(Zr, Ti)O3固溶体,均属于电子陶瓷材料,其具有铁电性及大的压电响应和高介电常数等相关机电性能 [1] 。由于其优越的性能,铁电钙钛矿氧化物在器件方面的应用已引起广泛地关注,如高密度非易失性随机存取存储器、传感器、机电设备等 [2] [3] 。
第一性原理计算方法在预测材料性质方面起着非常重要的作用。虽然传统的基于局域密度近似 [4] 和广义梯度近似 [5] 的计算方法可以较好地预测材料基态的物理性质,但计算得到的带隙与实验值并不符合。最近人们已经应用杂化泛函理论来研究一些氧化物 [6] 的物理性质,包括VO2、V2O3、Ti2O3、LaTiO3和YTiO3等,而且得到与实验比较吻合的结果 [7] [8] [9] [10] 。然而,对于铁电材料而言,基于杂化泛函的第一性原理研究还比较少。本文以铁电材料PbTiO3为例,利用杂化泛函理论研究其块体材料的晶体结构和电子结构。我们发现基于PBE交换关联势,当长程Hartree-Fork关联项为0.325时杂化泛函所得的带隙值与实验结果相吻合。基于PBE交换关联势所得的晶体结构与实验值相差较大,而基于PW交换关联势的计算表明,当长程Hartree-Fork关联项等于0.2时,杂化泛函所得的晶体结构与实验结果比较吻合,但此时带隙值小于实验值。
2. 计算方法
我们使用基于投影缀加平面波方法(PAW)的第一性原理软件包VASP [11] [12] 。采用基于PBE [13] 和PW [14] 交换关联势以及考虑长程Hartree-Fork项作用的杂化泛函方法 [15] 来研究PbTiO3的晶体结构和电子结构。我们考虑Pb6s26p24个价电子,Ti4d35s14个价电子,O 2s2p46个价电子的贡献。平面波截断能量为600 eV。k点网格为6 × 6 × 6。收敛标准为10−5 eV。在杂化泛函理论中,我们用Hartree-Fock交换项来替换部分短程的PBE(PW)交换势, 具体表达式如下:
 (1)
(1)
其中α是Hartree-Fock项所占比例。在计算过程中,我们考察不同α值对PbTiO3电子结构和晶体结构的影响,寻找与实验相符合的α值。
3. 计算结果与讨论
图1为PbTiO3的晶体结构图。左图为铁电相,右图为顺电相。其中黑色为Pb元素,蓝色为Ti元素,红色为O元素。表1为PbTiO3晶体结构的实验值 [16] 。
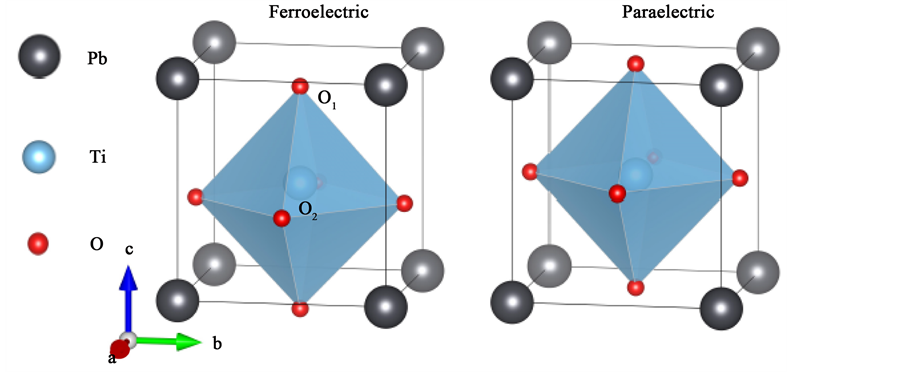
Figure 1. The crystal structure of PbTiO3: the left is ferroelectric phase, the right is paraelectric phase (Pb, Ti, O are located in corner, body center, face center, respectively)
图1. PbTiO3的晶体结构图:左图为铁电相,右图为顺电相(Pb, Ti, O分别位于顶点,体心和面心)

Table 1. The experimental value of PbTiO3 crystal structure
表1. PbTiO3晶体结构实验值
我们在实验的晶体结构 [16] 下利用基于PBE交换关联势的杂化泛函理论,研究长程Hartree-Fork库伦关联项(α)对铁电材料PbTiO3带隙的影响,如图2所示,其中红色虚线为实验值 [17] 。从图中我们发现,计算所得的带隙值随α值的增大而增大,当α为0.325时带隙值与实验值较为接近。图3是此时计算得到的PbTiO3总态密度和分波态密度。我们发现基于PBE交换关联势的杂化泛函理论在带隙计算上的优势非常明显,选用合适的α值,可得到与实验值十分吻合的计算结果。
基于PBE交换关联势的杂化泛函理论我们进一步研究α的选取对晶体结构计算的影响。如表2所示,随着α值的增大,晶格常数a逐渐减小,与实验值差距逐渐拉大,而c逐渐减小,与实验值越来越接近,但仍大于实验值,因此计算得到的c/a的值始终大于实验值。显然利用PBE交换关联势的杂化泛函计算得到的晶体结构与实验值相差较大,因此我们利用PW交换关联势的杂化泛函对PbTiO3的晶体结构进行计算。如表3所示,随着α值的逐渐增大,计算得到的晶格常数a值逐渐减小而c值逐渐增大,c/a的值也因此逐渐增大,当α增加至0.2时,计算得到的c/a的值与实验值比较吻合,其晶体结构数据见表4。另一方面,能带结构计算结果显示,随着α值的逐渐增大,带隙值也逐渐增大。当α = 0.2时,带隙值约为2.46 eV,这远小于实验值。而选取α值0.35时,计算所得的带隙值与实验值较为吻合(3.35 eV),但其晶格常数与实验值相差较大。综上所述,晶体结构和电子结构的计算结果表明杂化泛函对于铁电材料PbTiO3性质的计算的适用性还有待商榷 [18] 。
4. 总结
基于杂化泛函理论,我们考察了长程Hartree-Fork项在交换关联势中所占比例(α)对铁电材料PbTiO3晶体结构和电子结构的影响。我们发现基于PBE交换关联势,当α等于0.325时杂化泛函所得的带隙值与实验结果相吻合。另外,基于PBE和PW交换关联势我们分别研究了α对晶体结构的影响,基于PBE交换关联势的结果与实验值相差较大。而基于PW交换关联势的计算表明,当α等于0.2时的杂化泛函
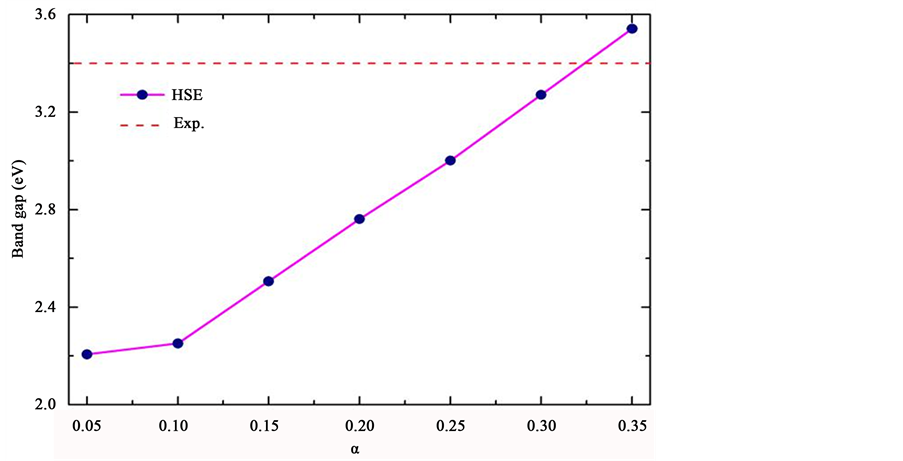
Figure 2. Band gap of PbTiO3 as a function of α. The red dash line is the experimental value
图2. 计算得到的PbTiO3带隙值与Hartree-Fork项(α)的依赖关系,其中红色虚线为实验值 [17]
表2. 基于PBE交换关联势杂化泛函方法计算所得PbTiO3的晶格常数a,c,c/a以及带隙Egap。表中最右列是实验测量结果
表3. 基于PW交换关联势杂化泛函方法计算所得PbTiO3的晶格常数a,c,c/a以及带隙Egap。表中最右列是实验测量结果
表4. 基于PW交换关联势(α = 0.2) PbTiO3的晶体结构值以及与实验结果的比较
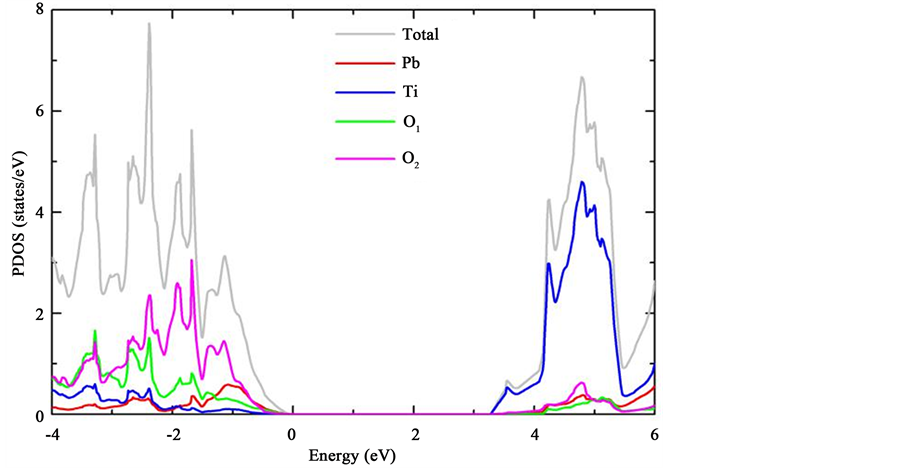
Figure 3. The density of states (DOS) of PbTiO3: The grey line is the total DOS. Red is for Pb. Blue is for Ti. Green and pink is for O1 and O2, respectively
图3. PbTiO3的电子结构态密度:灰色为PbTiO3的总态密度,红色为Pb离子的态密度,蓝色为Ti离子的态密度,绿色和玫红色分别代表O1和O2的态密度
所得的晶体结构与实验结果比较吻合,但此时带隙值却小于实验值。这些结果表明杂化泛函对于铁电材料PbTiO3的适用性还有待商榷 [18] 。