1. 引言
由线路和变压器等构成的电力网是连接发电机和负荷用户的桥梁,其安全性和可靠性是直接影响电源连续供电和用户连续用电的关键因素。
为确保电力网安全可靠运行,布置在电力网各处的测量仪表需要对注入节点的有功功率和无功功率大小、线路传输的有功功率和无功功率大小等重要数据进行连续不断检测。它们通过SCADA系统传送至电网控制中心,再通过状态估计系统剔除不良数据才能得到可信的电力网运行状态数据(如节点电压幅值和相位) [1] [2] [3] 。基于这些可信的运行状态数据,控制中心才能实施最优潮流分析、经济调度决策、安全校正控制等 [4] ,确保整个电力系统安全可靠运行。
黑客通过篡改检测数据攻击电网的目的,轻则使电网控制中心得到虚假数据而从中获利(如篡改关口表有功功率大小),重则使电网控制中心收到虚假的阻塞信息、使安全校正系统自动响应、导致系统陷入真实的阻塞状况或更严重的停电事故 [5] 。如2015年12月23日乌克兰发生大规模的停电事故,被认为是第一起网络攻击直接导致停电事故的案例 [6] 。由于电网控制中心的状态估计系统对不良数据有过滤作用,一般随机性不良数据都无法躲过该系统的过滤作用 [7] [8] 。因此,黑客通过篡改检测数据发起的攻击能否成功,关键是这些虚假数据能否躲过状态估计系统的过滤。
Liu Y.等人在2009年提出了电力系统状态估计欺诈性数据的概念 [9] ,即攻击者可以通过检测方法的漏洞,蓄意改变状态估计结果,使电力系统无法安全可靠的运行。2011年Yuan Y.等人提出了负荷再分配的攻击模型 [10] ,随后Qin Z.等人在2012年提出了无法被辨识的攻击的概念 [11] ,并构建了该方法的攻击模型。为躲过状态估计系统对虚假不良数据的过滤作用,通常攻击向量的建模要在全电网结构和参数已知的条件下进行,这增大了攻击向量建模的难度 [5] 。实际上,基于全电网结构和参数的建模方法,使模型呈现为含0或1范数的大规模复杂问题、难以求解 [12] 。因此,研究信息量需求小且易于求解的攻击向量建模方法,是降低发起虚假数据攻击代价的关键。
本文提出了一种电力系统最小虚假数据攻击向量的建模方法。这种方法以被攻击电网的局部子网为对象建模,需要的信息量很小。本文模型中通过引入虚假数据攻击导致线路输电阻塞的约束,使电网控制中心的安全校正系统产生响应,达到严重影响电网安全可靠运行的目的。这种攻击向量模型以满足节点功率平衡方程约束为条件,巧妙躲过电网控制中心状态估计系统的过滤作用,因此是一种小代价、高效能的攻击向量模型。
2. 攻击向量和虚假数据
针对直流潮流的情况,用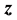 表示SCADA系统采集的电力系统量测量(包括节点注入有功功率和线路有功功率、是
表示SCADA系统采集的电力系统量测量(包括节点注入有功功率和线路有功功率、是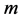 维列向量),用
维列向量),用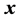 和
和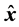 分别表示系统的状态量及其状态估计值(节点电压幅值和相位、是
分别表示系统的状态量及其状态估计值(节点电压幅值和相位、是 维列向量),用
维列向量),用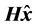 表示直流潮流下量测量的估计值(
表示直流潮流下量测量的估计值(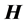 是直流潮流下量测量方程组的雅可比矩阵),用
是直流潮流下量测量方程组的雅可比矩阵),用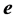 表示测量误差向量。则有量测量方程:
表示测量误差向量。则有量测量方程:
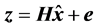 (1)
(1)
定义残差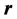 为
为
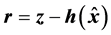 (2)
(2)
式(2)中 表示直流潮流下量测量方程组,电力系统状态估计就是找出使
表示直流潮流下量测量方程组,电力系统状态估计就是找出使 最小的
最小的 的估计值
的估计值 。这运用最小二乘解即可求得。
。这运用最小二乘解即可求得。
正常情况下,残差 由测量噪声引起且非常小,它远远小于统计学卡方分布的允许误差门坎值
由测量噪声引起且非常小,它远远小于统计学卡方分布的允许误差门坎值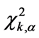 (其中
(其中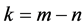 是自由度、
是自由度、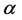 是显著性水平如0.05),这是量测量未受不良数据侵扰的标志。若构造一个与
是显著性水平如0.05),这是量测量未受不良数据侵扰的标志。若构造一个与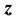 同维的向量
同维的向量 、让量测量由
、让量测量由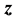 变成
变成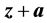 、且仍然使残差
、且仍然使残差 小于统计学卡方分布的允许误差门坎值
小于统计学卡方分布的允许误差门坎值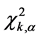 (即躲过状态估计系统的过滤作用),则是一个成功的虚假数据攻击。称
(即躲过状态估计系统的过滤作用),则是一个成功的虚假数据攻击。称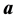 为攻击向量、
为攻击向量、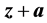 为虚假量测量或虚假数据。因此,发起一个虚假数据攻击的关键,在于构建一个能够躲过状态估计系统过滤作用的攻击向量
为虚假量测量或虚假数据。因此,发起一个虚假数据攻击的关键,在于构建一个能够躲过状态估计系统过滤作用的攻击向量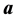 。上述分析虽基于直流潮流(为简明),但也适用交流潮流的情况。若添加攻击向量
。上述分析虽基于直流潮流(为简明),但也适用交流潮流的情况。若添加攻击向量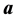 的虚假数据
的虚假数据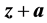 对应的最小二乘解残差
对应的最小二乘解残差 与不添加
与不添加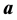 时的最小二乘解残差
时的最小二乘解残差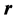 相等,则称虚假数据
相等,则称虚假数据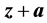 为完美欺诈性数据 [3] 。
为完美欺诈性数据 [3] 。
3. 最小虚假数据攻击向量的建模
生成一个攻击向量必须基于电网的拓扑结构和参数。对黑客而言,掌握电网某个局部的拓扑结构和参数比掌握其全部信息要容易得多、简单得多。为此,下面以受攻击电网的一个局部子环网为对象来分析。
将受攻击的电力网划分成局部子环网(有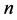 个节点)和外网两个部分,如图1所示。外网中两者的边界节点编号为
个节点)和外网两个部分,如图1所示。外网中两者的边界节点编号为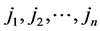 。局部子环网中节点的编号为
。局部子环网中节点的编号为 ,其中局部子环网的节点数大于边界节点数(
,其中局部子环网的节点数大于边界节点数( )。若改变局部子环网中各节点注入功率的分布、如叠加一个攻击向量
)。若改变局部子环网中各节点注入功率的分布、如叠加一个攻击向量 ,同时确保这些边界节点的电压和局部子环网注入外网的功率不变(由局部子环网的环形结构保障)、确保局部子网的节点注入功率满足电路规律,则
,同时确保这些边界节点的电压和局部子环网注入外网的功率不变(由局部子环网的环形结构保障)、确保局部子网的节点注入功率满足电路规律,则 就是一个有效的虚假数据攻击。
就是一个有效的虚假数据攻击。

Figure 1. Local sub-network and external network
图1. 局部子环网和外网
按上述思路,可构建出如下的攻击向量模型:
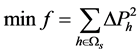 (3)
(3)
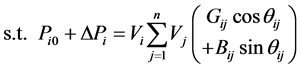 (4)
(4)
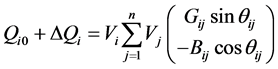 (5)
(5)
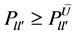 (6)
(6)
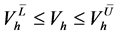 (7)
(7)
 (8)
(8)
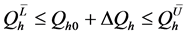 (9)
(9)
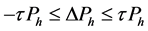 (10)
(10)
 (11)
(11)
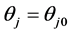 (12)
(12)
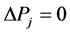 (13)
(13)
 (14)
(14)
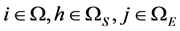
其中: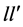 是虚假数据攻击欲达到的输电阻塞线路、
是虚假数据攻击欲达到的输电阻塞线路、 和
和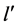 是它的两个节点编号,通常取局部子环网中容易发生阻塞的一条线路。
是它的两个节点编号,通常取局部子环网中容易发生阻塞的一条线路。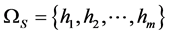 是局部子环网的节点编号集合,
是局部子环网的节点编号集合,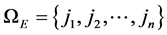 是外网中边界节点编号的集合,
是外网中边界节点编号的集合,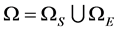 。上标
。上标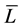 和
和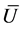 分别表示变量的下界和上界。
分别表示变量的下界和上界。 和
和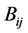 分别是局部子环网与外网边界节点构成的电网的节点导纳矩阵中元素的实部和虚部。下标0表示实际测量值。
分别是局部子环网与外网边界节点构成的电网的节点导纳矩阵中元素的实部和虚部。下标0表示实际测量值。
式(3)是目标函数,即最小化局部子环网节点注入功率增量的平方和、使攻击向量的模长尽可能小。式(4)和(5)是节点功率平衡约束。式(6)是线路阻塞约束,引入它、使虚假数据攻击达到使安全校正系统自动响应、导致系统陷入真实的阻塞状况或更严重的停电事故。式(7)~(10)是局部子环网变量的上限和下限约束,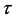 是给定的局部子环网节点注入功率增量的允许百分数(如10%,参照当前真实负荷和各节点可能出现的最大负荷确定)。式(11)~(14)是外网中边界节点变量的约束,是使外网边界节点的电压和注入功率保持不变、从而使外网节点功率平衡方程仍然成立。
是给定的局部子环网节点注入功率增量的允许百分数(如10%,参照当前真实负荷和各节点可能出现的最大负荷确定)。式(11)~(14)是外网中边界节点变量的约束,是使外网边界节点的电压和注入功率保持不变、从而使外网节点功率平衡方程仍然成立。
求解上述模型,得到的局部子环网内电表测量值增量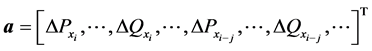 就是攻击向量,其中
就是攻击向量,其中 、
、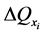 是局部子环网内节点注入功率的增量,
是局部子环网内节点注入功率的增量,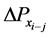 、
、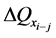 是局部子环网内线路潮流的增量。将它在SCADA系统中叠加到测量数据
是局部子环网内线路潮流的增量。将它在SCADA系统中叠加到测量数据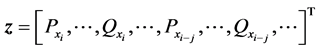 上、并送到电网控
上、并送到电网控
制中心,就成功地发射了一次虚假数据攻击。因为,该攻击向量的构造确保将它叠加到原有检测值上后仍然使电网各节点满足功率平衡约束、成功躲过状态估计软件的过滤作用。
4. 仿真与分析
为了验证上述模型的可行性,采用IEEE 14节点系统和IEEE 30节点系统构建攻击向量并进行仿真与分析,通过鲁棒状态估计方法对该攻击模型作状态估计和残差检验 [13] 。
① 对图2所示IEEE 14节点系统,其结构和运行参数取自文献 [14] 。取图3所示节点1至5的局部子环网建立数学模型,并将由文献 [15] 给定参数决定的其运行状态参数作为SCADA系统的测量数据。表1和表2给出了仿真计算结果。

Table 1. Attack vector at different line congestion
表1. 设置不同线路阻塞时的攻击向量

Table 2. Comparison of residual before and after attack
表2. 攻击前后残差的对比
表1给出了设置不同线路阻塞时的攻击向量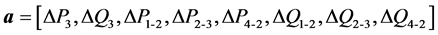 。可见,设置线路1-2出现阻塞(加剧攻击效果)建模时,得到的攻击向量模长为0.5493、最小,由此发起虚假数据攻击将更不易被运行调度人员发觉(因为改变真实测量值的幅度最小)。因此称之为最小虚假数据攻击。此外,本例中攻击者在14个节点中只选取5个节点的子环网进行攻击。更具体地,对于一共有32个量测电表的电网,只需篡改8个电表的数据便可实现攻击。因此,这是一种攻击代价小(数据容易获取且攻击向量易于构建)、易于实现的虚假数据攻击。
。可见,设置线路1-2出现阻塞(加剧攻击效果)建模时,得到的攻击向量模长为0.5493、最小,由此发起虚假数据攻击将更不易被运行调度人员发觉(因为改变真实测量值的幅度最小)。因此称之为最小虚假数据攻击。此外,本例中攻击者在14个节点中只选取5个节点的子环网进行攻击。更具体地,对于一共有32个量测电表的电网,只需篡改8个电表的数据便可实现攻击。因此,这是一种攻击代价小(数据容易获取且攻击向量易于构建)、易于实现的虚假数据攻击。
表2给出了表1的攻击向量作用下的残差。按统计学理论,此时的自由度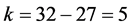 、选择显著性水平为0.05,查表得到卡方分布的检测门槛值
、选择显著性水平为0.05,查表得到卡方分布的检测门槛值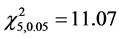 。表2中攻击前的残差为0.26316、攻击后的最大残差为0.27682,都远小于门槛值
。表2中攻击前的残差为0.26316、攻击后的最大残差为0.27682,都远小于门槛值 。这表明,按本方模型构建的攻击向量的确能躲过状态估计系统的过滤作用、从而产生有效攻击。同时攻击后的残差与攻击前的残差近似相等,表明发起该攻击的虚假数据属于完美欺诈性数据。
。这表明,按本方模型构建的攻击向量的确能躲过状态估计系统的过滤作用、从而产生有效攻击。同时攻击后的残差与攻击前的残差近似相等,表明发起该攻击的虚假数据属于完美欺诈性数据。
② 对图4所示IEEE 30 节点系统,其结构和运行参数取自文献 [14] 。取图5所示节点1至7的局部子环网建立数学模型,并将由文献 [15] 给定参数决定的其运行状态参数作为SCADA系统的测量数据。表3和表4给出了仿真计算结果。

Table 3. Attack vector at different line congestion
表3. 设置不同线路阻塞时的攻击向量

Table 4. Comparison of residual before and after attack
表4. 攻击前后残差的对比
表3给出了设置不同线路阻塞时的攻击向量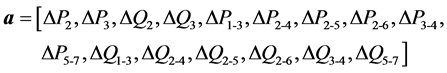 。可
。可
见,设置线路5-7出现阻塞(加剧攻击效果)建模时,得到的攻击向量模长为0.2126、最小,由此发起虚假数据攻击将更不易被运行调度人员发觉(因为改变真实测量值的幅度最小)。因此称之为最小虚假数据攻击。而设置线路2-4、2-5、2-6阻塞时,模长非常大,因此需要篡改的电表量测值幅度很大,不宜作为攻击向量。此外,本例中攻击者在30个节点中只选取7个节点的子环网进行攻击。更具体地,对于一共有78个量测电表的电网,只需篡改16个电表的数据便可实现攻击。因此,这是一种攻击代价小(数据容易获取且攻击向量易于构建)、易于实现的虚假数据攻击。
表4给出了表3的攻击向量作用下的残差。按统计学理论,此时的自由度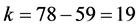 、选择显著性水平为0.05,查表得到卡方分布的检测门槛值
、选择显著性水平为0.05,查表得到卡方分布的检测门槛值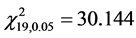 。表2中攻击前的残差为
。表2中攻击前的残差为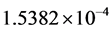 、攻击后的最大残差为
、攻击后的最大残差为 ,都远小于门槛值
,都远小于门槛值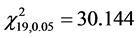 。这表明,按本方模型构建的攻击向量的确能躲过状态估计系统的过滤作用、从而产生有效攻击。同时攻击后的最大残差比攻击前小了27%,表明发起该攻击的虚假数据属于完美欺诈性数据。
。这表明,按本方模型构建的攻击向量的确能躲过状态估计系统的过滤作用、从而产生有效攻击。同时攻击后的最大残差比攻击前小了27%,表明发起该攻击的虚假数据属于完美欺诈性数据。
5. 结论
本文构建攻击向量的方法从受攻击电网的局部子环网出发建模,需要掌握的电网信息量少、易于实现。在本文方法得到的攻击向量作用下,状态估计的残差值远小于卡方分布的允许误差,并且与攻击前的残差值变化不大,因此能有效躲过电力系统状态估计软件的过滤作用,形成有效的虚假数据攻击。模型中通过引入虚假数据攻击导致线路输电阻塞的约束,使电网控制中心的安全校正系统产生响应,达到严重影响电网安全可靠运行的目的。此外,本文方法得到的攻击向量模长小,因此是一种最小虚假数据攻击。这种攻击能躲过传统电力系统状态估计的过滤作用,应对该类攻击的检测手段和方法有待深入研究。
基金项目
国家自然科学基金资助(编号51477104);深圳市科技研发资金资助(编号GJHZ20150313093836007);深圳市战略新兴产业发展专项资金资助(编号JCYJ20150525092941041)。