1. 引言
作为电网中的主要电气设备,电力变压器对电能的经济传输、灵活分配、安全使用等具有重要意义 [1] [2] 。随着城市用电负荷的不断增加,干式变压器以其无油、防火、寿命长、节能低噪、维护简单、安全可靠等诸多优点得到越来越广泛的应用 [3] ,尤其是在配电变压器中,干式变压器所占的比例愈来愈大。干式变压器内部温度的高低和分布对变压器的工作状况有直接的影响,在实际运行中,热问题是影响变压器运行状态的关键因素 [4] ,温升过高对变压器的传输效率和使用寿命都有较大影响 [5] [6] ,干式变压器的绝缘性能与其内部的产热和散热情况密切相关,内部产热与散热不均衡会影响绕组绝缘的热寿命 [7] [8] 。树脂绝缘干式变压器的绝缘介质是环氧树脂,其具有较高绝缘系统温度等级,此种类型的变压器具有油浸式变压器无可比拟的优点,其是不足之处在于导热性能相对较差。变压器温度场的设计及散热结构的合理性与其安全可靠性密切相关。因此,得到变压器的热分布特性,避免变压器出现温度过高的情况,对保障变压器的可靠运行和电网供电安全显得尤其重要。
长期以来,变压器内部的热特性都是通过经验公式来获得,其中IEEE Std C57.91-2011和IEC 354标准中推荐的热点温度计算模型,是最基本的且实际应用最为广泛的模型 [9] [10] 。而经验公式又是由大量的实验得到,通过这种方法得到变压器内部的最高温度,但难以得出整个变压器内部的温度场分布情况。本文基于传热学基础理论,利用有限元法对变压器内部的温度场进行了仿真,建立了变压器的二维和三维物理模型,研究了周围环境温度和负载率变化对变压器温度场的影响,得到了变压器内部温度场的大致分布规律,对变压器的设计和状态监测具有一定的指导意义。基于变压器内部的温度分布可以指导热电偶的掩埋地点,从而极大地节约成本,避免盲目掩埋造成的浪费。通过研究负载率对变压器内部温度分布的影响,可以对变压器的运行进行管理,以达到最佳的经济效率。
2. 物理模型及参数设置
2.1. 热源的计算
以SC8-1000/10干式变压器为研究对象。容量为1000 kVA的配电变压器,其变比10 kV/0.4kV。长宽高分别为1475 mm × 1350 mm × 225 mm。低压绕组与铁心之间气道为15 mm,高压绕组与低压绕组之间气道为34 mm。变压器的热源即为变压器铁心、低压绕组、高压绕组产生的损耗,在仿真中用单位体积热源表示,将损耗除以体积即得到单位体积热源。铁心损耗及空载损耗为固定损耗。空载时电流很小,可以忽略不计。假设变压器在空载运行时的损耗即为磁通在铁芯中的损耗,因此把空载损耗定义成为铁损。所选变压器的空载损耗P0为2430 W。图1为10 kV干式变压器的三维模型,其中铁芯尺寸的长宽高分别为1334 mm、178 mm和1156 mm,铁心柱直径为178 mm,上下铁轭高度为178 mm。铁心柱截面为圆形,铁轭截面为矩形。铁芯体积为3个铁心柱体积与上下两个铁轭的体积之和,其大小为0.149 m3,铁心单位体积热源为16.31 kW/m3。
变压器绕组损耗即为变压器的负载损耗,与负载电流大小的平方成正比。经过大量实验数据及经验公式得到不同负载大小时负载损耗的计算式,在GB/TB13462-92中也给出了相应系数的取值,负载损耗P1 = Ktβ2PK。Kt为负载波动损耗系数,β为负荷率,PK为短路损耗。应用Kt对变压器损耗进行动态计算,可极大地提高计算精度。选定的变压器计算得到绕组体积为0.105 m3。
2.2. 各部分材料参数
铁芯是由Z10冷轧硅钢片叠装而成,直径大小225 mm,其温度场分布关于r = 0处对称。其余边界为对流换热边界,发热由磁滞涡流损耗引起。变压器的空载损耗P0为2430 W,硅钢片导热系数kg = 18 W/(m∙K),密度为7650 kg/m3,常压热容Cp = 477.3 J/(kg∙K)。低压绕组的绕线方式为箔式,铜箔间绝缘层为绝缘纸,将绝缘纸设为绕组表面进行辐射设置。各边界为自然冷却边界,铜导热系数kt = 398 W/(m∙K),绝缘纸导热系数kj = (0.2~0.3) W/(m∙K),其表面辐射系数为0.26,空气导热系数k = 0.026 W/(m∙K)。绕组铜的密度为8700 kg/m3,热容量477.3 J/(kg∙K)。高压绕组为层式,共9层,每层由3 mm的铜箔绕制而成,采用预浸聚脂非织布进行层间绝缘,绕制完毕后于真空罐中用环氧树脂进行浇注,其外部有包封绝缘。考虑最后用环氧树脂进行浇注,将其外部辐射表面设为环氧树脂进行仿真。各边界为换热边界,树脂的导热系数为0.002 6 W/(m∙K)。铁芯和线圈的各换热边界条件的差异通过不同的对流和辐射系数来体现。在自然冷却条件下,室温设置为30℃,换热系数α = 10~14 W/(m2∙K),树脂表面黑度为0.9。
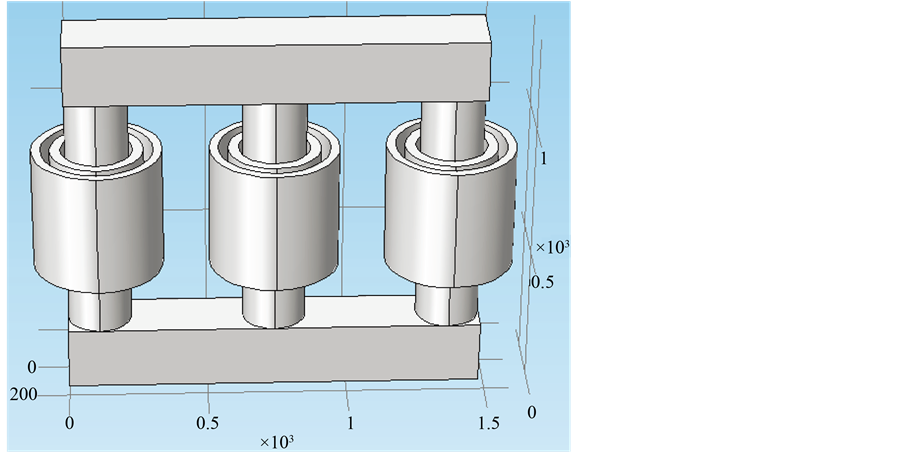
Figure 1. Three-dimensional model of the 10 kV transformer
图1. 10 kV变压器三维模型
2.3. 控制方程
空气的流动和散热要遵循质量守恒定律、动量守恒定律及能量守恒定律。其控制方程可由以下方程式组表达 [11] :
 (1)
(1)
式(1)中:ρ为流体密度;u、v和w为流体速度矢量在x、y和z方向的分量;p为流场的压力;μ为流体运动粘性系数;Fu、Fv和Fw为动量守恒方程的广义源项;T为流体温度;k为流体的导热系数;c为流体比热容;▽2为调和算子。辐射换热和另外两种热量传递方式区别在于:在发射时是热能转化为辐射能,而在吸收时又以辐射能转换为热能。辐射换热量可描述为:
 (2)
(2)
式(2)中,Q为辐射面单位时间内发出的热辐射量;ε为表面发射率;σ为斯蒂芬-玻尔兹曼常数;T0为辐射面表面温度;T为周围空气温度。
3. 计算结果及分析
为得到变压器内部在不同建模下的内部温度场,建立不同物理模型对变压器温度场进行仿真。对铁芯单位体积热源、绕组单位体积热源、外部空气温度、大气压,设置外部环境温度为30℃。该变压器的全局参数定义如表1所示。进行材料的定义、热源、边界条件、散热方式以及各参数的设置等,散热考虑导体传热、自然冷却、辐射。
研究温度场随着环境温度的变化情况时,采用负载率为80%进行研究,此时Kt = 1.042,PK = 9300 W,通过对选定的变压器绕组进行计算,得到绕组单位体积热源为59.07 kW/m3。图2为建立二维模型利用有限元法计算得到的温度场分布情况。其中(a)为由三维温度场视图,(b)为二维温度场及等温视图。
通过图2可以直观地看出变压器内部的温度场的分布,还能得到某个准确坐标处的温度大小。由图2可判断该变压器在外界环境温度为303 K、选择固体传热物理模块、负载率为80%时,其正常工作时的最高温度为373.06 K。由于低压绕组处于高压绕组和铁芯中间,散热条件最差,所以变压器工作的最高温升点在变压器低压绕组,据此可以看出变压器是否会超出正常运行温度。在变压器内部,由于变压器轴向尺寸相对于纵向尺寸较小,温度梯度变化不大。由于绕组在径向厚度相对于轴向很小,在同一轴向坐标位置上,其温度几乎是相同的,对于铁芯,可以看到如图示的等温线图,由于散热条件的影响,使得靠近低压绕组处的温度趋近于铁芯内侧处的温度,形成一条等温线。在三维物理模型的建立中,采用的所有参数与建立二维模型时相同。图3为建立三维模型利用有限元法计算得到的温度场分布。
由图3可以看出,建立三维的固体传热物理模型与建立二维物理模型时得到的温度场的温度虽然有一定的改变,但误差在3 K范围以内。通过两种物理模型的对比可以看出模型建立的准确度。通过改变
表1. 全局参数
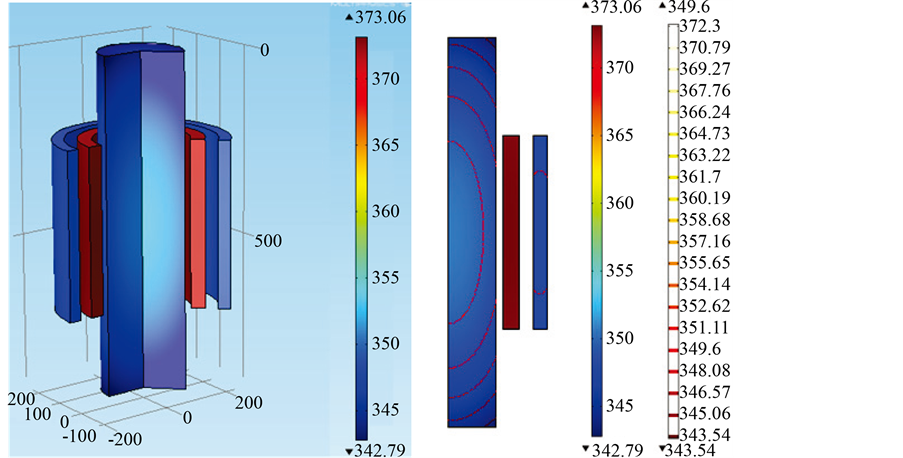
Figure 2. Temperature field in the 2D model (80% load)
图2. 二维模型对应的温度场(80%负载)

Figure 3. Temperature field in the 3D model (80% load)
图3. 三维模型对应的温度场(80%负载)
三维变压器模型的外部环境温度,得到了变压器内部出现的最高温度随着外部环境温度的变化情况如表2和图4所示。
由图4可以看出随着环境温度的提高,变压器内部的最高温度和最低温度都呈近似线性增加的趋势。可根据研究变压器随着外部环境温度的变化情况预测在发生高温和超低温时变压器内部的最高温度和最低温度情况,以此来判断变压器的运行情况。改变变压器的负载率,得到不同条件下变压器的内部温度场,在此建立了变压器的二维固体传热物理模型,考虑变压器内部的固体传热、热辐射、自然冷却,外部环境温度都设置为303 K。图5为变压器负载率40%时的温度场分布图。从图5可以看出,负载率为40 %时,变压器的最高温度为351.59 K,此时变压器最高温度点出现在铁芯,与前面负载率为80%时不同。这是由于随着变压器负载率的提高,绕组损耗越来越大。根据研究发现,负载率超过56%时,变压器的最高温度点由铁芯变为变压器的低压绕组。
图6为变压器的最高温度值与最低温度值随着变压器负载率的变化情况,随着变压器的负载率增加,变压器内部的温度场的分布也发生了变化。随着负载率的增加,变压器的负载损耗增加,单位体积热源增加,导致变压器内部的温升增加。通过对不同负载率情况下变压器内部温度场分布情况的研究,了解不同情况下温度分布,可以针对在不同的使用情况下变压器的负荷率一般是在什么范围内来针对性地设置热电偶掩埋地点以及对温升的大致情况有所了解,有效地对变压器的运行状态进行监测。
表2. 全局参数
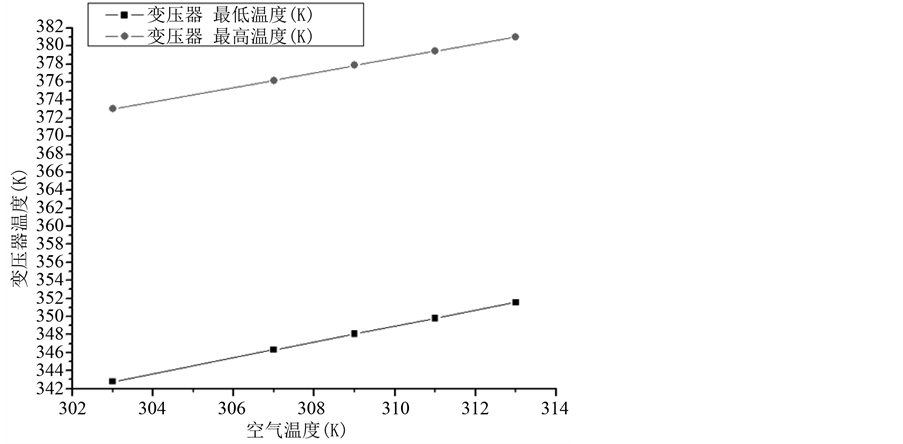
Figure 4. Transformer temperature curve with outside temperature changes
图4. 变压器温度随外界温度变化曲线
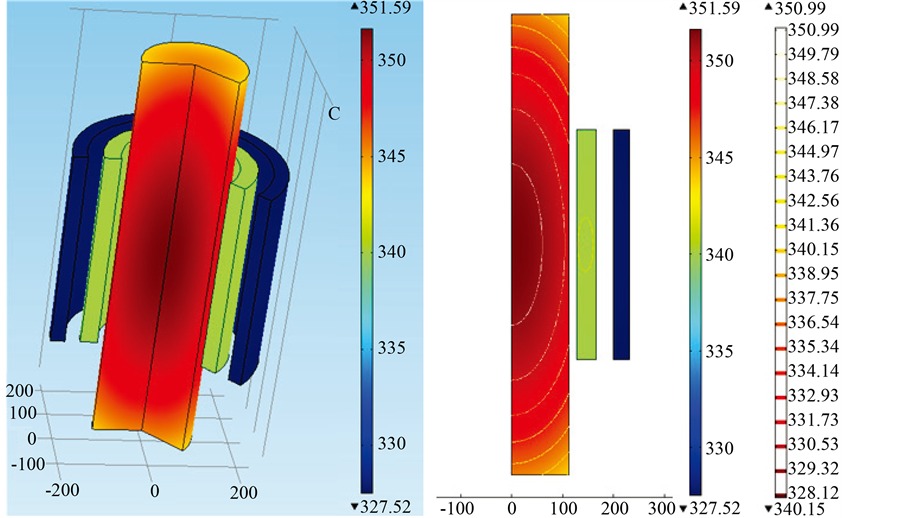
Figure 5. Temperature field in the 2D model (40% load)
图5. 二维模型对应的温度场(40%负载)
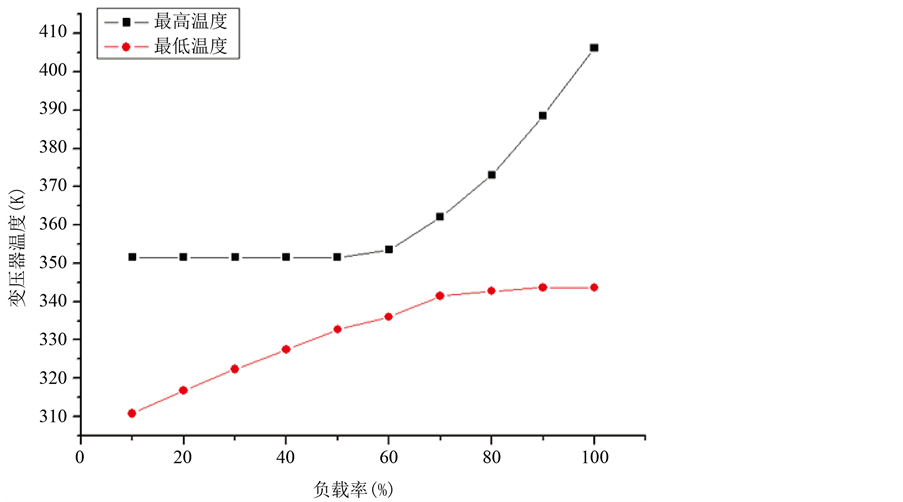
Figure 6. Transformer temperature curve with the load rate changes
图6. 变压器温度随负载率变化曲线
负载率为10%~50%之间时,变压器内部的最高温升都在铁芯处,且负载率每增加10%,在这个范围内,内部的最高温度值都保持在351.95 K,最低温度的增幅每次都为4 K左右。负载率超过60%的时候,最高温升开始增加,且增加的幅度随着负载率变大而变大,且变压器内部的最高温度点不再是铁芯处,而是在变压器的低压绕组处。在60%~90%之间,最低温度仍有一定的增幅,但是随着负载率的增加,增幅越来越小。负载率达到100%时,损耗最大,此时变压器整个的温升分布都达到最大值,最低温度的大小已不再变化。
4. 结论
根据10 kV干式变压器发热和散热的过程,建立了二维和三维模型,采用有限元法对温度场进行了数值计算与分析,可用于变压器的热特性分析、故障分析、稳定运行以及结构优化设计。得出结论如下:
1) 随着环境温度的升高,变压器的最高温度呈近似线性增加,外界环境温度每升高2 K,变压器的最大最小温度相应变大接近1 K的值;
2) 在负载率为0%~56%之间时,变压器的最高温度出现在铁芯,在这个范围内,负载率的提高对变压器的最高温度影响不大;之后随着负载率的提高,变压器的最高温度点出现在变压器低压绕组,变压器的最高温度随着负载率的提高而升高。
基金项目
重庆高校创新团队建设计划资助项目(CXTDX201601034);重庆市教委科学技术研究项目(KJ1710258)。