1. 引言
由于蜂窝夹芯结构有着轻质、高强度及良好隔声性能等特点,其广泛应用于航空、航天、汽车等结构中 [1] 。蜂窝夹芯结构根据芯格形状,可分为正六边形、方形、圆形、皱褶形材等蜂窝结构。工程常见的是传统正六边形蜂窝夹芯结构。
然传统正六边形蜂窝夹芯结构仍存在不足之处:如加工工艺复杂,存在尖角易产生较大的集中应力,加速了结构的疲劳损伤,降低了结构的稳定性。因此有人提出通过改变蜂窝夹芯胞元的形状来弥补传统蜂窝结构的缺点,比如采用圆形孔代替正六边形。相比正六边形蜂窝结构,主要特点是:圆形孔蜂窝结构夹芯耗材量少,比强度更高,承载能力更强,同时还可避免产生由于六边形孔角部应力集中而造成的结构裂纹、断裂、失稳等问题。针对蜂窝夹芯结构在力学、振动、声学、控制优化等方面的研究很多 [2] [3] ,如徐胜今等,利用等效理论对正交各向异性蜂窝夹层板的静、动力学问题进行了相关研究 [4] ;卢天健等,也从轻质蜂窝夹层板的制备方法到其振动、声学特性进行了深入研究 [5] [6] [7] ;王义柏等,利用有限元方法研究了单向加筋双层板的隔声性能 [8] 。蜂窝夹芯结构性能分析的关键就是建立结构模型,并得到相关结构的等效参数 [9] [10] [11] [12] ,如等效刚度及等效质量。而对圆形蜂窝的研究也有很多,有学者针对圆形夹芯蜂窝,基于有限元方法,研究了蜂窝结构参数与强度极限之间的关系 [13] ;针对圆形蜂窝夹芯板梁结构的临界应力进行了理论研究 [14] ,还有利用数值模拟软件来对圆形蜂窝的力学弹性参数进行了相关的研究 [15] 。
上述研究成果中多数是利用近似公式进行分析,但其存在一定应用范围。于是有必要对疏排圆形蜂窝结构的等效力学参数进行理论推导与求解,才能确定出一个近似数值范围,与数值模拟得到的结果进行比对分析验证。为此,本文提出一种新的思路,针对疏排蜂窝夹芯结构的等效模拟,通过建立半径为 、厚度为
、厚度为 、高度为
、高度为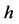 的圆形胞元的理论模型,结合其结构的受力特点,利用等效理论、结合力学等相关理论知识,得到其等效模型,对等效后模型的弹性力学参数进行推导。此研究为圆形蜂窝夹芯结构的发展提供了新的理论思路,具有重要的借鉴性意义。
的圆形胞元的理论模型,结合其结构的受力特点,利用等效理论、结合力学等相关理论知识,得到其等效模型,对等效后模型的弹性力学参数进行推导。此研究为圆形蜂窝夹芯结构的发展提供了新的理论思路,具有重要的借鉴性意义。
2. 疏排圆形蜂窝夹芯结构
疏排圆形蜂窝夹芯结构如图1所示,可以看出,圆形胞元均匀分布,彼此外切,每个圆形胞元周围对应有四个相同的圆形胞元与之相接触,这里用字母 、
、 、
、 来分别表示圆形夹芯的半径、壁厚、高度;从而有助于下一步的公式推导、计算。
来分别表示圆形夹芯的半径、壁厚、高度;从而有助于下一步的公式推导、计算。
3. 圆形胞元等效模型的建立
从蜂窝结构中取出一个单元,作为研究对象,即如图2所示,分析单元由五个圆形胞元组成,中心胞元与上下左右四个胞元所围成;该分析单元组成了整个蜂窝夹芯层结构。根据这五个圆形胞元接触特点,用直线将接触点相连,即组成一个规则的正方形等效模型。明显得到,疏排圆形夹芯层结构均可由这样的正方形胞元所围成,且满足两个基本等效要求:(1) 其面积和疏排圆形蜂窝面积相等;(2) 圆形胞
元间接触受力形式及受力方向,近似等同该正方形胞元的受力特性。
等效力学弹性参数推导
(1)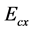 、
、 比的推导,首先建立如图所示直角坐标系,当蜂窝夹芯层受到
比的推导,首先建立如图所示直角坐标系,当蜂窝夹芯层受到 方向的单向应力
方向的单向应力 时,等效模型受力如图(a)所示,图(b)为等效模型中正方形胞元受力图,可以得到:
时,等效模型受力如图(a)所示,图(b)为等效模型中正方形胞元受力图,可以得到:

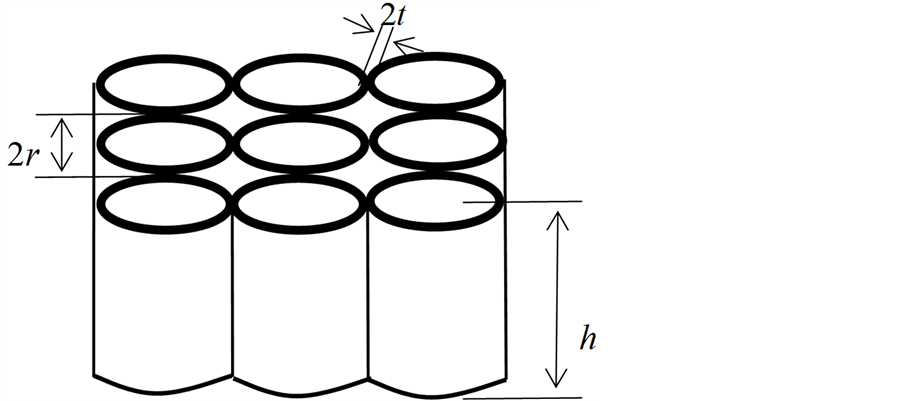
Figure 1. Circular honeycomb sandwich structure
图1. 疏排圆形蜂窝夹芯结构


由于结构在 点处的转角为0,据力学相关知识可得:
点处的转角为0,据力学相关知识可得:
 ,
,  ,
, 
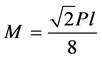
分别对模型中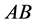 、
、 的轴向变形和弯曲变形进行分析,
的轴向变形和弯曲变形进行分析, 、
、 关于竖直方向对称,故有:
关于竖直方向对称,故有:
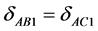 ,
,
 (
( )边由
)边由 力和弯矩
力和弯矩 所引起的垂直
所引起的垂直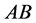 于方向的挠度为:
于方向的挠度为:
 ,其中
,其中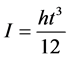 ;
;
 (
(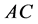 )的轴向变形为:
)的轴向变形为:
 ;
;
 方向的等效应变为:
方向的等效应变为: ;
;
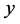 方向的等效应变为:
方向的等效应变为: ;
;
则 方向的
方向的 比和等效面内弹性模量为:
比和等效面内弹性模量为:
 ;
;
 ,这里
,这里 ;同理,可推出
;同理,可推出 和
和 的计算公式。
的计算公式。
(2) 、
、 比的推导,分析方法与上述类似如图(c)、图(d)所示,则有
比的推导,分析方法与上述类似如图(c)、图(d)所示,则有



 ,其中
,其中 ;
;
 ;
;
此时, 方向的等效应变为:
方向的等效应变为: ;
;
 方向的等效应变为:
方向的等效应变为: ;
;
则 方向的
方向的 比和等效面内弹性模量为:
比和等效面内弹性模量为:
 ;
;
 ,这里
,这里 ;
;
(3) 比的推导,等效模型的受力分析如图(e)、(f)所示,为满足各个节点受力平衡,
比的推导,等效模型的受力分析如图(e)、(f)所示,为满足各个节点受力平衡,
故做如下假设:
1) 假设A、B、C三个节点之间无相对位移;
2) 各节点转角相等;
3) 模型中每条边的剪切变形分别由其自身转动和弯曲变形所产生。


首先对节点 竖直投影到
竖直投影到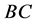 连线上的
连线上的 点取矩,有
点取矩,有 ,可得
,可得
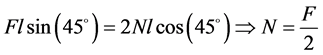
由图(e)中等效体剪应力互等定理可得

也可以推出 ;
;
图(g)取自于图(f)的左半部分,对 点取矩,
点取矩,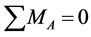 ,可得
,可得

 ;
;
故只有弯曲变形,则
 ;
;
 ;
;
所以有
 ,其中
,其中 ,则有
,则有
 ;
;
综上所述,可以看出结构面内力学参数:弹性模量 、泊松比
、泊松比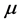 、剪切模量
、剪切模量 均与圆形胞元的厚度
均与圆形胞元的厚度 、半径
、半径 以及等效长度
以及等效长度 有关。在结构材料基本参数给定的情况下,利用得到的理论推导公式便可计算出疏排圆形蜂窝夹芯结构面内等效力学参数的近似值。
有关。在结构材料基本参数给定的情况下,利用得到的理论推导公式便可计算出疏排圆形蜂窝夹芯结构面内等效力学参数的近似值。
4. 数值模拟计算
取部分蜂窝夹芯层建立了 三维实体有限元模型,并设定结构为铝合金材料,为了方便载荷的施加,
三维实体有限元模型,并设定结构为铝合金材料,为了方便载荷的施加,

Figure 3. Three-dimensional finite element model
图3. 三维有限元模型图

Figure 5. Three-dimensional tensile deformation
图5. 三维拉伸形变图

Figure 6. Three-dimensional shear deformation
图6. 三维剪切形变图

Table 1. Comparison of theoretical and simulation values
表1. 理论值与仿真值比较
特在圆形夹芯左右两侧各添加一块薄板如图3,各圆形胞元间、薄板与胞元间均为固连形式,根据力的传递特性,这两块薄板不会对整体变形情况造成很大影响,故忽略不计;设置该模型网格类型为正六面体,网格尺寸0.5 mm,节点数353,465个,网格数75,484个,如图4。首先在模型的左侧设定一个固定端约束,右侧施加 方向均匀分布的拉应力,设定该拉应力为1 MPa,进行静力学分析,得到拉伸形变图5;接着在右侧壁板施加一个剪力,对模型产生一个
方向均匀分布的拉应力,设定该拉应力为1 MPa,进行静力学分析,得到拉伸形变图5;接着在右侧壁板施加一个剪力,对模型产生一个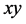 面内的侧向切应力,进行静力学分析,得出剪切形变图6。
面内的侧向切应力,进行静力学分析,得出剪切形变图6。
5. 理论结果与仿真结果对比验证
本文所建模型中,圆形胞元的内径14 mm,外径16 mm,故取半径r为7 mm,厚度为1 mm,高度h为8 mm,模型材料为铝合金,其弹性模量是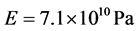 ,泊松比
,泊松比 ,通过拉伸、剪切实验测出疏排圆形蜂窝夹芯面内弹性模量及面内剪切模量,并进行结果对比分析见表1。
,通过拉伸、剪切实验测出疏排圆形蜂窝夹芯面内弹性模量及面内剪切模量,并进行结果对比分析见表1。
通过比较可以看出,本文的建模思路及理论推导方法与仿真实验数据结果偏差较小,从而验证该近似等效力学模型具有一定精度和合理性,理论结果的误差主要是等效近似所导致的,可根据具体实际问题进行合理范围内的修正,以达到较好的精度。
6. 结论
本文的创新之处是针对疏排圆形蜂窝板夹芯层面内等效力学参数计算问题,提出一种新的理论计算推导思路,得出的理论结果可以为仿真结果提供一个很好的参考。利用这种思路和方法,分别对其面内等效力学参数 、
、 、
、 、
、 、
、 进行了数值理论推导,并得到了各自的理论计算公式,以及圆形胞元的半径、厚度是影响该型蜂窝结构夹芯面内力学等效参数的主要因素的结果。
进行了数值理论推导,并得到了各自的理论计算公式,以及圆形胞元的半径、厚度是影响该型蜂窝结构夹芯面内力学等效参数的主要因素的结果。