1. 前言
活塞式压缩机由于活塞速度周期性的变化必然会产生往复惯性力,而旋转质量不平衡也会引起旋转惯性力。在多列压缩机中,由于曲拐不在同一平面上,还会存在惯性力矩。这些惯性力和力矩如果在机器内部不能完全平衡,必然会传到机器外部,引起机器的振动。振动不仅会消耗能量,影响压缩机的正常工作,还会影响到仪器仪表的寿命以及导致基础及建筑物的损害。严重时会引起机器的共振,毁坏设备或缩短使用寿命。
文献 [1] [2] 分别对三列立式压缩机和对置三列压缩机惯性力及力矩平衡及计算进行了详细的分析与研究,并且采用空间几何图形对其离心惯性力及力矩进行了分析。文献 [4] 对四列氮氢气压缩机惯性力平衡进行了分析与计算。
但现有的压缩机惯性力的研究中,往往仅仅针对不同类型、不同结构进行惯性力平衡研究。而多列压缩机由于列数较多,且气缸之间的夹角 不同、各列曲柄之间的错角
不同、各列曲柄之间的错角 不同、压缩机的旋转方向也不同,特别要使用空间图形表达离心惯性力及力矩的计算就显得更为复杂 [3] 。
不同、压缩机的旋转方向也不同,特别要使用空间图形表达离心惯性力及力矩的计算就显得更为复杂 [3] 。
惯性力计算中首先是各列的相位角难以确定,往往会在多列惯性力合力及合力矩分析中出现差错,特别在多列离心惯性力合力及合力矩的计算中又无法应用图形表达,所以给多列惯性力及力矩分析带来困惑。
本文针对多列往复惯性力、离心惯性力及力矩的特点,给出合成的规律,对于如何选取各列的相位角问题给出计算准则,特别对离心惯性力及力矩的合成给出计算方法。在活塞式压缩机中,由于多列切向力的合成方法与惯性力合成方法相同,所以此惯性力的合成方法也极易推广到多列压缩机切向力合成的计算中。
2. 多列惯性力合成的思路
压缩机惯性力的分析中,通常选取该列的外止点 时作为该列曲柄转角的起始点,气缸之间的夹角
时作为该列曲柄转角的起始点,气缸之间的夹角 和曲柄错角
和曲柄错角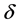 的存在,使得多列压缩机各列在同一瞬时的惯性力存在一定的相位差,惯性力的合成是在同一瞬时各列不同相位角的合成,只有确定各列之间的相位差,才能准确计算出多列压缩机的合成惯性力。
的存在,使得多列压缩机各列在同一瞬时的惯性力存在一定的相位差,惯性力的合成是在同一瞬时各列不同相位角的合成,只有确定各列之间的相位差,才能准确计算出多列压缩机的合成惯性力。
根据以上各列惯性力的特点和各列之间的相位差,多列惯性力合成时应遵守以下准则:
1) 先选定基准列,可以选择任一列,但通常以远离驱动侧一端的第一列作为基准列;
2) 确定各列曲柄转角间的关系。各列曲柄转角均从本列气缸中心线开始顺曲轴旋转方向到本列曲柄该瞬时所在位置的角度,设某一瞬时基准列的曲柄转角为 ,同一瞬时其余各列相应的曲柄转角分别为
,同一瞬时其余各列相应的曲柄转角分别为 。由于各列处于同一瞬时合成,即相对于基准列,将各列曲柄转角
。由于各列处于同一瞬时合成,即相对于基准列,将各列曲柄转角 表示成基准列曲柄转角
表示成基准列曲柄转角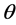 的函数;
的函数;
3) 确定往复惯性力的矢量方向。各列往复惯性力的方向均以本列指向外止点的方向作为正矢量方向,旋转惯性力沿着曲柄方向指向外为正矢量方向,并将各列的惯性力按此矢量方向合成。
本文以两列立式且曲柄错角 的压缩机为例,讨论惯性力与惯性力矩的合成,其多列压缩机惯性力及力矩的计算方法完全相同。图1表示了这种压缩机运动机构的简图:
的压缩机为例,讨论惯性力与惯性力矩的合成,其多列压缩机惯性力及力矩的计算方法完全相同。图1表示了这种压缩机运动机构的简图:
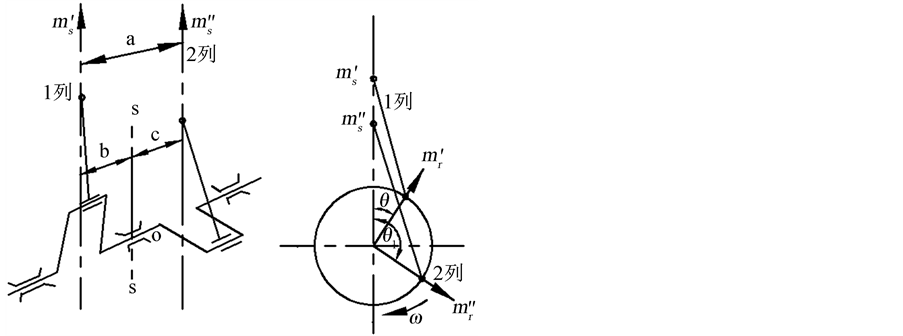
Figure 1. Two columns vertical compressor organization graph of crankshaft angle 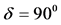
图1. 两列立式曲柄错角为 运动机构简图
运动机构简图
3. 惯性力的计算
根据牛顿定理,往复和旋转惯性力的一般表达式为:
 (1)
(1)
式中: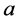 -活塞运动加速度(m/s2);
-活塞运动加速度(m/s2);
 、
、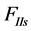 -分别为一阶和二阶往复惯性力(N);
-分别为一阶和二阶往复惯性力(N);
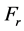 -旋转惯性力(N);
-旋转惯性力(N);
 -往复运动质量(kg);
-往复运动质量(kg);
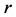 -曲轴的回转半径(m);
-曲轴的回转半径(m);
 -曲柄半径连杆比(即回转半径
-曲柄半径连杆比(即回转半径 与连杆长度
与连杆长度 的比值);
的比值);
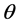 -曲轴的转角(˚);
-曲轴的转角(˚);
 -曲轴的旋转角速度(1/s);
-曲轴的旋转角速度(1/s);
在压缩机作用的分析计算中,一般规定使连杆受拉的力为正,受压为负。曲柄承受拉力为正,否则为负,这样式(1)中符号不再考虑。
根据式(1),当两列的曲柄夹角 时,二列的往复运动质量分别为
时,二列的往复运动质量分别为 和
和 ,而旋转质量为
,而旋转质量为 和
和 ,由相位角确定准则,取第一列为基准列,其曲柄的转角为
,由相位角确定准则,取第一列为基准列,其曲柄的转角为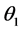 ,则同一瞬时第二列曲柄转角为
,则同一瞬时第二列曲柄转角为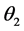 ,第二列与第一列转角之间的函数关系为
,第二列与第一列转角之间的函数关系为 ,则各列的一、二阶惯性力分别为
,则各列的一、二阶惯性力分别为
第一列
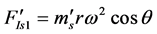 (2)
(2)
 (3)
(3)
 (4)
(4)
第二列
 (5)
(5)
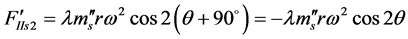 (6)
(6)
 (7)
(7)
将二列往复惯性力分别转化到质心平面 ,取二列的往复和旋转质量相同,即
,取二列的往复和旋转质量相同,即 ;
; ,其列间距
,其列间距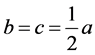 ,得到一、二阶往复惯性力的合力和合力矩:
,得到一、二阶往复惯性力的合力和合力矩:
由式(2)和式(5),两列一阶往复惯性力的合力为
 (8)
(8)
由式(3)和式(6),两列二阶往复惯性力的合力为
 (9)
(9)
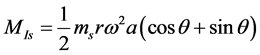 (10)
(10)
 (11)
(11)
而两列的旋转惯性力的相位角相差90˚,按照矢量合成的法则,旋转惯性力合力为
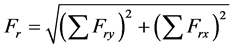 (12)
(12)
式中: —各列沿气缸中心线方向(垂直方向)的分力,其值为
—各列沿气缸中心线方向(垂直方向)的分力,其值为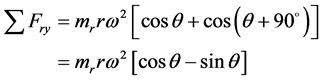
 —各列垂直于气缸中心线方向(水平方向)的分力,其值为
—各列垂直于气缸中心线方向(水平方向)的分力,其值为
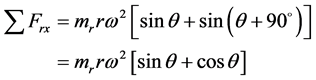
旋转惯性力的合力为
 (13)
(13)
旋转惯性的合力与Y轴的夹角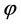 为
为
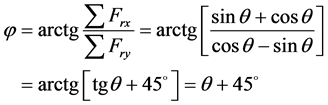 (14)
(14)
上式说明,此种结构的旋转惯性力的合力与Y轴的夹角恒较第一列曲柄超前450。
对于旋转惯性力矩,则先将每列的旋转惯性力投影到垂直轴Y和水平轴X,再对几何中心(S-S)求矩,两列分别在质心平面的两侧,即旋转惯性力的合力矩为:
在垂直平面内的旋转惯性力矩为
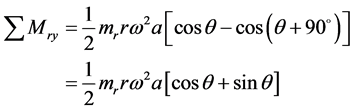 (15)
(15)
在水平面内的旋转惯性力力矩为
 (16)
(16)
旋转惯性力的合力矩为
 (17)
(17)
合力矩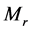 与垂直轴(气缸中心线平面内)的夹角为
与垂直轴(气缸中心线平面内)的夹角为
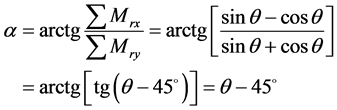 (18)
(18)
由此可见,对于两列立式且曲柄错角 的压缩机,其一阶往复惯性力和力矩以及二阶往复惯性力矩均无法平衡;二阶往复惯性力能自动平衡;旋转惯性力
的压缩机,其一阶往复惯性力和力矩以及二阶往复惯性力矩均无法平衡;二阶往复惯性力能自动平衡;旋转惯性力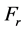 和旋转惯性力矩
和旋转惯性力矩 均为定值,其方向分别恒位于第1列曲柄超前和落后450,即在曲轴上加装平衡重即可平衡旋转惯性力和旋转惯性力矩。一阶往复惯性力和惯性力矩以及二阶往复惯性力矩均是随曲柄的转角周期性的变化,采用简单的方法无法平衡,由此可见,这种结构形式的压缩机惯性力平衡较差。
均为定值,其方向分别恒位于第1列曲柄超前和落后450,即在曲轴上加装平衡重即可平衡旋转惯性力和旋转惯性力矩。一阶往复惯性力和惯性力矩以及二阶往复惯性力矩均是随曲柄的转角周期性的变化,采用简单的方法无法平衡,由此可见,这种结构形式的压缩机惯性力平衡较差。
4. 结论
在多列活塞式压缩机中,由于各列气缸存在一定的夹角 ,各列曲柄也存在着一定的错角
,各列曲柄也存在着一定的错角 ,所以各列的惯性力便组成了一个空间力系,这就给多列惯性力的合成或叠加带来了一定的复杂性。利用论文所给出的惯性力合成准则,即可极为准确地确定各列之间的相位角,进而计算出多列压缩机的往复惯性力的合力及合力矩,特别对于多列的旋转惯性力的合力与合力矩无需应用图形的形式表示,提高了计算效率与准确性。本文以两列压缩机为例,详细介绍了两列往复压缩机往复惯性力合力和旋转惯性力合力及合力矩的计算方法,其计算结果与文献 [5] [6] 相同。论文虽然讨论了两列压缩机惯性力及力矩的计算步骤,但多列压缩机惯性力及力矩的计算完全相同,所以此方法易于推广到多列计算中,也为压缩机切向力的合成计算提供了参考。
,所以各列的惯性力便组成了一个空间力系,这就给多列惯性力的合成或叠加带来了一定的复杂性。利用论文所给出的惯性力合成准则,即可极为准确地确定各列之间的相位角,进而计算出多列压缩机的往复惯性力的合力及合力矩,特别对于多列的旋转惯性力的合力与合力矩无需应用图形的形式表示,提高了计算效率与准确性。本文以两列压缩机为例,详细介绍了两列往复压缩机往复惯性力合力和旋转惯性力合力及合力矩的计算方法,其计算结果与文献 [5] [6] 相同。论文虽然讨论了两列压缩机惯性力及力矩的计算步骤,但多列压缩机惯性力及力矩的计算完全相同,所以此方法易于推广到多列计算中,也为压缩机切向力的合成计算提供了参考。