1. 引言
煤矿瓦斯爆炸是煤炭开采过程中最严重灾害之一，尤其是特别重大瓦斯爆炸事故导致众多人员伤亡、巷道设施设备严重破坏和巨大财产损失，造成不良的社会影响。例如2004年大平煤矿、陈家山煤矿、2005年孙家湾煤矿、2007年山西瑞之源煤业公司等瓦斯爆炸事故。因此，我国政府加强了煤矿的安全投入和安全管理，在国有重点煤矿中，推行综合机械化开采技术，其比例己达75%，并出台和修订了一批强化安全管理的法律法规，如《煤矿安全规程》、《防治煤与瓦斯突出规定》等；同时，坚决关闭一些证件不全、非法开采的小煤矿，我国安全技术及管理水平得到了较大提高，我国煤矿生产安全状况持续好转，但也偶尔也发生了许多重特大瓦斯爆炸事故。国内外许多的专家学者利用实验巷道或管道平台对瓦斯爆炸进行了大量实验研究 [1] [2] [3] [4] [5] ，也有学者采用了数值模拟方法对瓦斯爆炸进行分析，并取得大量的研究成果 [6] [7] [8] [9] 。当整个巷道充满瓦斯或产生连续瓦斯爆炸，其爆炸破坏时间相对较长。在一些矿井，瓦斯爆炸产生的冲击波甚至通过井口破坏地面建筑物，伤害地面人员 [10] [11] [12] [13] ，所以人们历来十分关注巷道周围结构在冲击波载荷作用下的冲击破坏问题，并进行了大量的研究工作 [14] [15] [16] [17] 。但是采用数值模拟分析瓦斯爆炸热冲击问题时，不同瓦斯爆炸强度的管道壁面破坏特征分析较少。然而LS-DYNA能很好解决热冲击对管道壁面破坏问题，因此，本文利用LS-DYNA对管道内瓦斯爆炸热冲击进行了数值模拟，研究不同瓦斯爆炸强度的管道壁面冲击破坏特征，期望研究结果为煤矿或瓦斯隧道等受限空间的瓦斯爆炸事故防治以及降低瓦斯爆炸事故灾害损失提供理论依据和技术指导。
2. 物理数学模型的建立
2.1. 物理模型
2.1.1. 有限元模型的建立
本次所用材料的模型和参数均采用统一单位制(kg/m/s)，本次数值模拟所采用管道几何参数：管道长L = 20 m，半径r = 0.8 m，一端密闭，另一端为开口，预混气体与管道开口末端之间用膜片隔开，管道有限元模型如图1所示。
2.1.2. 网格划分
根据本次研究内容的需要，对于规则形状的管道模型，通常利用映射网格划分，对管道瓦斯爆炸物理模型采用六面体单元映射网格划分。因此，本次设置单元尺寸大小为0.04 m，管道瓦斯爆炸物理模型共划分为1,563,880个单元，管道的单元数为33,200个，瓦斯单元数为765,340个，空气的单元个数为765,340个，划分网格后的有限元模型如图2。
Figure 1. Finite element model of pipes
图1. 管道有限元模型
Figure 2. The finite element model after meshing
图2. 划分网格后的有限元模型
2.1.3. 定义单元类型与材料模型
利用ANSYS/LS-DYNA，采用8节点实体SOLID164单元建立管道瓦斯爆炸物理模型，根据国外现有的有关领域研究成果及研究现状可以知道，应变率是结构抗动态冲击荷载一个非常关键的因素。因此，材料模型应选用适用于钢材并考虑应变率影响的模型。本次选用非线性塑性材料模型，常用的模型为*MAT_PLASTIC_KINEMATIC，对于爆炸冲击荷载作用下的金属材料非常适用，其中，应变率采用Cowper-Symonds模型来考虑。
2.1.4. 边界条件与初始条件
瓦斯爆炸是一种极其迅速复杂的化学反应，其爆炸过程中所涉及大量的中间和瞬间产物，本次忽略其化学反应的中间过程。为了简化计算，对几何模型做出了一些基本假设如下：(1) 只有瓦斯爆炸热源存在，管道内再无其它热源。(2) 设置管道壁面光滑绝热，瓦斯初始状态如浓度、温度和压力均匀分布，初始温度和压力分别为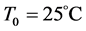
，
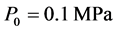。(3) 模型设置一端密闭，另一端开口且无反射边界条件。(4) 几何模型的轴对称性，边界的剖面法线方向位移为零。
2.1.5. 状态方程
瓦斯爆炸过程涉及许多的瞬间和中间产物，若不考虑热辐射、热传导、对流以及粘滞摩擦等，则将爆炸后生成的爆炸产物均可当作理想介质。瓦斯与空气的混合气体在爆炸过程中，其原始反应物和爆炸产物分别遵循理想气体的状态变化特性，因此，采用理想气体的γ律方程描述爆炸后的气体状态变化过程。
(1) 瓦斯材料模型及状态方程
LS-DYNA中采用HIGH_EXPLOSIVE_BURN材料关键字描述爆炸物质，同时结合线性多项式状态方程LINEAR_POLYNOMIAL进行相应定义。
(2) 空气材料模型及状态方程
空气一般采用空气材料模型和线性多项式状态方程加以描述，线性多项式状态方程为：
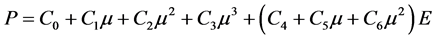(1)
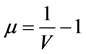
式中，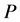
表示爆炸压力；
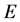表示单位体积内能；
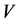表示相对体积。当此方程用于空气模型时：
，
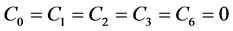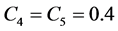。空气密度为1.225 kg/m3，初始相对体积
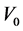为1.0。
2.2. 数学模型
2.2.1. 基本假设
为了方便数值模拟和建立数学模型，本次进行如下假设：① 不考虑瓦斯的化学反应过程，但需要考虑气体粘性。② 假设管道绝热、光滑，常温常压下瓦斯预混气体初始状态如浓度、温度和压力分布均匀。
2.2.2. 基本控制方程
管道瓦斯爆炸传播问题属于一端开口、一端封闭的管状空间内含有高温高压的冲击波流动过程，在直角坐标系下，瓦斯爆炸流场三维非定常流动的三个守恒方程式分别如下：
质量守恒方程：
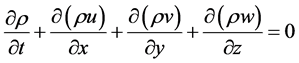(2)
动量守恒方程：
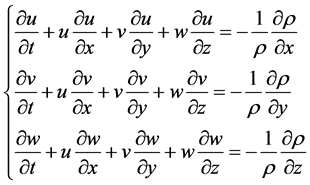(3)
能量守恒方程：
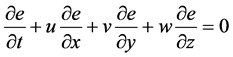(4)
状态方程：
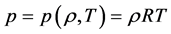(5)
式中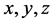
为坐标参数；
为流体密度，kg·m−3；
为压力，Pa；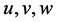
分别是三个坐标方向的速度，
；t为时间坐标，T为温度，K；R为气体常数；
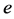为比能，
，
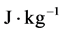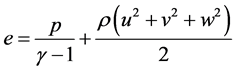，其中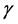
是气体指数，为常数。
3. 数值模拟及结果分析
通过管道内瓦斯填充长度的不同来实现瓦斯爆炸的不同强度，进而研究不同的瓦斯爆炸强度对管道壁面损伤破坏的影响，基于前期分析结果和模拟结论，本次分别模拟了瓦斯填充长度为15 m、16 m、17 m、18 m、19 m和20 m。
图3是瓦斯填充长度为15 m的管壁不同时刻等效应力云图，从图3的分析可知，在0~0.04 s时间内，仅t = 0.01 s时刻，管壁最大值应力为279.3 MPa，管道局部位置应力超过了管道的屈服强度，管道发生了弹塑性变形，在0.01 s之后时间内，最大应力值均未超过279.3 MPa，未超过材料的抗拉强度，管壁瓦斯爆炸完成后，管道内还剩有空气冲击波作用，管壁再次发生变形，从瓦斯爆炸开始到完成整个时间内，管壁发生着变形-恢复循环往返，导致管道发生疲劳损伤，若冲击波持续加载，最终管壁会出现破坏现象。
图4为管道内填充长度为16 m的管壁不同时刻等效应力云图，从图4分析可知，在0~0.04 s的时间内，仅t = 0.01 s时刻，应力最大值为229.0 MPa，未超过管道屈服强度，管道发生了弹塑性变形，随着瓦斯爆炸的完成，瓦斯量的消耗，之后的整个时间内，最大应力都没有超过229.0 MPa，壁面没有出现破坏现象，但是管道会发生疲劳损伤效应。
图5是管道内瓦斯填充长度为17 m的不同时刻壁面等效应力云图，由图5分析可知，瓦斯爆炸瞬间，封闭端隅角处冲击波汇聚叠加，致使管道封闭端和管道发生膨胀变形。在t = 0.0008 s时，管道封闭端拐角位置沿圆的周向开始出现“Z”型缺口，即内壁面出现一层壁面失效，管道外壁没有任何的破坏痕迹。随着瓦斯爆炸的进行，爆炸冲击波压缩临近的气体，迫使周围的空气离开原来占据的位置，迅速向开口端运动。此时封闭端区域内出现了负压区，空气回流压缩，冲击波都汇聚在“Z型”槽里，冲击波叠加程度更大，封闭端膨胀再次发生变形，管壁又有一层的失效，管道壁面变薄，在“Z”型槽内壁面继续失效破坏，出现了“阶梯式”破坏特征。
图6为管道内瓦斯填充长度为18 m的不同时刻壁面等效应力云图，由图6分析可知，瓦斯爆炸瞬间，爆炸冲击荷载加载在管道壁面及封闭端，封闭端隅角处冲击波汇聚叠加，致使管道封闭端和管道发生膨
胀变形。在t = 0.0008 s时，管道封闭端与壁面的拐角区域沿圆的周向开始出现“Z”型缺口，管道外壁没有出现破坏痕迹。管道封闭端发生瓦斯爆炸，冲击波沿程衰减，导致封闭端区域内出现负压区，空气回流压缩，冲击波都汇聚在“Z”型槽里，冲击波叠加程度更为严重，出现了“阶梯式”破坏特征，其产生的原因是壁面反射冲击波、隅角汇聚冲击波及静态气体压力，其中壁面和封闭端结合处角隅汇聚冲击波最大。
图7为管道内瓦斯填充长度为19 m的不同时刻壁面等效应力云图，由图7分析可知，管道内瓦斯爆炸的瞬间，冲击荷载作用在管道封闭端及壁面上，封闭端隅角处冲击波汇聚叠加，致使管道封闭端和管道发生膨胀变形。t = 0.0008 s时，管道封闭端隅角沿圆的周向开始出现“Z”型缺口，管道外壁没有出现破坏痕迹。管道封闭端发生瓦斯爆炸，冲击波沿程衰减，导致封闭端区域内出现负压区，空气回流压缩，冲击波都汇聚在“Z”型槽里，冲击波叠加程度更为严重，出现了“阶梯式”破坏特征。
图8为管道内瓦斯填充长度为20 m的不同时刻壁面等效应力云图，由图8分析可知，瓦斯爆炸瞬间，管道壁面及封闭端受到爆炸冲击波直接加载，在管道隅角处冲击波汇聚叠加，致使管道封闭端向外膨胀变形。在t = 0.0008 s时，管道封闭端与壁面的拐角位置沿圆的周向开始出现“Z”型缺口，即内壁面出现一层壁面失效，此时管道外壁没有出现任何的破坏痕迹。随着瓦斯爆炸进行，爆炸冲击波压缩临近的气体，迫使周围空气离开原来占据的位置，迅速向开口端运动。此时封闭端区域内出现了负压区，空气回流压缩，冲击波都汇聚在“Z”型槽里，冲击波叠加程度更大，封闭端膨胀再次变形，在“Z”型槽内壁面再次失效，出现了“阶梯式”破坏特征，其产生的原因是壁面反射冲击波、隅角汇聚冲击波及静态气体压力，其中壁面和封闭端结合处角隅汇聚冲击波最大。
通过对管道内瓦斯填充长度分别为15 m、16 m、17 m、18 m和20 m的瓦斯爆炸对管道壁面破坏模式及特征进行了分析，由此可以得到：管道内瓦斯填充15 m和16 m时管道壁面没有出现明显的破坏，
但管道一定会出现疲劳损伤，若冲击波对管道壁持续作用，管道最终出现破坏。当管道内瓦斯填充长度17 m时，瓦斯爆炸瞬间管道壁面开始出现破坏现象，并且瓦斯填充长度超过17 m的管道壁面均出现了破坏，随着瓦斯填充长度的增大，管道壁面的破坏现象加剧。
随着管道内瓦斯填充长度增加，即瓦斯爆炸强度的增加，管道封闭端最开始有弹性膨胀变形，爆炸冲击波荷载超过了材料的屈服强度，管道封闭端与内壁面结合隅角部位，内壁面沿管道周向出现一层脱落，出现了“Z型”破坏，随着爆炸荷载的持续加载，壁面最终出现了“阶梯式”的破坏，但是爆炸强度继续增大，最终在管道壁面沿周向出现一圈缺口，封闭端逃离束缚，管道壁面开始撕裂，产生了张开型的扩展现象。
4. 结论
通过有限元软件LS-DYNA对管道内不同爆炸强度的瓦斯爆炸冲击破坏特性进行了数值模拟研究，得到如下结论：
(1) 在瓦斯爆炸瞬间，爆炸冲击波直接加载在管道壁面及封闭端，封闭端隅角处冲击波汇聚叠加，致使管道封闭端和管道发生膨胀变形。
(2) 随着瓦斯爆炸的进行，爆炸冲击波压缩临近的气体，迫使周围的空气离开原来占据的位置，迅速
a) 管道不同时刻的等效应力云图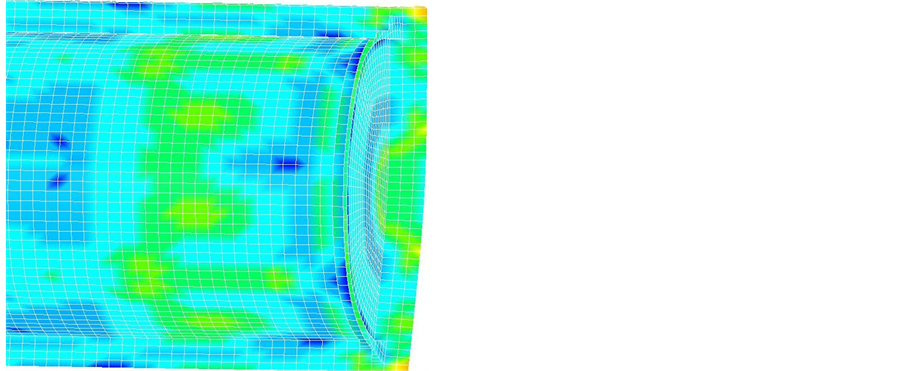
b) 局部放大图
Figure 8. The equivalent stress contour with gas filled length of 20 m in the pipe at different times
图8. 管道内瓦斯填充长度为20 m壁面等效应力云图
向开口端运动。此时封闭端区域内出现了负压区，空气回流压缩，冲击波都汇聚在“Z型”槽里，冲击波叠加程度更大，封闭端膨胀变形，管壁又有一层的失效，管道壁面变薄，出现了“阶梯式”破坏特征。其中壁面和封闭端结合处角隅汇聚冲击波最大。
(3) 随着瓦斯爆炸强度的增加，管道封闭端最开始有弹性膨胀变形，当爆炸冲击波荷载超过了材料的屈服强度，在管道封闭端与内壁面结合隅角部位的内壁面沿管道周向出现一层脱落，出现了“Z型”破坏。
(4) 随着爆炸荷载的持续加载，壁面最终出现了“阶梯式”的破坏。随着爆炸强度继续增大，管道壁面开始撕裂，产生了张开型的扩展现象。
基金项目
国家自然科学基金资助项目(51374003, 51004048, 51604110)，湖南省自然科学基金项目(2016JJ6038)，湖南省教育厅项目(E51523)。