1. 引言
全息的概念是1948年由英国的伽伯提出 [1] 。光学全息成像是利用光的干涉和衍射原理将物体反射回来的光波以干涉条纹记录下来，在一定条件下还原物体原有的立体像，全息成像技术与显微技术的结合形成全息显微技术 [2] ，利用显微技术将全息技术应用到微观测量领域。对全息图采样后对其进行再现算法，菲涅耳全息图的显微成像 [3] 对像的再现提出一个新的要求。近年来，随着利用计算机对全息图处理的数字全息 [4] [5] [6] 的问世，数字全息显微技术 [7] [8] [9] [10] 得到进一步的发展。然而，在全息图再现算法中，菲涅耳再现算法具有一定的缺点，针对像素大小不仅仅取决于像素个数M，N，CCD像素尺寸，还与再现距离
和波长
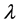有关的问题，研究者采用卷积再现算法来提高像素质量。讨论菲涅耳近似再现算法与卷积再现算法的优缺点。指出卷积再现算法解决的实际问题。
2. 数字全息的记录与再现
2.1. 数字全息记录
图1所示为数字全息记录原理图。在全息记录过程中，利用干涉原理记录物体光波信息，实现对物光信息的采集。如图1所示，一束激光出射后经过分光镜分成两束，一束光入射到样品表面，经样品表面调制后形成物光波，另一束光经过平面反射镜反射后形成参考光。物光波和参考光在CCD上形成干涉图，该干涉图即为全息图。在全息图中，不但包括物光波的振幅信息，也包括物光波的位相信息。
数字全息图的再现过程可以全部在计算机中通过数值计算来实现，而再现过程的本质就是利用计算机数值模拟再现光波照明记录的全息图并衍射传播的过程。如图2所示，物平面到全息平面是干涉过程，全息平面到像平面是衍射过程。常用的衍射传播方法大致可以分为三类：菲涅耳变换法(Fresnel Transform Method—FTM)、卷积法C Convolution Method—CVM)和角谱法(Angular Spectrum Method—ASM)。
CCD记录平面上的光强分布为：
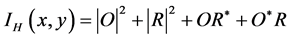(1)
经CCD抽样离散处理后的光强为：
(2)
其中
为CCD的光敏面大小，
为像素大小，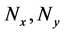
为像素数。
2.2. 数字全息再现
在数字全息中，全息图可看作一孔径，物光波的重现就是参考光波经过孔径衍射的结果。
当用相干光波照射全息图时，衍射光波可近似用菲涅耳–基尔霍夫积分表示：
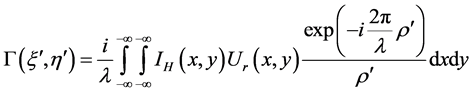(3)
其中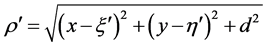
是全息图平面上的点到重建平面的点的距离，
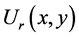是参考光波。把
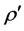右边按泰勒级数展开并取前两项，这时
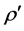可近似为：
Figure 1. Digital holographic optical system
图1. 数字全息系统光路
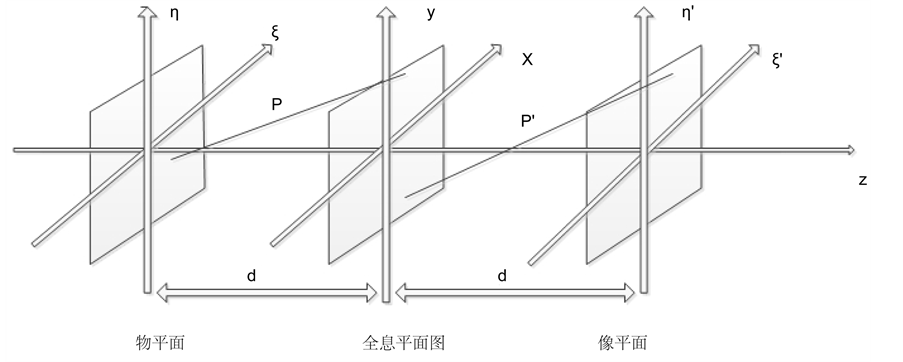
Figure 2. Schematic diagram of digital holographic
图2. 数字全息原理图
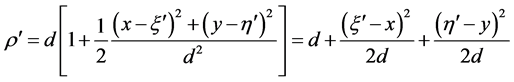(4)
由于坐标
及
远远小于距离d，式(3)中的分母
用d代替，再把式(4)代入，可以得到：
(5)
令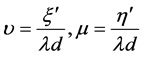
，式(5)离散化后为
：
(6)
其中
。式(6)为离散傅里叶变换，在菲涅耳近似算法中只用了一次快速傅里叶变换，如果我们把全息图平面所在的坐标看作空域坐标，那么重建像平面则位于空间频率域，会使得重建图像的像素大小改变，重建图像的像素大小由重建距离和所用波长决定：
(7)
然而卷积法是对空间衍射传播的一种精确描述，它主要是通过瑞利一索末菲衍射积分公式得到的，全息图经再现光波照明后传播到成像平面的光场的复振幅表示为，
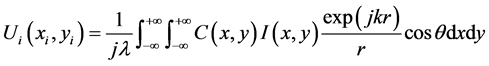(8)
其中
为成像平面坐标
为全息图记录平面坐标，
(9)
代表再现照明光波，Zi为衍射传播的距离即是再现距离，
表示波长，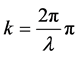
。
衍射积分的过程可以看作是物光波函数与脉冲响应的卷积，这个脉冲函数的响应也就是我们所说的卷积和函数，
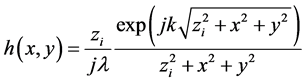(10)
将式(9)带入式(8)可得，
(11)
利用傅里叶变换性质，式(9)可表示为，
(12)
式中F.T.{}和F.T {}分别代表二维傅里叶变换。式(11)即为卷积算法的表达式，它需要完成三次傅里叶变换:此外，卷积的输入面与输出面上的采样间隔不发生变化，因此在现象面上的采样间隔等于CCD采集全息图的采样间隔。
3. 实验研究
使用波长为633 nm的激光；选用CCD型号：DMK42AUC03，像素：1280×960，像素尺寸：水平3.75 mm，垂直：3.75 mm，选取的光栅是在放大倍率为10倍的电子显微镜下观察的光栅结构如图3所示。在CCD记录感光面前方与被测件正交光栅间夹装显微物镜，正交光栅结构被显微物镜放大后光路通向CCD，
Figure 3. The structure of the orthogonal grating observed under the microscope
图3. 显微镜下观察的正交光栅结构图
在CCD感光面物光与参考光产生干涉。
对如图3所示的光栅结构进行显微全息记录。记录所得的全息图如图4所示，频谱图如图5所示。
在全息图中，可以看到有明显的干涉条纹存在，这些干涉条纹中记录了正交光栅对测试光的位相调制信息，也就是说正交光栅反射表面的高度信息反映在干涉条纹中。在频谱图中，可以清楚看到在三个区域出现亮斑，其中位于中心区域的为0级频谱，包含着全息图中的背景信息，位于上下区域的两个亮斑区域分别对应+1和−1级频谱，分别包含有测试光信息和测试共轭光信息，对频谱图中的+1级频谱进行选择并移到中心，再经过再现算法生成两者的相位图如图6和图7所示，相位图为解包裹后的相位图。在
Figure 6. Phase diagram of Fresnel representation
图6. 菲涅尔再现相位图
Figure 7. Phase diagram of convolution integral
图7. 卷积积分相位图
两个相位图中，可以看到，相对于菲涅耳再现相位图，卷积积分相位图在细节结构上更加清楚，过渡部分更加平滑，可以得到更好的测量结果。
采用菲涅尔再现算法，得到正交光栅结构的三维轮廓图如图8所示；采用卷积再现算法，得到正交光栅的三维轮廓如图9所示。通过对图8和图9的比较，可以看出，卷积积分得到的再现结构更加清楚，再现的光栅结构更加有序，这说明了卷积积分算法在再现过程中对于局部异变点的干扰具有更好的抑制作用。分别在选取线段截取表面三维轮廓的表面形态如图10和图11所示，从截面图上可以看到，两种再现算法均可以再现出光栅表面的正弦结构，两者在PV值和栅距上基本相当，但在细节表现力上卷积积分再现具有更好的效果。
通过对实验现象的观察，菲涅尔再现算法得到的再现图与卷积再现算法得到的再现图可以更为直观的了解到全息成像记录再现的这一过程，充分说明了计算机全息的优势。大大加大了我们对记录事物方式的转变和从时域到空间域飞跃。虽然菲涅尔、卷积积分再现算法能够再现正交光栅的结构，但是会受到技术、环境、算法等因素的影响，取得的再现像与正交光栅的原像存在这差别。在波长、CCD感光面一定的情况下使用菲涅耳再现算法时像素大小受到再现距大小的影响。充分说明卷在卷积算法中，根据
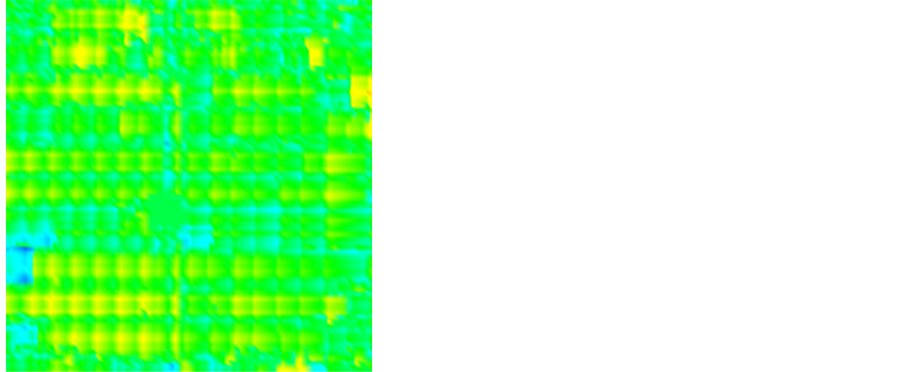
Figure 8. The result of Fresnel representation
图8. 菲涅尔再现结果
Figure 9. The result of convolution integral
图9. 卷积再现结果
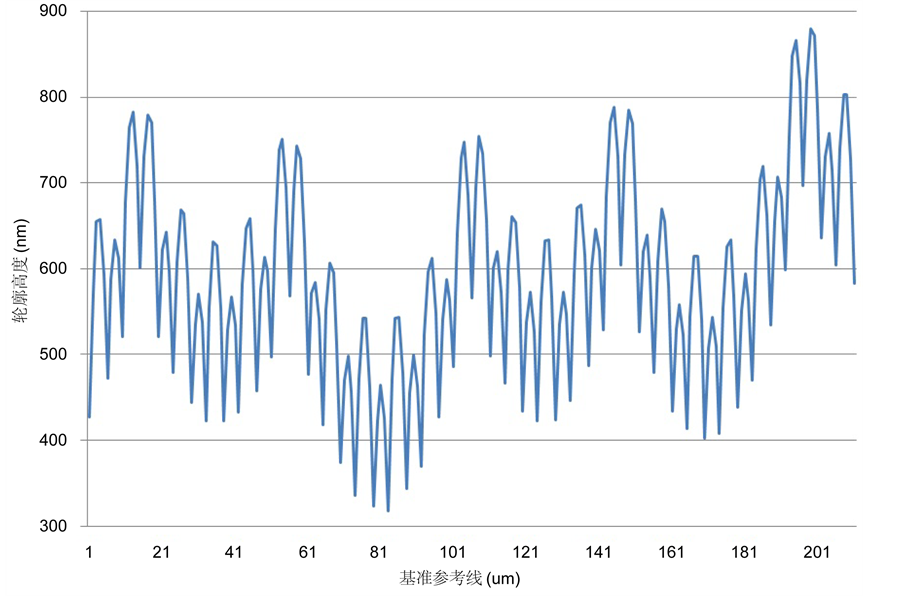
Figure 10. The sectional drawing of Fresnel representation
图10. 菲涅尔再现截面图
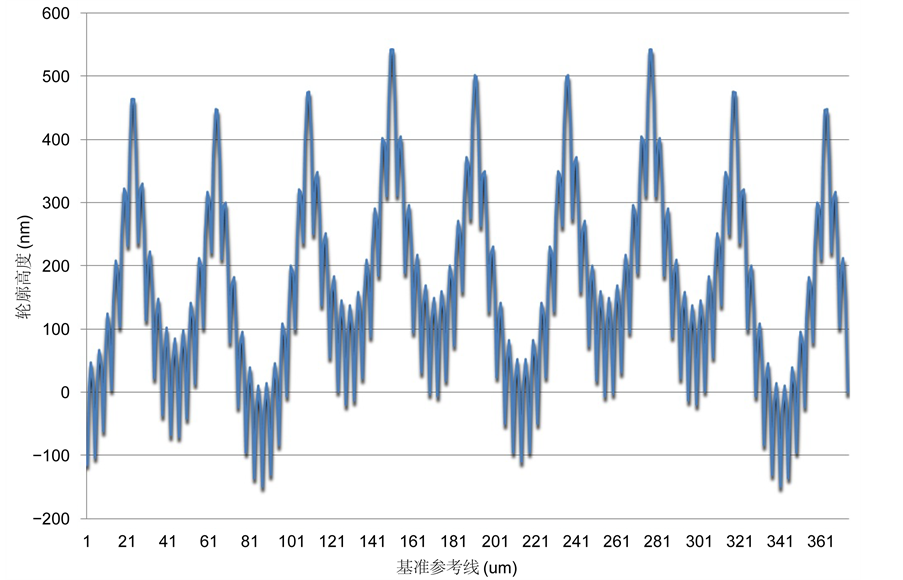
Figure 11. The sectional drawing of convolution integral
图11. 卷积积分再现截面图
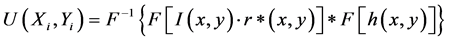，对全息图和脉冲响应分别作傅里叶变换，从空域变换到频域，在频域中全息图的傅里叶变换和传递函数相乘，接着做逆傅里叶变换又回到空域。得到再现像
的像素尺寸和CCD的尺寸大小就保持一致：
并且再现视场的大小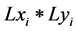
也是相同的。即使每次选择的再现距离
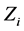不同，像素的大小依然不变。菲涅耳再现算法与卷积再现算法两者同时表明再现像的算法对于显微器件的测量具有可行性和有效性。
4. 结论
数字全息显微术在显微测量方面具有其他测量所不具备的优势，具有较高的分辨率，非接触，无损伤的特点，从光波的标量衍射理论出发，分析了数字全息的记录和菲涅耳、卷积积分再现原理的过程，检验了卷积积分再现算法的正确性、优越性，验证了数字全息显微成像技术用于微器件几何参数测量的可行性和有效性。通过对菲涅耳再现算法和卷积再现算法的比较研究，可以看出卷积再现算法得到的的再现结构更真实，卷积相位图更能表达结构特性。
资助信息
国家级大学生创新创业训练计划项目(项目编号：201610702037)；西安工业大学大学生创新专项经费资助项目。