摘要:
本文将多元函数的求导法则进行了归纳总结,通过画树形图得到求导的计算公式,并举例说明树形图法在求多元抽象函数偏导时的应用。
Abstract:
This article has carried on the induction summary of multivariate function derivative method, the derivation of the formula is obtained by drawing tree diagram, and illustrates tree diagram method in multivariate function abstract application of partial derivatives.
1. 引言
高等数学教学中多元函数微分学的内容是微积分的重要组成部分,尤其是多元复合函数偏导的求法是多元函数微分法及其应用这一章的重点和难点,它是微分学应用的基础。然而多元函数由于其情况比较复杂,自变量和中间变量不止一个,还会出现有些变量既是中间变量又是自变量的情形,因此学生在学习这节内容时仅靠死记硬背公式很难正确的解决这类问题。本文主要是结合教学,介绍一种在求多元复合函数的偏导数时非常实用的一种方法——画树形图的方法,并且这种方法在求多元抽象函数的偏导数时也是非常实用的。
2. 多元复合函数的求导法则
定理1 [1] 设函数 ,
, 在点
在点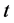 可导,
可导,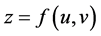 在点
在点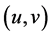 处偏导连续,则复合函数
处偏导连续,则复合函数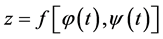 在点
在点 可导,且有全导数
可导,且有全导数

证明设 取增量
取增量 ,
, ,
,
由于 在点
在点 处偏导连续,则函数
处偏导连续,则函数 可微,
可微,
则 ,
,
因为
所以 。
。
分析:此公式可通过画树形图(如图1所示)帮助记忆,分段用乘,分叉用加。
这里是 中间变量,
中间变量,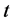 是自变量,
是自变量, 是因变量。
是因变量。
从树形图中可看到从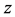 到的
到的 路径有两条,一条是从
路径有两条,一条是从 到
到 到
到 ,一条是从
,一条是从 到
到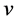 到
到 ,结合图形,可得到全导数的计算公式
,结合图形,可得到全导数的计算公式
推广:假设下面所涉及的函数均可微。
1) 中间变量多于两个的情形(图2所示)。
 ,
,  ,
,  ,
, 
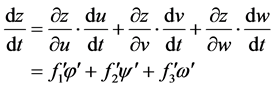
注: 表示
表示 对第一个位置上的函数求偏导。
对第一个位置上的函数求偏导。
2) 中间变量是多元函数的情形(图3所示)。
 ,
,  ,
,  ,
,
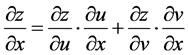 ,
, 
3) 中间变量同时又是自变量的情形(图4所示)。
 ,
, 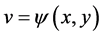 ,
,
 ,
, 
注: 与
与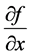 不同,
不同,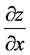 是固定
是固定 对
对 求导,
求导, 固定
固定 对
对 求导。
求导。
3. 多元抽象函数的偏导
求复合函数的偏导数是本节的难点和重点,特别是抽象复合函数的高阶偏导,一般采用链式法则 [2] ,另外要注意多元复合函数的求导法则的运用要具备一定的条件,如函数具有连续偏导数等。多元抽象函
数的偏导数在教学中是一个难点,尤其是多元抽象函数的高阶偏导数,学生不容易掌握,但是通过画树形图 [3] ,可以帮助学生理解抽象函数偏导的求法,计算中不容易出错。下面举例说明多元抽象函数求偏导的方法。
例设 ,
,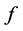 二阶偏导连续,求
二阶偏导连续,求 ,
, 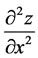 ,
, .
.
解
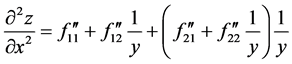


图5中的1,2分别表示 中第一个位置上的元素及第二个位置上的元素。
中第一个位置上的元素及第二个位置上的元素。
计算时要分清复合结构 [4] ,按结构顺序求一阶偏导和二阶偏导,特别在求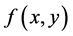 的二阶偏导时要注意
的二阶偏导时要注意 和
和 仍是
仍是 的函数。
的函数。
4. 总结
多元复合函数求偏导时可参照本文所列各种情形,先画出多元函数复合的树形图,再根据图形列出相应的公式,最后进行计算即可。
基金项目
2016年度河西学院教学改革基金项目“工科类高等数学教学改革研究”(项目编号:HXXYJY-2016-027)。