1. 引言
目前，我国已投运云广、复奉、锦苏、溪浙、哈郑、宁绍等特高压直流工程，出现多回直流密集馈入长江三角洲和珠江三角洲地区的情况。未来几年，在华北地区也会陆续投运多条特高压直流，届时，我国东部地区将形成多个容量巨大、结构复杂的多直流密集馈入受端系统。多馈入受端系统的直流落点近，交直流系统间和直流子系统间的相互作用强，系统电压稳定问题远较纯交流系统和单馈入系统更加突出和复杂 [1] [2] [3] [4] 。当受端交流系统较弱的情况下，电压稳定问题将成为电网运行面临的主要威胁 [5] 。
在多馈入交直流受端系统电压稳定方面还未形成成熟的指标体系，现有的最广泛应用的多馈入静态电压稳定评价指标为多馈入短路比指标(MSCR)。多馈入短路比是基于多馈入受端系统经多端口戴维南等值后的简化模型提出的，其各直流馈入之间的互阻抗使得多馈入短路比计算中需考虑其余各条直流馈入的影响 [6] [7] [8] 。另外多馈入短路比指标与静态电压稳定性的对应关系欠清晰，物理意义不很明确，因此找到一种新的多馈入静态电压稳定评价指标是非常必要的。
本文在传统多馈入受端简化模型的基础上通过对交流受端节点阻抗矩阵的对角化得到各特征值，提出了新的多馈入受端系统解耦模型，分析了各特征值的物理意义并根据解耦模型提出了新的多馈入电压稳定评价指标。对两个简单三馈入系统分别计算新指标值，在BPA软件中进行故障仿真对比两个系统故障后的系统电压稳定性，验证了新指标的可行性和实用性。
2. 多馈入受端交流系统的解耦
目前研究多馈入交直流系统的受端静态电压稳定常应用的模型是受端交流系统通过多端口戴维南等值后的系统简化模型 [9] ，如图1所示。
由于多条直流馈入之间有互阻抗的联系使得受端电压稳定的研究比单馈入系统复杂得多，因此，寻找一种更为简化的模型十分必要。由于静态电压稳定分析忽略交直流系统的动态过程，整个系统可简化为纯代数方程，因此可以在原有的模型基础上进行线性变化 [10] [11] 。
Figure 1. Traditional simplified model of multi-infeed HVDC system
图1. 多馈入交直流系统戴维南等值简化模型
在图1中，假设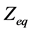
为从各回直流换流器母线处看进去的交流系统的等值节点阻抗矩阵，在包含
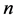回直流的多馈入交直流系统中，各回直流注入交流系统的电流分别为
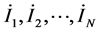，则可列出交流等效发电机端各点电压和交流母线节点电压之间的关系式为：
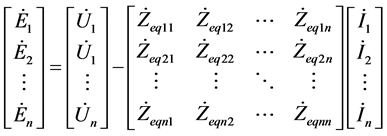(1)
在(1)中对等值节点阻抗矩阵进行对角化，设：
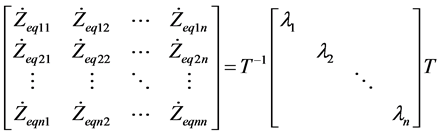(2)
其中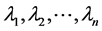
为等值节点阻抗矩阵的特征值，
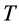矩阵为各特征值对应的特征向量组成的矩阵。
将式(1)左乘矩阵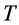
可得：
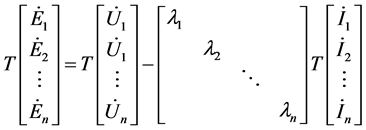(3)
在式(3)中令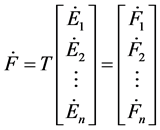
作为新的等效解耦系统的交流母线节点电压；
令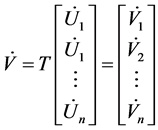
作为解耦系统的交流侧发电机节点的电压；
令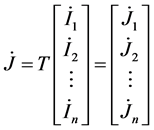
作为解耦系统的直流换流器注入交流系统的电流；
则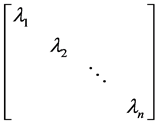
为等效解耦系统中交流侧各线路的等值阻抗。等效后的各条直流馈入的交流侧等
值阻抗为原受端系统等值阻抗矩阵的各特征值，等效系统模型如图2。
由图2可看出在多馈入系统解耦后的简化模型中，原阻抗矩阵的各个特征值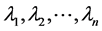
为解耦后每条单馈入受端系统的等值阻抗，原系统等效为多个单馈入系统，以电压最薄弱的那条单馈入馈入直流来作为原多馈入系统电压稳定的衡量标准。
3. 多馈入系统静态电压评价新指标
多馈入系统的静态电压稳定的判定方法大多都是将单馈入交直流系统的研究方法推广到多馈入系统中。静态电压稳定的分析忽略了交流和直流系统的动态过程，整个系统简化为线性系统。已有的多馈入系统静态电压稳定评价指标应用最广泛的为多馈入短路比指标，但多馈入短路比物理意义较为模糊，与多馈入系统静态电压稳定的对应关系不清晰 [12] [13] ，因此有必要研究并提出一种新的多馈入系统静态电压稳定评价指标。在图2所示的解耦模型中，多馈入系统被等效为多个单馈入系统，因此可以用单馈入系统静态电压稳定的研究方法来分析多馈入系统。将单馈入系统的受端系统通过戴维南等值简化 [14] [15] ，若假定受端换流母线电压恒定，负载用恒定阻抗表示，单馈入交直流系统可简化如图3所示的模型。
受端换流母线电压和交流负载节点的电压关系为：
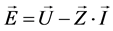(4)
负载节点功率计算式为：
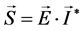(5)
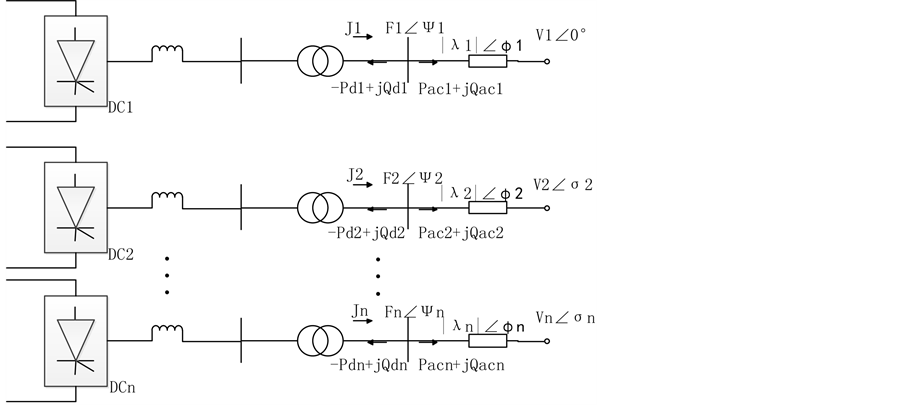
Figure 2. Decoupling model of multi infeed HVDC system
图2. 多馈入交直流系统解耦后的模型
Figure 3. Equivalent model of single infeed HVDC system
图3. 单馈入交直流系统等效模型
若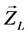
为负载阻抗，正常情况下，交流受端通过减小负载阻抗以求获得更大的功率需求，当负荷阻抗减小到和戴维南等值阻抗一样大时，系统不能再通过减小负荷阻抗以获取更大的功率，此时电压失稳 [16] [17] 。根据文献 [18] 电压稳定预测器的预测方法介绍可知当受端负载阻抗减小到跟戴维南等值阻抗一样大(
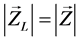)时，负载节点电压失稳。由此可见单馈入系统中戴维南等值阻抗对受端交流负荷节点的静态电压稳定起到关键作用，可以把戴维南等值阻抗的大小作为静态电压稳定的评价指标，通过比较负荷阻抗和戴维南等值阻抗的大小可以判断系统静态电压稳定性，戴维南等值阻抗越小说明负荷达到稳定极限的裕度越大，系统静态电压稳定越好。
图2所示的解耦模型把各回直流馈入有相互影响的多馈入系统等效为多个单馈入系统，受端系统等值阻抗矩阵对角化后的各个特征值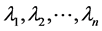
即为每条单馈入系统对应的交流受端的等值阻抗
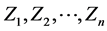，对于一个多馈入直流系统，在图2所示的多馈入解耦模型中，若定义戴维南等值阻抗最大值即最大特征值
为多馈入系统静态电压评价的新指标，最大特征值的值
越大，说明多馈入系统静态电压失稳的可能性越大。
4. 仿真计算
在BPA软件中搭建两个结构相同的三馈入系统模型算例A和算例B，电气接线图如图4。
对于这两个算例，将送端系统等值为三台无穷大的发电机，受端系统发电机用次暂态参数模型来表示，三台发电机的次暂态电抗都为0.01 p.u，不计励磁调节系统和调速器的作用。
在本算例中以230 kV为电压基准值，100 MW为功率基准值，所有参数均以标幺值计算。算例A和算例B的直流系统参数和交流系统参数及潮流数据见附录A和附录B。
利用多端口戴维南等值方法求取系统的短路阻抗。发电机的短路阻抗由次暂态电抗参数表示；短路后电网上依旧接负荷，近似用恒定阻抗表示，阻抗值由潮流计算结果中的负荷端电压和负荷功率求得。通过戴维南等值方法，在MATLAB中计算交流受端的等值阻抗和解耦系统的各个特征值，解耦后系统等效模型如图5。
算例A和算例B的最大特征值
指标计算值如表1。
应用BPA软件的暂态仿真进行故障模拟，10周波时，直流系统DC2的逆变侧换流母线HLZ22发生三相金属性短路接地，15周波后故障消失。A系统和B系统故障前后受端交流母线电压曲线如图6、图7所示。A系统和B系统故障前后的换流母线频率偏差如图8、图9所示。从图6、图7可看出当故障发生后，受端系统交流母线电压跌落，算例A的HLZ12、HLZ22、HLZ32三条母线电压跌落明显比算例B系统的电压跌落更严重；图8、图9可看出故障后算例B系统比算例A系统母线电压频率偏差更大。所以可以得出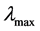
值越小，多馈入系统的静态电压稳定性越好，最大特征值对于多馈入系统的电压稳定有指导意义。
比较最大特征值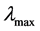
为0.0298的算例A与最大特征值
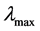为0.0210的算例B仿真结果，对于同样的网络拓扑同一故障条件下，系统B在故障前后交流受端各母线电压波动相比系统A更小，系统B的换
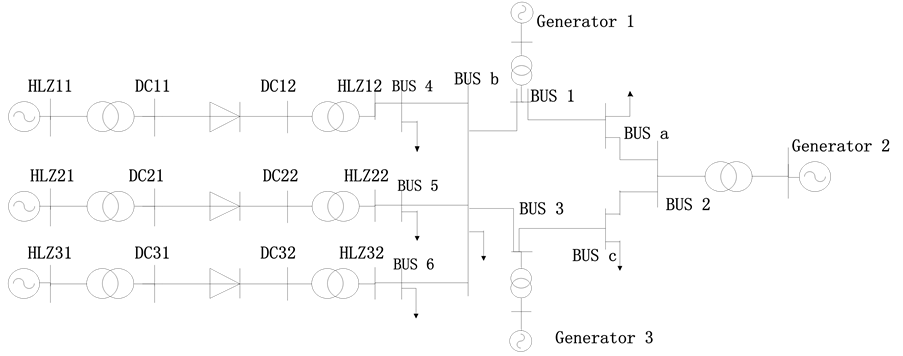
Figure 4. The electrical wiring diagram of the three infeed HVDC system
图4. 三馈入交直流系统电气接线图
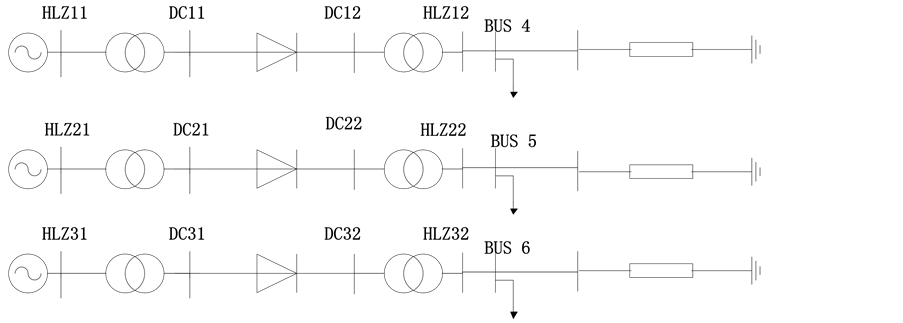
Figure 5. Equivalent circuit of three-infeed example system decoupling model
图5. 三馈入算例系统的解耦模型等值电路
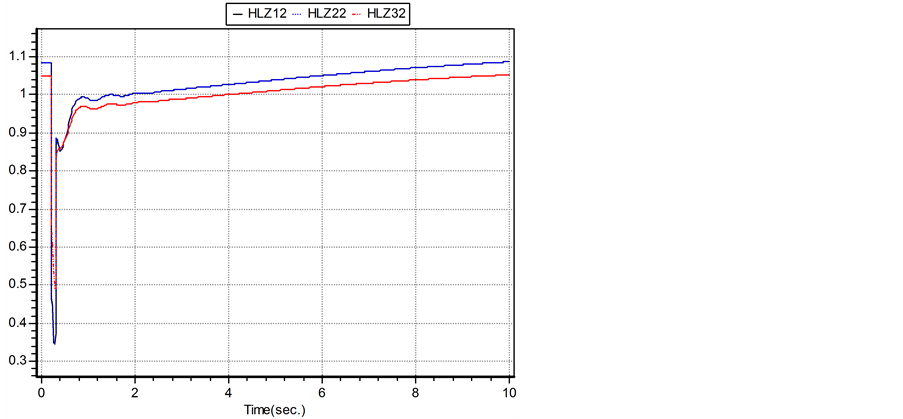
Figure 6. The main bus voltage curve of A system
图6. 算例A交流受端系统母线电压
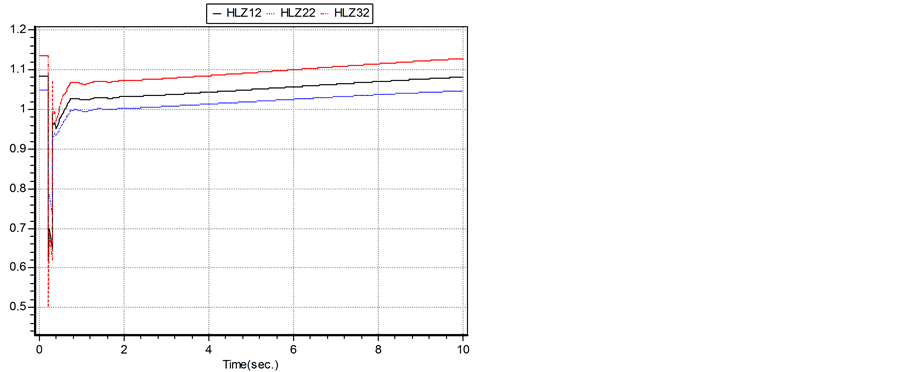
Figure 7. The main bus voltage curve of B system
图7. 算例B交流受端系统母线电压
Figure 8. Frequency deviation of commutation bus of A system
图8. 算例A换流母线频率偏差
Figure 9. Frequency deviation of commutation bus of B system
图9. 算例B换流母线频率偏差
Table 1. Calculation results of maximum eigenvalue
表1. 最大特征值计算结果
流母线频率偏差也比系统A更小，从而说明了最大特征值
越大的多馈入系统交流受端对直流的支撑能力越强，系统电压稳定性越强。
5. 结论
在传统研究多馈入交直流受端系统静态电压稳定的所用的多端口戴维南等值模型的基础上提出了一种多馈入受端系统解耦模型，多馈入交直流系统被等效为多个单馈入系统，实现了多馈入交直流系统的解耦。在解耦模型中，通过分析受端系统等值阻抗矩阵对角化后各个特征值的物理意义，应用单馈入系统静态电压稳定的分析方法提出了新的多馈入电压稳定评价指标(最大特征值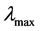
)，并在BPA软件中搭建了两个电气结构相同而新指标
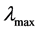计算值不同的简单三馈入交直流系统模型，并进行线路三相短路故障仿真，根据两个系统的电压频率波动图说明了新评价指标对多馈入交直流系统受端电压稳定的分析具有指导意义。
基金项目
国家电网公司科技项目，5201011600TS；国家重点研发计划重点专项，2016YFB0101900。
附录A
Table A1. DC system parameters of example A
表A1. 算例A直流系统参数
Table A2. AC system parameters of example A
表A2. 算例A交流系统参数
Table A3. Impedance and power flow of AC system of example A
表A3. 算例A受端交流系统线路阻抗及潮流
附录B
Table B1. DC system parameters of example B
表B1. 算例B直流系统参数
Table B2. AC system parameters of example B
表B2. 算例B交流系统参数
Table B3. Impedance and power flow of AC system of example B
表B3. 算例B受端交流系统线路阻抗及潮流