1. 引言
自从Wohler在1870年提出材料疲劳寿命和所加交变应力存在一定关系之后,各国科学家一直寻求其最合适的表达式 [1] [2] [3] [4] 。然而,由于疲劳样本容量以及试验机运行时间的限制,常常得不到满意结果。后来美国ASTM提出可由定幅交变应力(应变)下N个疲劳数据先求出平均值及标准差,如果对数平均寿命和对数应力(应变)之间存在线性关系,则可认为各组疲劳命数据服从对数正态分布或者威布尔分布 [1] [3] [4] 。但是由于样本小没能合理验证寿命数据的分布函数,结果不理想。为了改进威布尔寿命数据拟合精度,本作者发展一种新算法,通过调整位置参数和名义最大寿命数据(99%)使得三参数威布尔形状参数κ和疲劳数据内禀斜度/峭度形状参数一致 [5] 。在这个基础上,就可以计算S-N曲线及其标准差和预期寿命L10,L63和L90。
计算方法
威布尔分布
威布尔累计失效率有如下三种形式:
三参数威布尔分布;
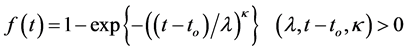 (1-1)
(1-1)
式中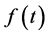 是实测试样在时刻
是实测试样在时刻 的累计失效率。
的累计失效率。 :位置参数,
:位置参数, :形状参数,
:形状参数,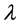 :尺寸参数,是累计失效率达到63.2%需要的时间,它与形状参数
:尺寸参数,是累计失效率达到63.2%需要的时间,它与形状参数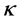 无关。如果
无关。如果 ,它则变成两参数威布尔分布:
,它则变成两参数威布尔分布:
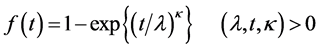 (1-2)
(1-2)
进一步令 以
以 为单位计数,则得到归一化单参数威布尔分布:
为单位计数,则得到归一化单参数威布尔分布:
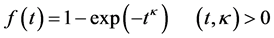 (1-3)
(1-3)
威布尔失效密度分布就是上述诸式对时间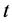 的导函数。威布尔分布参数的各种估算方法已经被详细研究过了 [6] [7] 。现在广为应用的是极大似然法。
的导函数。威布尔分布参数的各种估算方法已经被详细研究过了 [6] [7] 。现在广为应用的是极大似然法。
2. 两参数威布尔分布的拟合
2.1. 极大似然法
设已知一组失效寿命序列(时间或转数) ,分别对应于累计失效率
,分别对应于累计失效率 。对下述极大似然法公式(2)进行迭代计算可获得两参数威布尔分布的最佳参数
。对下述极大似然法公式(2)进行迭代计算可获得两参数威布尔分布的最佳参数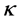 ,然后将所得参数
,然后将所得参数 代入式(3)算出尺寸参数
代入式(3)算出尺寸参数 。为保证结果可靠,本文计算进行到式(2)左边绝对值小于10−5后停止 [7] ,
。为保证结果可靠,本文计算进行到式(2)左边绝对值小于10−5后停止 [7] ,
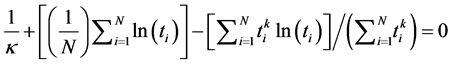 (2)
(2)
 (3)
(3)
由于威布尔分布只在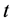 趋近无限大时才等于100%,为了方便,本文设定满足
趋近无限大时才等于100%,为了方便,本文设定满足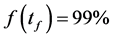 的
的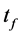 为名义全失效寿命。极大似然法能够保证似然函数极大,但不能保证拟合威布尔曲线和试验寿命的分布形状也一致。因此有必要对试验寿命以及拟合分布曲线的斜度和峭度进行计算和比较。
为名义全失效寿命。极大似然法能够保证似然函数极大,但不能保证拟合威布尔曲线和试验寿命的分布形状也一致。因此有必要对试验寿命以及拟合分布曲线的斜度和峭度进行计算和比较。
2.2. 威布尔分布的斜度和峭度
已知形状参数为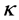 的威布尔分布具有斜度skewness:
的威布尔分布具有斜度skewness:
 (4)
(4)
而过盈峭度excess kurtosis (以下简称峭度)是 [6] :
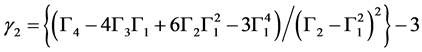 (5)
(5)
式中, ,是gamma函数(i = 1, 2, 3, 4)。统计量
,是gamma函数(i = 1, 2, 3, 4)。统计量 和
和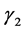 都没有量纲。试样寿命数据的内禀斜度和峭度可由通用统计软件(例如MS OFFICE EXCEL)计算。
都没有量纲。试样寿命数据的内禀斜度和峭度可由通用统计软件(例如MS OFFICE EXCEL)计算。
2.3. 拟合威布尔形状参数κ的具体步骤
为了评价威布尔分布参数拟合的优劣,本文建议采用如下拟合指数 :
:
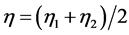 (6)
(6)
式中 ,
,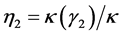 并且
并且 ,
,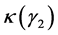 分别是试验数组内禀斜度和峭度的形状参数,
分别是试验数组内禀斜度和峭度的形状参数, 是拟合的威布尔形状参数。显然,当
是拟合的威布尔形状参数。显然,当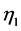 和
和 皆为1或接近1时威布尔形状参数
皆为1或接近1时威布尔形状参数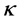 拟合结果最佳。两参数威布尔分布难以达到最佳拟合,这样就需要引入非零位置参数
拟合结果最佳。两参数威布尔分布难以达到最佳拟合,这样就需要引入非零位置参数 (三参数威布尔分布)以及名义全失效寿命
(三参数威布尔分布)以及名义全失效寿命 以提高拟合度 [5] 。
以提高拟合度 [5] 。
具体步骤如下:
1) 先由小到大排列试样疲劳寿命值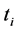 ,用极大似然法算出两参数威布尔分布的形状参数
,用极大似然法算出两参数威布尔分布的形状参数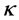 ,与此同时根据试样数组的内禀斜度
,与此同时根据试样数组的内禀斜度 ,峭度
,峭度 计算它们对应的形状参数
计算它们对应的形状参数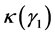 ,
,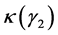 最后得到拟合指数
最后得到拟合指数 。如果
。如果 偏离期望值1较远,则;
偏离期望值1较远,则;
2) 令位置参数 为非零值,调整
为非零值,调整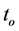 重复步骤1,逐步使
重复步骤1,逐步使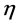 靠近1;
靠近1;
3) 如果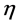 仍然偏离1较远,可调整
仍然偏离1较远,可调整 和名义全失效寿命
和名义全失效寿命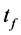 计算
计算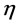 直到它接近最佳值1。这就是拟合的形状参数
直到它接近最佳值1。这就是拟合的形状参数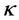 。
。
下面以赵永翔等人的G20CrNi2Mo轴承钢在四种定幅交变应力下(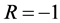 )的疲劳寿命数据 [3] 为例具体说明。
)的疲劳寿命数据 [3] 为例具体说明。
3. G20CrNi2Mo轴承钢的S-N曲线
3.1. G20CrNi2Mo轴承钢疲劳寿命的威布尔分布
赵永翔和梁红琴的疲劳寿命数据见表1。

Table 1. Fatigue life of G20CrNi2Mo steel under four levels of cyclic stress
表1. G20CrNi2Mo轴承钢在四种交变应力下的疲劳寿命,107 cycles
*指经to和tf修正得到最佳拟合指数 后归一化的无量纲寿命:
后归一化的无量纲寿命: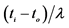 。
。
1) 原始数据的拟合
根据表1四种应力水平的原始数据计算得到的统计量及拟合指数 见表2。显然在前三种应力S1,S2和S3作用下的疲劳寿命数据都得到很好的拟合指数(与最佳拟合指数偏差在5%以内)。但是在最大交变应力S4的场合下,得到的拟合指数
见表2。显然在前三种应力S1,S2和S3作用下的疲劳寿命数据都得到很好的拟合指数(与最佳拟合指数偏差在5%以内)。但是在最大交变应力S4的场合下,得到的拟合指数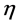 高出最佳值52%。
高出最佳值52%。
 (7)
(7)
式中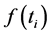 是试验寿命
是试验寿命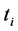 的累计失效率,
的累计失效率,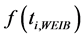 是威布尔分布给出的累计失效率。于是,在四种应力下的威布尔疲劳寿命累积失效率表达式分别是:
是威布尔分布给出的累计失效率。于是,在四种应力下的威布尔疲劳寿命累积失效率表达式分别是:
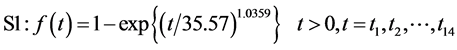
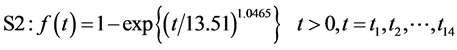
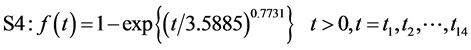
本实验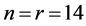 ,
,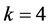 。这四组数据的
。这四组数据的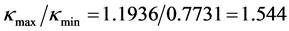 ,可借用McCool提出的判据 [8] :
,可借用McCool提出的判据 [8] :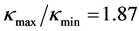 (
( ,
,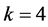 ),可认为四者失效机制相近。
),可认为四者失效机制相近。
2) 数据经过to和tf修正后按斜度和峭度的拟合
四种交变应力作用下疲劳寿命经to和tf修正后的最佳拟合指数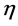 见表3:
见表3:

Table 2. Fitting four original datasets of fatigue life to two parameter Weibull distribution
表2. 四组原始疲劳寿命拟合两参数威布尔分布的结果
符号说明(下同): ,
, :疲劳失效开始时间和名义全失效时间,(107转);
:疲劳失效开始时间和名义全失效时间,(107转); ,
, :极大似然法拟合的威布尔形状参数(无量纲)和尺寸参数(107转);
:极大似然法拟合的威布尔形状参数(无量纲)和尺寸参数(107转);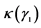 ,
,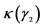 :分别为试样数据内禀斜度和内禀峭度对应的威布尔形状参数;
:分别为试样数据内禀斜度和内禀峭度对应的威布尔形状参数;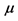 和
和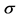 :试样寿命数据的均值和标准差,(107转);
:试样寿命数据的均值和标准差,(107转); :拟合曲线相对于试样实验值的均方偏差(107转)。
:拟合曲线相对于试样实验值的均方偏差(107转)。

Table 3. After correction of and, fitting four datasets of fatigue life to three parameter Weibull distribution
表3. 四组原始疲劳寿命经斜度和峭度修正后拟合三参数威布尔分布的结果
对应三参数威布尔疲劳寿命累积失效率表达式分别是:



虽然Mc Cool提出的判据只适用两参数威布尔分布,这四组三参数威布尔分布的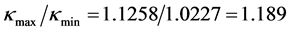 比1.87小多了,应视为失效机制很接近。
比1.87小多了,应视为失效机制很接近。
请注意,经to和tf修正的上述三参数威布尔归一化寿命数据 已列入表1。把这56个数据融合成一组,用极大似然法重新计算拟合指数,得到如下结果,见表4。
已列入表1。把这56个数据融合成一组,用极大似然法重新计算拟合指数,得到如下结果,见表4。
不难看出,融合后数据组的威布尔分布形状参数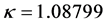 很接近四组
很接近四组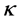 平均值1.09665,尺寸参数
平均值1.09665,尺寸参数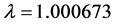 也很令人满意。拟合指数
也很令人满意。拟合指数 也表明归一化数据融合是成功的。
也表明归一化数据融合是成功的。
3.2. S-N曲线
假设对数应力振幅 和对数威布尔尺寸参数
和对数威布尔尺寸参数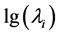 存在线性关系:
存在线性关系:
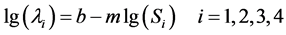 (8)
(8)
式中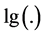 是常用对数,参数b和m可依据最小二乘法解出。
是常用对数,参数b和m可依据最小二乘法解出。
1) 原始数据的S-N曲线
根据表2数据可得到4个应力水平下的常用对数 和
和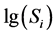 ,并绘成图1。显然,在双对数坐标图上它们存在良好的直线关系。根据最小二乘法,可以得到如下表达式。
,并绘成图1。显然,在双对数坐标图上它们存在良好的直线关系。根据最小二乘法,可以得到如下表达式。

Table 4. After correction of and, fitting normalized four datasets of fatigue life to two parameter Weibull distribution
表4. 疲劳寿命经斜度和峭度修正后归一化融合的两参数威布尔分布

Figure 1. The S-N curve from Weibull distribution of fatigue life data before correction of skewness and kurtosis
图1. 未经斜度和峭度拟合数据的S-N曲线
 (9)
(9)
这与赵永翔等人的结果:指数前因子b = 35.697及斜率−7.592相当接近。
2) 按斜度和峭度拟合的S-N曲线
同理,根据表3数据算出4个应力水平下的常用对数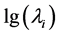 和
和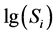 ,可绘制图2。最小二乘法给出这条曲线的表达式是:
,可绘制图2。最小二乘法给出这条曲线的表达式是:
 (10)
(10)
值得注意的是,图2曲线很可能由斜率不同的两线段:1) S1-S3,2) S3-S4组成。大约在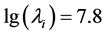 处转折后趋向平缓,进入高周疲劳极限区,但仍未进入无限疲劳寿命区。这种形状的S-N曲线并不少见。如果只拟合线段S1-S3,可得到斜率−4.629319,而线段S3-S4的斜率为−8.387685。由于缺少更多中周和超高周疲劳数据,此S-N曲线是否还有其他转折并不清楚。由于本文只研究S-N曲线的唯象表述,不探讨疲劳失效的微观机理以及超高周疲劳S-N曲线形状分类,对此有兴趣的读者请参考有关文献 [1] [4] [9] [10] 。
处转折后趋向平缓,进入高周疲劳极限区,但仍未进入无限疲劳寿命区。这种形状的S-N曲线并不少见。如果只拟合线段S1-S3,可得到斜率−4.629319,而线段S3-S4的斜率为−8.387685。由于缺少更多中周和超高周疲劳数据,此S-N曲线是否还有其他转折并不清楚。由于本文只研究S-N曲线的唯象表述,不探讨疲劳失效的微观机理以及超高周疲劳S-N曲线形状分类,对此有兴趣的读者请参考有关文献 [1] [4] [9] [10] 。
下面就以经过斜度和峭度拟合的数据组说明S-N曲线的标准差和L10,L63和L90的计算。
3.3. 标准差
若已知形状参数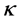 和尺寸参数
和尺寸参数 ,威布尔分布标准差
,威布尔分布标准差 的期望值是:
的期望值是:
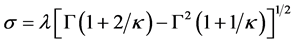 (11)
(11)
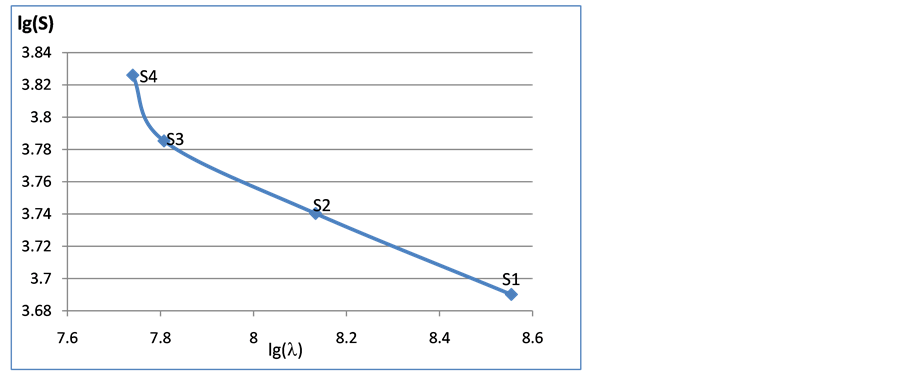
Figure 2. The S-N curve from Weibull distribution of fatigue life data after correction of skewness and kurtosis
图2. 经过斜度和峭度拟合数据的S-N曲线
于是也可以把它和试样数据的内禀标准差进行比较,见表5。显然随应力增大尺寸参数 变小导致标准差减小,这是合理的。此外,实验数据的标准差都略大于威布尔的期望值,也可以接受。
变小导致标准差减小,这是合理的。此外,实验数据的标准差都略大于威布尔的期望值,也可以接受。
3.4. L10,L63和L90的计算
形状参数 在常用范围0.5~5.0内的威布尔累计失效率L10,L63和L90 (10%,63.2%和90%)的数值(以尺寸参数
在常用范围0.5~5.0内的威布尔累计失效率L10,L63和L90 (10%,63.2%和90%)的数值(以尺寸参数 为单位)见图3。当
为单位)见图3。当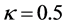 ,L90与L10之间距离超过
,L90与L10之间距离超过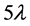 ,但随着
,但随着 值增加,距离逐步减少到
值增加,距离逐步减少到 。因此,只有同时计入
。因此,只有同时计入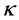 和
和 的影响,计算才可靠。本文
的影响,计算才可靠。本文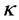 值变化范围不大:1.02~1.22,按此法计算结果见下表6。
值变化范围不大:1.02~1.22,按此法计算结果见下表6。
不难看出,影响L10,L63和L90的主要因素可归咎于尺寸参数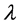 随应力的单调变化。
随应力的单调变化。
4. 结果和讨论
本文用新算法对G20CrNi2Mo轴承钢疲劳寿命的威布尔分布及S-N曲线拟合有如下结论:
1) 通过调整位置参数to以及名义全失效时间tf,G20CrNi2Mo轴承钢在四组定幅交变应力下的疲劳寿命都服从三参数威布尔分布,它们的拟合指数 都很接近1,因此得到的形状参数
都很接近1,因此得到的形状参数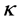 ,尺寸参数和位置参数to都是比较合理的。由于样本寿命在威布尔拟合中采用了三次矩和四次矩,它比现有的拟合方法对样本寿命的随机性要求更严格。不仅保证这两者之间具有最小均方偏差,而且分布密度曲线的不对称性和峰型也比较一致。赵永翔等人的原始数据已经接近要求,只需对to和tf作不大的调整就取得令人满意的拟合指数
,尺寸参数和位置参数to都是比较合理的。由于样本寿命在威布尔拟合中采用了三次矩和四次矩,它比现有的拟合方法对样本寿命的随机性要求更严格。不仅保证这两者之间具有最小均方偏差,而且分布密度曲线的不对称性和峰型也比较一致。赵永翔等人的原始数据已经接近要求,只需对to和tf作不大的调整就取得令人满意的拟合指数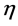 。相信其他研究者只要严格控制试样的制作以及试验参数,也能做到。实际上调整to和tf上只是把寿命数据组内禀的正确统计量
。相信其他研究者只要严格控制试样的制作以及试验参数,也能做到。实际上调整to和tf上只是把寿命数据组内禀的正确统计量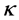 和
和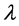 揭示出来。如果经过多次调整to和tf还达不到良好的拟合指数
揭示出来。如果经过多次调整to和tf还达不到良好的拟合指数 ,那可能是样本数量不足,存在系统误差或者疲劳数据服从其他分布所致。
,那可能是样本数量不足,存在系统误差或者疲劳数据服从其他分布所致。
2) 经过调整位置参数to和名义全失效时间tf,四种应力幅值的威布尔寿命形状参数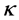 的分散度比未经调整的小得多。可以参考McCool提出的判据。当然
的分散度比未经调整的小得多。可以参考McCool提出的判据。当然 越接近1越好。在各拟合指数
越接近1越好。在各拟合指数 接近1的场合下,用威布尔参数可以得到可靠的S-N曲线,及其标准差和各种累计失效率,供可靠性工程参考。
接近1的场合下,用威布尔参数可以得到可靠的S-N曲线,及其标准差和各种累计失效率,供可靠性工程参考。
3) 本文通过取得在不同应力幅值下寿命数据组的尺寸参数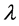 ,能够对应力的影响做出唯象的定量推断。同样也可根据不同环境条件(诸如温度,湿度,酸碱度等等)下尺寸参数
,能够对应力的影响做出唯象的定量推断。同样也可根据不同环境条件(诸如温度,湿度,酸碱度等等)下尺寸参数 的变化,对它们的影响做定量研究。因此本方法有可能在实验数据基础上为工程应用建立S-N曲线数据库。
的变化,对它们的影响做定量研究。因此本方法有可能在实验数据基础上为工程应用建立S-N曲线数据库。

Table 5. The standard deviation of S-N curve from Weibull distribution and that of fatigue data after correction of skewness and kurtosis
表5. 经斜度和峭度拟合的S-N曲线的标准差

Table 6. The L10, L63 and L90 of S-N curve from Weibull distribution after correction of skewness and kurtosis
表6. 经斜度和峭度拟合S-N曲线的L10,L63和L90 in 107 cycles
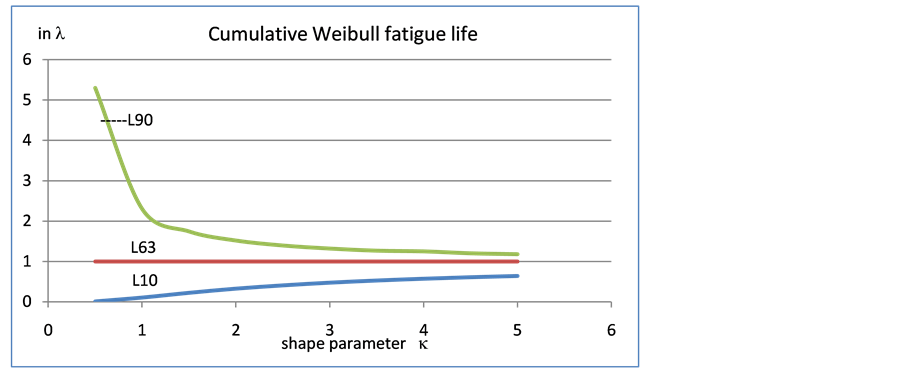
Figure 3. The L10, L63 and L90 of S-N curve from Weibull distribution
图3. 威布尔分布S-N曲线的L10,L63和L90 in λ
4) 本文结论只适用于所述应力区间内极大值与极小值比R为−1的场合。其他场合,例如定幅应变,随机载荷,温度变化,以及腐蚀环境等等须另行研究。至于疲劳裂纹的萌生及扩展的微观机制研究,都不在本文范围,有兴趣的读者可参阅文献 [1] 及 [9] [10] [11] 。