1. 引言
封闭式小区的建设最早开始在80年代初期的美国，后来在我国迅速蔓延 [1] ，但这一居住形式在国外饱受争议。2000年Karina在他的论文中论述了封闭型小区的弊端，主要为与城市交通分离，道路可达性差 [2] 。2003年Susan，Robert和Kent提出通过连接社区的端头路，可以提高城市道路之间的连通性，减少城市交通之间相互冲突的观点 [3] 。2007年Terry，Thorsnes和Appleyard提出通过整合社区和交通用地，来提高出行效率 [4] 。
随着国内机动车数量大幅增加，封闭小区与交通网络的矛盾日益突出，道路交通拥堵问题愈加严重，越来越多的学者意识到开放小区的优越性。邹颖、卞洪斌等(2000) [5] 、曹群英(2001) [6] 和宋伟轩、朱喜钢(2009) [7] 深入分析了我国封闭式小区模式存在的问题；秦葛(2010) [8] 通过建立封闭小区与城市交通发展的协调性评价指标，认为我国封闭小区规划模式已经不能与现阶段城市交通的迅猛发展相协调；徐振宁(2012) [9] 具体说明了现有城市模式使作为“毛细血管”的支路连接较少，一旦干路出现交通拥堵问题，易引起区域性的交通瘫痪。在王受之 [10] 2001年出版的书中鼓励开放混合的居住区新模式，李军(2007) [11] 以实例探讨对比了城市小区的封闭与开放效果，梅策迎(2008) [12] 和周扬(2010) [13] 均提出了通过小区交通开放可以使小区与城市融为一体，增添居住区的活力及有利于构建城市公共交通网络的观点；李向朋(2014) [14] 通过建立城市支路阻抗分析模型——BPR综合模型，利用Braess判断公式对小区交通开放进行了可行性判断，并以对长沙市某小区进行了案例分析。
综合来看，现有国内外研究多为定性分析，定量分析极少且限于对现有封闭小区交通状况的分析，并且将路段和交叉口分开分析，整体性不够，也缺乏小区区位对比。基于以上原因，本文创新性地建立城市饱和度评价模型，将路段和交叉口综合考虑在内，整体评价道路交通状况，模型既适用于城市局部分析，又适用于城市全局分析。同时，通过小区道路开放设计，定量对比了小区开放前后对道路通行的影响，对小区开放缓解交通压力的效果更具说服力。值得一提的是，本文还选择了不同区位的小区以及不同开放程度的小区进行了对比分析，严谨地研究了不同小区对周边道路通行情况影响的差异性。最后，总结研究成果并给出了一般性的结论，就相关部门提出了建设性的意见。
小区周围的道路结构多种多样，本文对于小区周边的研究范围为常见的直接与小区相接的道路以及小区内道路。以地形平坦的城市中最常见的道路网类型–方格网式（又称棋盘式）为例来研究，而目前对交通拥堵的定义尚未统一，实际中拥堵与否大部分还是根据出行者的感受来决定的，因此会因地理位置、出行时间和方式、交通设施类型的不同而不同。为了准确地量化交通拥堵的程度，反映交通拥堵状况，依据完备性、客观性、可操作性、科学性、可比性等原则，将影响因素分为道路设施、交叉口交通状况、路段行驶情况三方面 [15] 。假设小区开放前后道路设施不发生变化，因此，小区周边的道路通行情况主要通过分析路段和交叉路口拥堵情况来评价，其中城市道路交叉口以平面交叉为例。
2. 交通状况评价体系
我们以路段和交叉口通行能力为指标来度量道路疏导车辆的能力，以道路和交叉口的饱和度为指标评价道路的拥堵程度。针对以上两个饱和度指标，以路段和交叉口的面积为权重，我们建立了城市道路交通饱和度函数，以此来评价区域道路整体通行情况。
2.1. 路段通行能力
基本通行能力是指道路和交通处于理想条件下，由技术性能相同的一种标准车，以最小的车头时距(两连续车辆车头端部通过某一断面的时间间隔)连续行驶的理想交通流，在单位时间内(以小时为单位)通过道路断面的最大车辆数。通常，实际道路通行的机动车并非同一类型，但小汽车占多数，因此假设路上行驶的机动车均为性能相同的同一类型小汽车，其长度为实际道路通行车辆的平均长度。路段基本通行能力可表示为 [16] 。
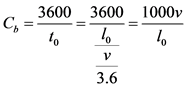(1)
其中
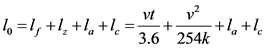(2)
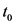为平均车头时距(s)，
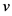为平均行车速度(km/h)，
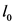为车头最小间隔(m)，
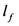为司机在反应时间内车辆行驶的距离(m)，
为车辆的制动距离(m)，
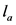为车辆间的安全间距(m)，
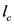为车辆平均长度(m)，
为路面摩擦系数，是与汽车的轮胎花纹、刹车时制动力等有关的量。
受交叉口影响，路段实际通行能力为
，
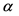为交叉口对路段影响的折减系数。通常情况下，反应时间取1秒 [17] ，安全距离取5米 [18] ，车辆平均长度取5米，则
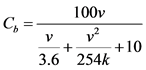(3)
根据《机动车运行安全技术条件》规定的路面摩擦系数，综合考虑小汽车的轮胎花纹与制动能力因素，k取0.78 [19] ，此时可得到不同行驶速度下的路段通行能力，见表1。
Table 1. Basic traffic capacity of the road under different driving speed
表1. 不同行驶速度下的路段基本通行能力
2.2. 交叉口的通行能力
一般来说，交叉口基本有信号等管制，为研究方便，本文中我们假定小区附近的交叉口均有信号灯管制，信号灯是由红、绿、黄三色信号组成。采用国内常用的停车线断面法来计算，交叉口的通行能力为单位时间(以小时为单位)各相交道路进口处通行能力的总和，不失一般性，进口处道路分为右转、左转、直行三种专用通道来考虑，它们各自的通行能力为：
1) 一条专用直行车道通行能力为：
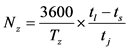(4)
其中，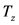
为信号灯周期时间(s)，
前后两车通过停车线的平均间隔时间(s)，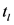
为每个周期内绿灯时间(s)，
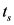为一个周期内的绿灯损失时间(s)，包括启动加速时间。
2) 一条专用右转车道的通行能力为：
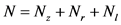
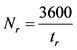(5)
其中，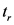
为前后两右转车辆连续驶过停车线断面的间隔时间(s)。
3) 一条专用左转车道的通行能力为：
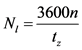(6)
其中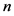
为在一个周期内信号灯周期允许左转的车辆数。
因此，专用车道的交叉口的机动车通行能力为 [20] 。
(7)
根据实际观测数据，在一个以小汽车为主导的路口，信号灯周期时间一般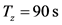
，在这个周期内，绿灯时间
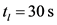，直行车辆通过交叉口的车速，平均为15 km/h；车辆的平均加速度为
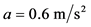，前后车连续通过停车线的平均时间间隔为2.5 s，一个周期内专用于左转车黄绿灯的时间为25 s，左转车辆的平均速度为10 km/h，左转平均加速度为
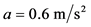，左转车通过停车线的车头时距为2.5 s。通过计算可得到交叉口总的通行能力为
。
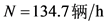2.3. 交叉口对路段通行能力的影响
交叉口在城市交通通行能力中具有重要的作用，特别是在交叉口之间的间距较小时，对通行能力有很大的影响。小区开放后，增加了交叉路口，因此部分交叉路口之间的距离也会变化，由此影响到了特定路段的通行能力，因此，有必要引入交叉口通行能力折减系数来表示其对路段通行能力的影响。
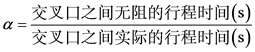(8)
无阻时的行程时间可以通过交叉口之间的距离除以路段上的行车速度来算，实际行程时间可以引入启动时加速度与刹车制动时的加速度，在无阻时的行程时间上进行调整得到。可用如下表达式：
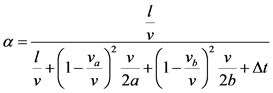(9)
其中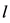
为交叉口之间的距离(m)，
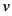为路段上的行车速度(m/s)，
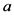为汽车起动时的平均加速度(m/s2)，
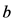为汽车刹车制动时的平均加速度(m/s2)，
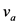为加速车辆到达交叉口的车速(m/s)，
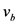为减速车辆到达交叉口的车速(m/s)，
为车辆到达交叉口后在此的等候时间(s) [20] 。
2.4. 城市道路交通饱和度
道路交通饱和度是用来衡量道路的拥堵程度，若道路的通行能力为C，道路的实际车流量为V，则道
路饱和度可表示为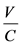
。于是，若路段的通行能力为
，实际车流量为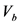
，则路段的饱和度为
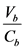；假定研究的道路有
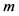个交叉口，若第
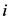个交叉口的通行能力为
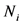，实际车流量为
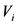，则第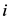
个交叉口的饱和度为
。
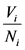在现实中，城市的交通饱和度是由路段饱和度和交叉口饱和度共同决定的，因此，我们将以上两个因素综合考虑在内定义城市道路交通饱和度函数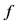
。以路段面积和交叉口面积为权重分别对路段饱和度和交叉口饱和度进行赋权，得到城市道路交通饱和度函数
：
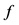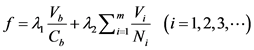(10)
其中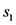
为路段的面积，
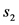为交叉路口的面积，两个指标的权重分别为
，
。
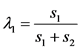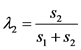我国一般根据饱和度值将道路拥挤程度、服务水平分为四级 [21] ，见表2。
3. 实证分析
我们以常见的三类小区为例，通过计算城市道路交通饱和度函数，来讨论开放前后对交通通行能力的影响。
3.1. 市区双开口开放小区
市区小区周边道路多为图1所示。
根据《中华人民共和国道路交通安全法实施条例》(以下简称《条例》)，市区内小区周边路车速取为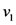
为40 km/h。小区开放后，其内部道路车速取为
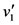为20 km/h [22] 。经过连续一周的高峰时间段实地数据调查，此小区及周边道路构成的系统内高峰期一小时车流量平均为4537辆。模型求解如下：
1) 权重计算
开放前：路段所占权重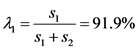
，交叉口所占权重
。
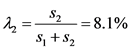开放后：路段所占权重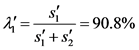
，交叉口所占权重
。
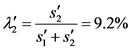2) 折减系数计算
通过计算得到不同情况下的折减系数。由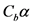
，计算出各路段的实际通行能力，小区的相关数据见表3，其中路长和路宽均来自实际测量数据。
表2. 道路服务水平
Table 3. The related data sheet of urban area 1
表3. 市区小区1相关数据表
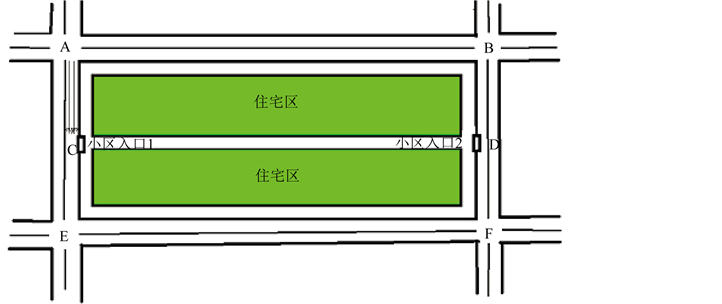
Figure 1. Simplified figure of urban area 1
图1. 市区小区1简化图
3) 把相关数据代入(10)式得到开放前后城市道路交通饱和度函数值。
开放前：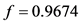
，开放后：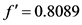
。
4) 结果分析
，开放前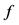
为三级偏下服务水平，小区开放
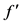接近二级服务水平。
同样的车流量，开放小区后其周边的交通接近二级服务水平，整体来看开放小区有利于优化路网结构，缓解交通压力。但通过表中纵向道路实际通行能力的数据可以发现，小区开放后所直接连接的实际道路通行能力有所下降。这表明小区的开放对所连接道路的通行能力具有一定的影响，但从整个系统中看，小区的开放对交通状况的改善具有积极作用。
3.2. 郊区双开口开放小区
城市郊区小区周边道路常为图2所示：
根据《条例》，郊区的小区周边路平均车速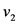
为60 km/h。小区开放后，其内部道路车速平均
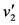为20 km/h [22] 。经过连续一周的高峰时间段实地数据调查，此小区及周边道路构成的系统内高峰期一小时车流量平均为2408辆。模型求解如下：
1) 此求解过程似3.1，得到相关数据如表4所示。
其中路长和路宽均来自实际测量数据。
2) 城市道路交通饱和度函数的计算：
开放前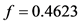
，开放后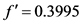
。
3) 结果分析：
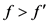，小区开放前后均为一级服务水平。
同样的车流量，小区开放前道路服务水平处于一级服务水平，小区开放后，虽然道路饱和度函数值有所下降，但变化不大，道路服务水平依然处于一级。由此看出，对于交通压力不大的小区及周边道路，小区的开放没有太大的影响。
3.3. 市区小区四开口开放小区
市区另一常见小区如图3所示。
根据《条例》，市区内小区周边路平均车速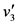
为40 km/h。小区开放后，其内部道路车速平均
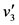为20 km/h [22] 。经过连续一周的高峰时间段实地数据调查，此小区及周边道路构成的系统内高峰期一小时车流量平均为4537辆。模型求解如下：
1) 此求解过程似3.1，得到相关数据如表5所示。
其中路长和路宽均来自实际测量数据。
2) 城市道路交通饱和度函数的计算开放前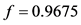
，开放后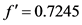
。
3) 结果分析：
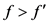，小区开放前为三级服务水平，开放后为二级服务水平。
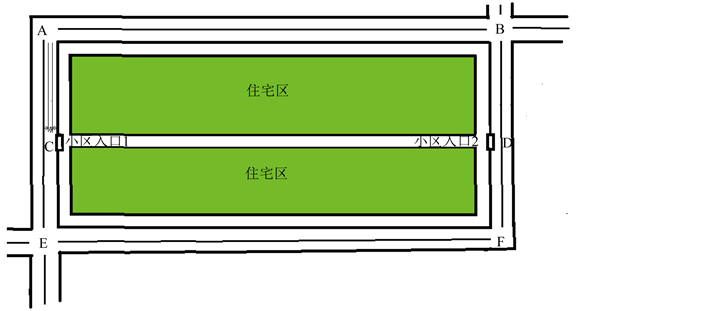
Figure 2. Simplified figure of suburban area 2
图2. 郊区小区2简化图
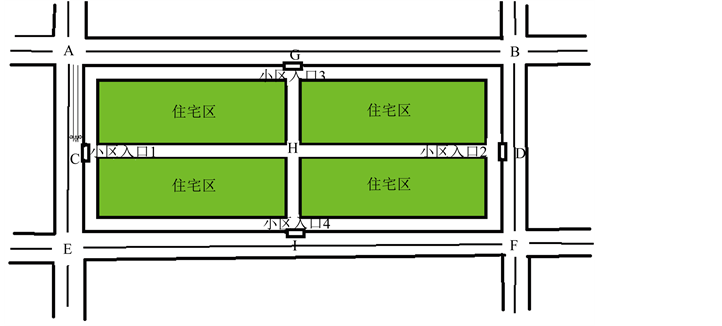
Figure 3. Simplified figure of urban area 3
图3. 市区小区3简化图
Table 4. The related data sheet of suburban area 2
表4. 郊区小区2相关数据表
Table 5. The related data sheet of urban area 3
表5. 市区小区3相关数据表
由上表横向和纵向的实际通行能力数据可以看到，由于增加了小区道路使得各条主路的通行能力均有所下降，但是因为小区道路的分流作用使得整体的道路饱和度有很大的降低。此小区的道路服务水平由三级偏下，大幅提高到了二级中等水平，因此，可以认为在此模型下，对于小区及周边道路系统的交通压力缓解具有显著作用。
4. 结论与评价
4.1. 结论
1) 对于市区的两个小区，开放两条道路后周围道路整体效果明显优于开放一条道路。但是通过具体路段开放前后的通行能力对比可以看出，开放后与小区直接相接路段的通行能力也下降，因此小区道路开放并不是开口数量越多越好，而应该考虑到小区及周边的情况具体分析。
2) 对比市区与郊区的双开口开放小区，由于郊区的车流量并不大，所以开放对于整体的交通状况并没有太大的提升，反而使得部分路段的通行能力有所下降。因此对于小区及周边道路系统交通状况本身就良好的小区，小区的开放没有太大意义。
4.2. 评价
1) 本研究将模型假设为所有道路交叉口均有信号灯，但实际中有较多小区开放后，其道路与周边道路的交叉口没有信号灯控制，因此模型未来的改进可以将无信号灯交叉口的通行能力考虑在内，来更加精准地结合实际情况对道路通行能力进行评价。
2) 本研究在模型假设中，以同一类型的小汽车为例进行了研究，尽管以实际道路通行车辆的平均长度作为小汽车的长度，但并没有考虑到货车、客车、公交车等不同性能的机动车辆对模型的影响。在实际分析中，可以根据研究的具体道路中通行的实际车辆类型，对模型进行优化。
5. 启示与建议
1) 关于小区开放的建议：小区及周边道路系统的交通压力很大时，小区的开放对于优化路网结构，缓解交通压力具有一定作用，但是对于类似于郊区等开放前交通压力就较小的区域，效果不大，反而会造成所连接的路段通行能力的降低，因此小区的开放对于繁华地区即交通压力较大的地区很有必要，但对于交通压力不大的区域没有必要。
2) 对于小区开放道路数量的建议：在一定范围下，开放更多的道路，对于交通压力的缓解作用更明显，但开放更多的道路会造成具体路段的通行能力下降，当增加到一定数量后，就会导致小区及周边道路系统的交通能力的下降，反而不利于交通压力的缓解；而且开放道路也会引起小区内的安全保障、道路的维护等问题。因此对于小区的开放道路数量需要对小区规模、开放前小区周边交通压力大小、物业管理等因素进行综合考虑后确定。
基金项目
北京高等学校“青年英才计划”(YETP0769)，国家自然科学基金(61571002, 61370193)，中央高校基本科研业务费专项资金资助(项目编号：2015ZCQ-LY-01)。