1. 研究背景
粮食是人类生存最基本的生活消费品，一个国家的粮食问题是关系到本国的国计民生的头等大事 [1] 。建国以来我国的粮食产量多次出现了波动，这不仅制约了国民经济的发展，而且给粮食生产者和消费者都带来了极为不利的影响。粮食生产关系到我国的社会经济发展，因此认真研究和加深了解中国粮食生产的主要因素，并采取针对性的粮食增产措施。对于稳定和发展粮食生产具有重要意义。
在我国，粮食生产具有特别重要的意义。我国是世界人口第一大国，来自人口的压力直接作用到粮食生产上。因此，对我国粮食生产的影响因素进行定量分析，研究粮食产量涨落的原因以及提供某些政策建议是十分必要的。改革开放以来，我国粮食产量从总趋势来看是增长的，然而对总趋势作进一步分析发现，以曾创历史最高纪录的1984年为界，向前推到1978年，这段时期，增长势头较猛，增长率较高，1984年到今这段时期，粮食产量的总趋势是增长的，但这增长是在波动中的增长，这其中的原因可以从粮食产量的影响因素中得到解释。
我们知道，在1978~1984年的粮食市场，实行的是政府定价的统购统销政策。1985年以后逐步放开粮食市场，中间有过几次政策的反复，直到2004年才实现购销的市场化。根据我们收集的资料表明：在1985~2006年的22年时间里，我国经历了三次比较明显的粮食涨价(粮食生产和零售价格同比增长 > 10%)，他们分别是1988~1989，1992~1995和2004。而从1979~1999年间的粮食产量和实际收购价格波动(已扣除了通货膨胀因素)情况看。这21年间有5年增产幅度接近10%，有6年比上年减产，个别年份减产幅度达7%。但粮食生产波动的方向在大多数年份与粮食价格的波动相吻合。1993年底至1996年，粮价经历了3年的上涨，1997年至2003年又经历了近7年的下跌和持续低迷。从1995年开始，我国连续4年粮食丰收，再加上1995年至1998年粮食净进口2500万吨，导致粮食年总供给量大于消费量，出现了结构性过剩。1999年以来，我国粮食产量持续下降和徘徊，进入一个新的变动周期。粮食连续4年减产。1999~2003年，全国粮食最大减产幅度达7774万吨。客观讲，减产趋势是对上一轮超常增产周期的合理回归。
本文选取1978年至2016年粮食产量作为样本数据 [2] ，用干预模型对粮食产量进行分析，判断出从1978年至2016年期间粮食产量波动较为明显的时间，找出合适的干预模型进行预测并给出合理的建议。
2. 干预分析模型的简介
时间序列经常会受到特殊事件及态势的影响，诸如国内经济政策或经济规则的变更、国际政治局势的骤变，以及节假日、罢工、贱卖、促销之类事件的影响等，学者们称这类事件为干预事件。陈兆友利用福建省1979~2008年的FDI数据，运用干预模型和Chou突变点进行分析，最后得出FDI对福建省第三产业结构存在干预作用 [3] 。王鑫等人将干预模型与BP神经网络相结合，利用1978~2004年的数据建立预测模型，得出了2005~2009年的GDP数据 [4] 。
研究干预分析的目的，就是从定量分析的角度来评估政策干预或突发事件对经济环境和经济过程的具体影响。一般来讲，干预分析模型是与事件序列模型结合起来进行研究的。经济政策的变化或突发事件的影响不能忽视，在干预事件发生后，序列是否存在事实上的变化？若有影响，其影响程度又如何？这就是干预分析模型所要解决的问题。
干预分析模型是传递函数模型的一种推广，当不存在干预影响时，这两种模型没有本质上的区别。由传递函数发展到干预分析的过程，类似于从多元回归分析发展到虚拟变量的应用。干预分析与回归分析中虚拟变量之间的主要差别是：前者为动态模型，后者为静态模式；前者是一个过程，后者是单个或多个变量。因此，干预分析模型的研究，无论从内容上还是方法上，都要比虚拟变量复杂得多。
2.1. 干预变量的形式
干预分析模型的基本变量是干预变量，有两种常见的干预变量：一种是持续性的干预变量，另一种是短暂性的干预变量。在这里，我们主要分析的是持续性的干预变量。表示
时刻发生以后，一直有影响，这时我们可以用阶跃预函数，形式是：
(2.1.1)
2.2. 干预事件的形式
干预事件虽然多种多样，但按其影响的形式，归纳起来基本上有以下四种类型 [5] ：
1) 干预事件的影响突然开始，长期持续下去
设干预对因变量的影响是固定的，从某一时刻
开始，但影响的程度是未知的，即因变量的大小是未知的。这种影响的干预分析模型为：
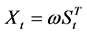(2.2.1)
在这里，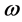
表示干预影响强度的未知参数。有时候
不一定是平稳的，要求通过差分化为平稳序列，则干预分析模型可调整为：
(2.2.2)
其中，
为后移算子。
如果干预事件要滞后若干个时期才产生影响，如
个时期，那么，干预分
型模型可进一步调整为：
(2.2.3)
2) 干预事件的影响逐渐开始，长期持续下去
有时候干预事件突然发生，并不能立刻产生完全的影响，而是随着时间的推移，逐渐感到这种影响的存在。这种形式的一般模型为：
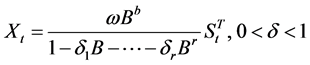(2.2.4)
3) 干预事件突然开始，产生暂时的影响
这类干预事件可以用数学模型描述如下：
(2.2.5)
当
时，干预的影响只存在一个时期；当
时，干预的影响将长期存在。
4) 干预事件逐渐开始，产生暂时的影响
干预的影响逐渐增加，在某个时刻达到高峰，然后又逐渐减弱直至消失。这类干预事件可以用一下模型描绘：
(2.2.6)
不论经济系统如何受到多种干预的影响，也不管这些影响是多么复杂，归纳起来，都可以用以上四种形式或者他们的某种组合来表示。同时，也可以用这种组合去模拟多个干预事件所产生的影响。
从干预分析模型的形式可以看出，当选择恰当的干预变量后，干预模型可以较好地反映变量波动的情况，特别是在有大级别的干预事件发生时，如房地产中的价格指数中的“政策干预”与“庄家干预”事件等。因为一般的时间序列模型，如ARIMA模型、ARCH模型，是难以对这样具有“突变性”的时间序列进行模型化处理的，而干预分析模型将干预因素体现在了干预变量中，恰恰可以较好地解决这一问题。
2.3. 干预分析模型的识别与参数估计
干预分析模型的主要目的是为了测度干预效应，就干预变量而言，剔除了干预影响后的序列，可看作普通的时间序列，今儿可以用一般的时间序列分析方法进行拟合，如博克斯-詹金斯法，以及多项曲线、指数曲线、生长曲线等非线性方法。这里以博克斯-詹金斯法的ARIMA模型为例进行说明。
设平稳化后的单变量序列满足下述模型：
(2.3.1)
又设干预事件的影响为
，这里
为干预变量，它等于
或
，则单变量序列的干预分析模型为：
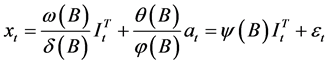(2.3.2)
这里：
，
(2.3.3)
在此模型基础上，要根据序列变化的现实资料，对
与
进行识别。
3. 全国粮食产量干预模型分析
3.1. 问题的提出
根据大量资料及已有的研究成果，我们发现中国粮食产量波动具有一定的周期性并且粮食产量的增长与波动总是相对应地交替形成和出现。从新中国成立以来的粮食波动看，每当粮食生产连续增长几年后，总是由于外界因素的影响，粮食增长率降到一个相对较低水平，并在这个水平上持续几年的徘徊。这种周期性，体现了粮食生产波动形成的规律性特征。如20世纪70年代末以来，中国“卖粮难”、“买粮难”现象反复交替出现，粮食市场价格波动十分显著，粮食市场陷入一种“短缺”与“过剩”交替发生的循环波动之中，粮食政策陷入了“多了放、放了少、少了统”的怪圈。年度连续性是中国粮食产量波动的另外一个特点，这体现了粮食产量一旦下降就需要很长时间才能恢复过来的特点。尤其是近十年来体现尤其明显。1998年粮食产量达到一个高峰51,229.5万吨后，就出现四年减产周期，而且从2004年到2008年这连续五年增产后才恢复到原来的水平。
从2000年到2003年，中国的粮食产量已将连续四年下降，2003年中国的粮食产量只有4.35亿吨，降到警戒线4.85亿吨以下几千吨。造成这几年粮食下降严重的原因是因为农民没有的种粮的积极性，因此即使有好的技术仍然无法提高我国的粮食产量。
同时，2003年我国的粮食播种面积已经不足15亿亩，是建国以来最低的粮食播种面积。从1997年到2002年，我国的耕地面积净减少了6164万亩，平均每年减少1200多万亩。最近几年因为各方面的开发用地，我们的耕地已经损失了6000多万亩。由于很多地方在进行地区开发，有许多大工程，导致许多好的田地被占用。还有国内的污染现象越来越严重，如土地沙漠化等；许多地区在当时都提高了经济作物和优质农产品的种植，而当时的高层对粮食问题的乐观估计在一定程度上动摇了中国长期坚持的“以粮为纲”的观念。城市发展大量占用耕地面积，以及某些地方盲目推行“退耕还林、退耕还草”政策，导致全国粮食播种面积锐减。
已知政策对粮食产值的影响是逐渐开始的，又是逐渐达到高潮的，环境因素对粮食产量的影响也是逐渐开始的，会产生持续的影响，在2004年我国的粮食产量又开始增长。
本文选取了从1978年~2016年我国的粮食产量数据，按照粮食产量的变化趋势将粮食产量变化的发生分为两个时期：第一个时期为1978年到2002年，共有25个数据；第二个时期为2003年到2016年，共有14个数据。由于这些因素的发生并不是立刻产生完全的影响，而是随着时间的推移，逐渐地感到这种影响的存在，因此，干预模型应选取以下模式：
(3.1.1)
其中：
(3.1.2)
按照单变量时间序列模型的干预分析进行建模计算。原始数据如下表1所示。
3.2. 干预分析模型的识别与参数估计
1) 根据1978年到2002年，即前25个历史数据，建立时间序列模型(表2)。
这里经过观察与筛选，最终选取三次曲线模型进行拟合，结果如下：
(3.2.1)
其中
，
(
高度显著)，说明模型拟合效果很好。
2) 分离出干预影响的具体数据，求估干预模型的参数
运用经过检验的三次曲线模型，进行外推预测2003年到2016年的粮食产量预测值
，然后用实际值
减去预测值
，得到的差值就是政策产生的效益值，记为
，具体数据如表3。
运用上表的数据，可以估计出干预模型
表1. 原始数据序列
Table 2. Model summary and parameter estimates
表2. 模型汇总和参数估计值
表3. 干预影响序列
(3.2.2)
中的参数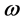
与
，实际上是自回归方程
的参数：
从表4我们可以得出干预模型的参数是
(3.2.3)
其中
(高度显著)，模型系数的
检验也是高度显著的，说明模型拟合效果很好。
3) 计算净化序列
净化序列是指消除了干预影响的序列，它由实际的观察序列值
减去干预影响值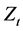
得到，即：
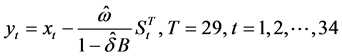(3.2.4)
在这里，
称为消去了干预影响的净化序列，具体计算数据如表5。
4) 对净化序列建立拟合模型
如表6，仍选取三次曲线模型进行拟合，结果如下：
(3.2.5)
其中，其中
(高度显著)，说明模型拟合效果很好。
5) 组建干预分析模型
表4. 系数表
Table 5. Sequence of eliminating effects
表5. 净化序列
结合
的拟合模型(3.2.5)式与干预参数
、
的估计值(3.2.3)式，代入(3.2.4)式，得到所求得干预分析模型：
(3.2.6)
其中：
利用干预模型分析预测模型计算出预测值
，并与原始值
比较，我们可以得出如图1。
从图中，可以看出两个序列重合度较高，说明干预模型在这里取得了不错的效果。因此我们可以对数据进行预测，以下是未来两年我国粮食产量预测值(表7)。
4. 结论及建议
干预模型中参数
是截距，表示各因素对粮食产量增加值的初始影响程度；参数
为斜率，用来表
Table 6. Model summary and parameter estimates
表6. 模型汇总和参数估计
表7. 预测值
Figure 1. Forecast on intervention model
图1. 干预模型预测效果图
示这种影响的趋势。通过建立干预模型来对我国粮食产量进行预测，可以发现预测的效果还是挺好的，误差在允许范围之内，因此我们认为干预模型在短期的粮食产量预测中得出的结果是比较准确的。通过对实际值和预测值进行精度计算，选取
，则发现相对误差
。相对误差小于5%，因此认为此干预模型拟合效果较好，可以用来对数据进行比较准确的预测。
虽然未来几年粮食产量呈递增趋势，但是国土资源部日前公布的调查数字显示，我国人均耕地面积由2004年的141亩进一步减少到2005年的114亩，城市化、工业化不得不再占用耕地、国家实施生态退耕工程也要减少耕地。从141到114，反映出我国耕地面积持续减少的趋势尚未发生根本改变。并且近年来城市化和工业化不得不再占用耕地，在耕地不足的情况下，为减少污染而将减少化肥施用量，粮食产量还有可能产生波动，粮食增产会更多地依赖于技术的进步。所以提出以下保持增产的建议：
1) 稳定粮食播种面积
一方面是坚持最严格的耕地保护制度，控制非农业占地，建立基本农田保护区，确保基本农田总量不减少、质量不下降。一方面是加强对现有耕地的开发，通过进一步改进耕作制度和应用优良品种，保持相对稳定的粮食作物播种面积，提高耕地利用效率 [6] 。
2) 提高农民素质 [7] ，增加农业的人力资本投入
从当前和将来的农业发展趋势来看，农村劳动力向城市大量转移不可逆转，传统的劳动密集型农业模式难以维持，只有向资本、技术密集型农业转变，提高单个农民的生产率，才能保持粮食生产不断递增的趋势。
3) 推行农业标准化，发展节约型农业
科学施用化肥、农药和农膜，推广测土配方施肥、平衡施肥、缓释氮肥、生物防治病虫害等实用技术，建立农田生态系统的良性循环。大力推广作物高效节水技术，提高水分和肥料利用效率。推广先进适用农机具，提高农业机械化水平。