1. 引言
电力对国家的安全、社会的稳定发展以及人民生活有着重大的影响。电能的主要特点就是不能存储,要求随发随用,因此,电能的产生过程要求较高,既不能发电多于用户所需,也不能发电少于用户所需。电力负荷预测即要求能通过对历史负荷数据的全面分析,根据所得到的预测的负荷数据,可以用来提前安排发电计划,提高电网的可靠性和安全性。随着社会的发展,电力负荷的预测方法也越来越多,从最初的手工计算,到如今众多学者提出了越来越多的方法,负荷的预测精度也越来越高。电力系统负荷的预测,一方面与负荷本身的历史规律有关,如节假日,季节,地区的影响,同时,还受到气象、经济等因素的影响 [1] - [7] 。科学的负荷预测可以作为电力系统的规划,调度等部门工作的依据,能保证电力系统做出正确的决策。现有的预测方法主要有:传统的经验式计算法、回归分析法、专家系统法、时间序列法、小波分析法、模糊预测法和人工神经网络等 [6] [7] [8] [9] 。由于短期负荷的周期性和气象规律性,可以根据历史负荷数据,通过网络训练,达到自学习能力。负荷预测是一个典型的多(单)输入,单(多)输出的非线性系统,与人工神经网络模型非常接近。因此,众多预测方法中,人工神经网络得到了最为广泛的应用。但单一的神经网络在负荷预测中的缺点就是收敛慢,容易陷入局部极小值等。近年来,随着科学计算技术的不断发展,启发式算法也受到了学者的普遍关注,许多学者也提出了一系列的方法对神经网络进行改进,如遗传算法,粒子群算法等 [2] [7] [10] 。通过研读文献,发现海豚算法(DPO)较遗传算法(GA)、粒子群算法(PSO)等早先提出的算法具有收敛速度快、易跳出局部最优解的优点 [10] ,本文就海豚群觅食行为提出一些自己的改进方法,使用海豚算法对BP网络进行优化,并与粒子群算法优化BP网络进行对比,结合短期负荷预测证明多维情况下海豚算法优化BP神经网络(DPO-BP)的优越性。
2. BP神经网络在负荷预测中的应用
2.1. BP神经网络输入输出变量的选择
设待预测的日期为DAY,要预测的数据为该天1~24小时的整点负荷值。可以通过两种方法构建预测模型:1) 构建多输入,24个输出的网络,对预测日的24小时负荷进行预测;2) 构建多输入,单输出的网络,对预测日指定时刻t的负荷分别进行预测,但是,要预测一天24小时的负荷,就要分别构建24个这样的网络。考虑到第一种方案输出变量过多,相应输入变量要比第一种方案多很多,网络结构太大,为了减少网络计算量,本文采用后一种预测方案。
因此,样本的输出变量为预测日t时刻的负荷,取时间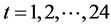 。已知所有样本的负荷数据(即每天每个小时的负荷数据)和每天的平均气温。选取影响负荷预测的因素有气温、前一天的多点负荷数据、前两天的多点负荷数据,前三天的多点负荷数据等16种。在此,样本的输入变量
。已知所有样本的负荷数据(即每天每个小时的负荷数据)和每天的平均气温。选取影响负荷预测的因素有气温、前一天的多点负荷数据、前两天的多点负荷数据,前三天的多点负荷数据等16种。在此,样本的输入变量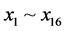 ,输出变量y的具体含义如下表1所示。
,输出变量y的具体含义如下表1所示。
2.2. 数据预处理
采用欧洲某地区的样本数据,该数据来源于http://neuron.tuke.sk/competition/index.php,对该地区指定日期的电力负荷进行24小时预测。预测之前先要对历史负荷数据进行数据预处理,以去掉影响负荷预测的伪数据。首先,相邻日相同时刻的历史负荷具有相似性,若某一天某一时刻的负荷数据波动超过了前后七天同一时刻的一定范围,就可以认为是伪数据,根据所设定的最大波动范围,取设定的最大值或最小值。同时,在每一天的负荷历史数据中,前后两时刻的负荷不应出现特别大的波动,设定前后两时刻负荷数据为基准值,设定数据的最大的横向波动范围,若某点负荷数据与前一时刻的数据和后一时刻的数据差都超过阀值,就认为该点是伪数据,可以用前一天三个时刻的数据和当天的前后数据对当天时刻的负荷数据进行修正。
样本数量从
1998 年 7 月 6 日
到
8 月 6 日
共选取为32组。通过前面多组数据预测
8 月 6 日
的指定时刻t的负荷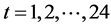 。由于样本数据某些影响因子之间相差的数量级较大,需要对样本进行无量纲化处理。选取式(1)作为归一化函数,将每个数据都归一化到
。由于样本数据某些影响因子之间相差的数量级较大,需要对样本进行无量纲化处理。选取式(1)作为归一化函数,将每个数据都归一化到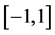 内:
内:
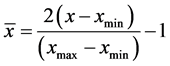 式(1)
式(1)
其中: 为处理之前的值,
为处理之前的值,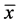 为处理之后的值。
为处理之后的值。
2.3. BP神经网络对电力短期负荷预测算法的实现
BP网络是一种多层次的前馈结构型神经网络。BP神经网络主要的特点是信号的前向传播,误差的反向传递。在前向传播过程中,输入信号起始于输入层经隐含层逐层向后传播,最后终止于输出层。每一层神经元状态只影响其下一层的神经元状态。如果输出层得不到期望的输出,则开始进行反向传播,依据预测误差值来调整网络权值或阈值,从而使BP神经网络预测结果不断地逼近期望输出。本文使用的BP神经网络的层次结构如图1所示。
图1中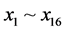 表示BP神经网络的输入值,
表示BP神经网络的输入值,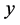 表示BP神经网络的输出预测值,
表示BP神经网络的输出预测值,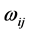 和
和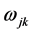 为BP神经网络的权值。从图1中可以看出,BP神经网络可以视为一个非线性函数,网络的输入值和输出值分别视为该非线性函数的自变量和因变量。依前所述,本文设置网络侧输入层的节点数为16,输出层的节点
为BP神经网络的权值。从图1中可以看出,BP神经网络可以视为一个非线性函数,网络的输入值和输出值分别视为该非线性函数的自变量和因变量。依前所述,本文设置网络侧输入层的节点数为16,输出层的节点

Table 1. Input variables and output variables
表1. 输入变量和输出变量
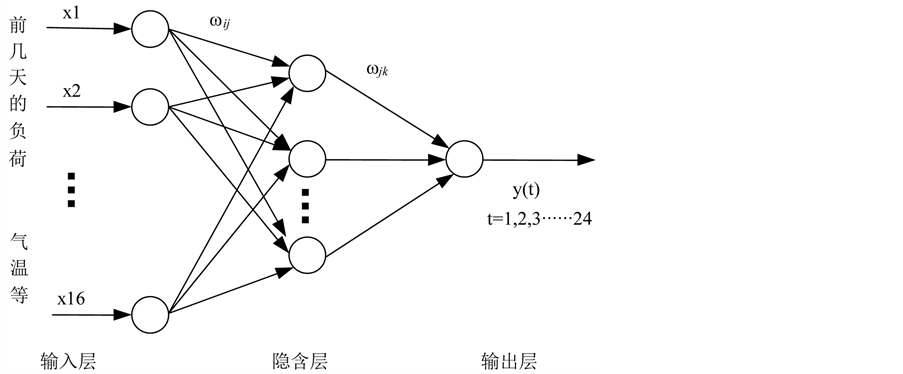
Figure 1. The topology of the BP neural network
图1. 本文使用的BP神经网络的拓扑结构
数为1,该BP神经网络可视作从16个自变量到1个因变量的非线性函数的映射关系。隐含层通过试凑法确定为11个。同时,将样本分为训练样本和测试样本,测试样本为1组,即
8 月 6 日
的24小时负荷值分别作为每个网络的测试样本。网络实际训练时,发现当训练样本个数太多时,24小时的最大预测误差较大,当训练样本增加到30个时,24小时的最大预测误差达到了8.4%。原因应该是电力短期负荷自身特点导致,由于电力负荷的短期预测直接受近期负荷影响,当训练样本过多时,容易使网络训练过度,网络记住了个别特征如较远时期以前样本的影响从而导致预测误差增加 [11] 。通过反复训练,最终确定采用10个训练样本,1个测试样本,BP神经网络预测效果较好,但是24小时的预测误差最大值也达到5.7%,网络的训练效果受其初始权值、阈值的影响较大,预测效果并不理想。因此,需要对算法进行改进,提高负荷的预测精度。
3. 海豚算法(DPO)优化BP神经网络
3.1. 基本思想
DPO算法采用海豚觅食过程中从个体到种群的设计方案和分工明确的互助式探索路径的结构。如图2所示,通过海豚个体对自身位置和食物位置的感知和判断、群体间的信息共享,自主进行个体的角色定位,选择首领,以期获得靠近食物的最优位置 [10] [12] 。文献10通过测试函数测试了DPO的搜索性能,DPO比GA算法更易跳出局部极值点,相比标准PSO算法,收敛速度更快。
3.2. DPO-BP算法基本思路
传统BP神经网络这个单一的算法,各网络层的阈值以及各层网络间的连接权值都是随机生成的,虽然BP网络自身也有对网络的连接权值、阈值进行更新,但是这种更新的效果并不理想 [10] 。因此,BP网络预测的准确性受到初始权值、阈值影响很大。基于此,一些学者阐述,只要多运行几次总会得到一次较好的训练、测试结果。显然,这种方法并不是根本的解决之道。
启发式DPO算法,在总结海豚觅食行为的基础上,通过位置初始化、适应度(目标)函数值计算、群体交流、位置更新等步骤,逐代择优,最终获得海豚群体的位置。将DPO算法用于BP网络初始权值、阈值的优化上,再将优化后得到的一组最优权值和阈值作为BP网络的初始权阈值,运用于测试样本的预测可以取得不错的效果。

Figure 2. The process of dolphins foraging
图2. 海豚群觅食的流程
3.3. DPO-BP算法的基本步骤
将DPO算法与BP神经网络这两者相结合,运用DPO算法确定一组BP网络的最优权阈值,可兼具DPO算法的全局寻优及局部细致搜索能力与人工神经网络的映射泛化能力。
DPO算法优化BP神经网络的基本步骤为:
Step1:设定DPO参数。初始化海豚群的位置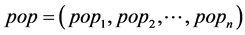 ,海豚群规模popsize,搜索维数为D,最大迭代次数为Maxgen,海豚个体的伙伴个数为teamsize,故第
,海豚群规模popsize,搜索维数为D,最大迭代次数为Maxgen,海豚个体的伙伴个数为teamsize,故第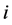 只海豚的位置可表示为:
只海豚的位置可表示为:
 式(2)
式(2)
其中,
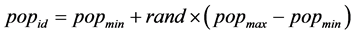 式(3)
式(3)
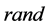 是在区间
是在区间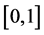 内均匀分布的一个随机数。
内均匀分布的一个随机数。
Step2:构造虚拟团队。海豚个体都会自发地选择各自的伙伴,组成虚拟团队。为了达到满意的寻优精度,定义以每只海豚 为自己虚拟团队的中心,分别计算海豚
为自己虚拟团队的中心,分别计算海豚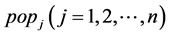 到海豚
到海豚 的距离
的距离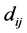 。一般情况下海豚个体选择距离相近的
。一般情况下海豚个体选择距离相近的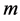 只海豚构建虚拟团队Team。
只海豚构建虚拟团队Team。
Step3:选取合适的适应度函数。在确定一组最优的BP神经网络的权值、阈值过程中,选择合适的目标(适应度)函数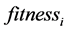 也是关键的环节。一般地,选用训练样本构建及训练BP网络,为了检测网络的优劣,通过测试样本对当前训练好的BP网络进行误差检测,由
也是关键的环节。一般地,选用训练样本构建及训练BP网络,为了检测网络的优劣,通过测试样本对当前训练好的BP网络进行误差检测,由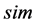 函数可以得到网络的预测输出
函数可以得到网络的预测输出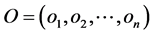 ;若将测试样本期望输出记为
;若将测试样本期望输出记为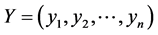 ;把预测输出和期望输出之差的均方误差值作为个体适应度值
;把预测输出和期望输出之差的均方误差值作为个体适应度值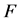 ,计算公式为:
,计算公式为:
 式(4)
式(4)
Step4:确定海豚群最优位置。根据各海豚团队中海豚个体的BP预测仿真值,由适应度函数公式确定每个团队的最优解 和最优位置
和最优位置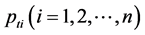 ,以及海豚群的最优解
,以及海豚群的最优解 和最优位置
和最优位置 。
。
Step5:更新海豚位置。海豚确定彼此间的伙伴关系后,还需不断的更新自己的位置,以期望获得“食物”的准确信息。由理论可知,前期需要快速了解“食物”的位置,因此,海豚可以快速的找到“食物”的大概位置,伙伴间形成包围式的搜索,而到了后期,“食物”的位置已经基本锁定,就应该细致搜索,最终确定“食物”的准确位置。数学描述为前期大范围搜索,易跳出局部最优解,后期细致搜索,为精确找出最优解。故引入一个动态的权值变量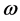 ,数值从0.7到0.4均匀衰减变化,则海豚个体的更新公式改写为
,数值从0.7到0.4均匀衰减变化,则海豚个体的更新公式改写为
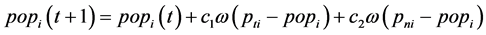 式(5)
式(5)
Step6:若迭代寻优次数达到Maxgen,则网络训练结束,得出海豚群最优位置(即一组最优权阈值),否则跳转Step2。
Step7:用此权值和阈值构建BP用于接下来的样本评价。
该组合算法DPO-BP在负荷预测中的具体流程见下图3所示。
4. DPO-BP在负荷预测中的应用
4.1. DPO-BP的基本参数设置
1) 网络初始化
仍选取上述数据作为网络的训练样本和测试样本,取训练样本个数为10个,即7月23到
8 月 5 日
(仅保留工作日)的10个样本数据,
8 月 6 日
的数据作为网络的测试样本。网络结构选取为3层,输入层的节点数为16,隐含层的节点数选取为11,输出层的节点数为1。
2) DPO算法参数初始值
设定海豚群的整体大小为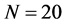 ,学习因子
,学习因子 ,
,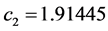 ,海豚群伙伴个数
,海豚群伙伴个数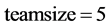 ,最大迭代次数
,最大迭代次数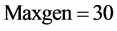 。
。
4.2. DPO-BP预测负荷的优越性
为了判断及证明DPO-BP算法预测模型的优越性,与PSO-BP相对比,对24个网络分别使用DPO-BP算法与PSO-BP算法进行训练,得到
8 月 6 日
的0:00~24:00点的负荷预测对比如图4所示。

Figure 3. The chart of DPO-BP algorithm for short-term load forecasting
图3. DPO-BP组合算法短期负荷预测流程
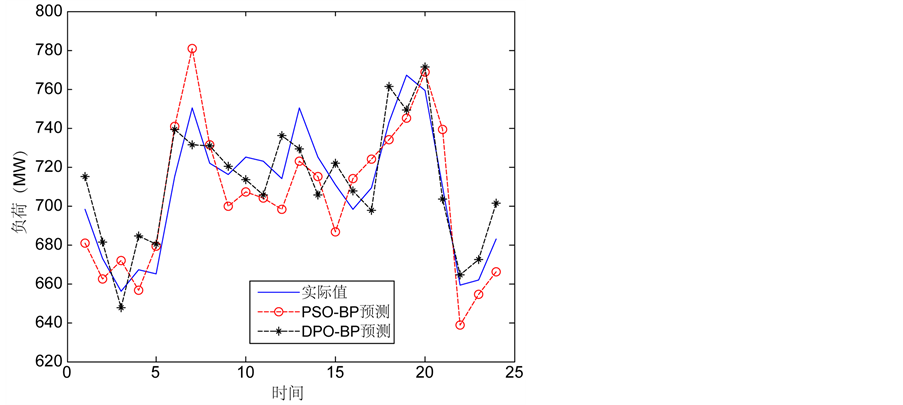
Figure 4. The 24 hours forecast comparison of the two algorithms
图4. 两种方法预测24小时对比
预测结果表明DPO-BP算法和PSO-BP的预测结果都要优于前述未经优化的BP算法。由图4可见,其中,PSO-BP的24小时负荷预测的最大误差出现在7点,误差是4.10%,DPO-BP的24小时负荷预测的最大误差出现在6点,误差是3.42%。比1.3节所述BP神经网络的24小时的预测误差最大5.7%相比,预测效果明显更优。经计算,PSO-BP算法的24小时平均绝对误差为2.41%,DPO-BP算法的24小时平均绝对误差为1.92%。DPO-BP的短期负荷预测误差要小于PSO-BP的预测误差,预测效果更好。
5. 结论
本文将人工海豚算法用于BP神经网络的优化,对指定日期的24小时电力负荷分别进行预测。由于人工海豚算法具有较高的收敛速度、寻优精度,将DPO-BP用于负荷的短期预测上的结果与PSO-BP算法进行对比分析。结果发现,DPO-BP算法的求解精度更高,预测效果更好。