宇航单机元器件随机振动疲劳分析

Fatigue Analysis of Aerospace Electronic Equipments under Random Vibration

摘要: 宇航单机在生命周期内要经历各种振动环境，在随机振动过程中，单机内的敏感元器件容易疲劳破坏而出现管脚断裂或焊点脱落。文章针对某型号宇航单机元器件管脚断裂情况，对其结构及元器件的几何模型进行了详细的有限元分析，获得随机振动工况下的均方根应力场，应用Miner疲劳损伤累计理论及三带宽技术，进行元器件管脚的疲劳分析，并对结构进行优化，再次分析得知结构改进后单机的疲劳安全裕度得到很大提高且通过了试验验证。结果表明了该疲劳分析方法的有效性。

Abstract: The aerospace electronic equipment undergoes a variety of vibration environments throughout its life cycle. In the process of random vibration, the sensitive chips in the electronic equipment are prone to fatigue failure, and the fracture of the pins or the welding joints are broken out. In this paper, the fracture of the pin of the aerospace electronic equipment is discussed, and a de-tailed finite element analysis of the geometric model of the equipment structure and chips is car-ried out to obtain RMS stress field under random vibration conditions, and Miner’s cumulative fatigue damage theory and three bandwidth technique are used to analyze the fatigue of chips and its pins. After the structure optimization of the equipment, a detailed finite element analysis of the geometric model of the equipment structure and chips showed that the optimized structure safety margin has been greatly improved and verified by test. The results show that this method is an effective method for random vibration fatigue analysis of the aerospace electronic equipment.

1. 引言

宇航单机设备在制造、运输、发射等阶段都经历着不同振动环境的考验，尤其在可靠性试验验证阶段，单机需要经历最为严酷的鉴定级随机振动环境。为保证宇航单机设备的高可靠性，一般在设计阶段通过有限元仿真手段对其结构进行设计可靠性保证。随着计算机及仿真技术的发展，在产品的设计过程中通过计算机软件对不同设计方案进行仿真分析的需求越来越大，通过高性能计算机及相应的软件，便能快速实现设备随机振动仿真分析。通过对多个宇航单机设备的有限元分析与试验验证得知，宇航单机的结构件及印制板一般不会出现强度破坏或刚度不够等问题。随机振动试验表明最容易出现问题的是单机设备中的敏感元器件，如FPGA表贴、DIP双列直插式封装、BGA球阵列封装、钽电容器件等由于疲劳破坏而出现管脚断裂或焊点脱落等 [1] 。

宇航单机设备的结构形式较为复杂，有限元建模时，通常将PCB上的元器件用质量点等效替代分析。但是，该方法无法求取敏感元器件管脚的应力场，无法确认元器件最大失效位置。为了求取敏感元器件管脚的最大应力位置，需要建立详细的元器件有限元模型。假如元器件都不做等效处理而建立全部的详细有限元模型，整个模型将非常庞大，甚至超出计算机硬件计算能力而无法进行分析。考虑到某些宇航单机的结构形式，可以采用模块化解算依次进行求取。本文根据宇航单机的结构形式，采用模块化建模，对模块进行随机振动仿真分析，得到其工况下元器件管脚的应力。最后，应用Miner疲劳损伤累积理论及三带宽技术对元器件管脚进行疲劳寿命计算，判断单机结构设计的合理性。

2. Miner疲劳损伤累积理论与随机振动

2.1. Miner疲劳损伤累积理论

Miner线性损伤积累理论 [2] 认为，每经历一次应力循环，结构将消耗掉一部分的寿命，这里的应力循环是指随机振动引起的交变应力，该理论认为，结构在各种交变应力下的疲劳损伤是相互独立的，并且总损伤可以线性累积起来，当总疲劳损伤超过产品的疲劳极限后即造成疲劳破坏。用疲劳破坏率R表示已消耗结构寿命的百分比，如R = 0.5，表示实际应力循环已消耗掉结构疲劳寿命的一半，疲劳破坏率R [1] 定义如下：

$R=\sum \frac{n_i}{N_i}$ (1)

式(1)中， $n_1,n_2,n_3,\cdots$ 表示实际工况下结构所承受的应力循环次数； $N_1,N_2,N_3,\cdots$ 表示在指定条件下结构产生疲劳破坏前可承受的应力循环次数，一般需要经过大量的试件经受不同应力水平的疲劳试验测试确定，提取其绘制曲线，该曲线称为该材料的S-N曲线。

疲劳破坏率由R确定。当R < 1，表示在实际应力循环次数下结构不会产生疲劳破坏，且R越小，结构剩余疲劳寿命越多；当R ≥ 1，表示在实际应力循环次数下结构已经发生疲劳破坏 [1] 。

Miner线性损伤积累理论的成功之处在于它在工程上简便易用，且大量试验结果显示，结构发生疲劳破坏时的 ${\displaystyle \sum n_i/N_i}$ 均值确实接近于1 [3] 。而其他累积损伤理论和计算方法，要么计算过于复杂，要么并未给出所用参数的确定方法，要么必须进行大量的疲劳试验才能获取所需的计算参数，均难以应用于实际工程中，且计算精度也并不比Miner理论高，所以即使Miner理论自身并不完美，却一直在工程界广泛应用，尤其在随机载荷下，应力循环的大小次序完全是随机的，相邻两个应力循环由低到高与由高到低是等概率事件，削弱了载荷次序的影响 [3] 。本文采用Miner准则作为元器件管脚疲劳破坏的判据。

2.2. 随机振动及三带宽技术

2.2.1. 随机振动

随机振动，通常由大气湍流引起的抖振，时间长、频域宽，属于稳态宽幅随机振动 [4] ，是宇航单机设备在发射过程中都会经历的振动环境。在任意时刻，给定带宽内的所有频率自始至终都会出现在整个随机振动过程中，也就是说，当一个宇航单机设备经受频带为20 Hz~2000 Hz的随机振动环境时，设备在相同带宽内的所有谐振将同时受到激发。宇航单机设备的随机振动是地面力学环境试验中必须考核的一个工况，为避免与整星发生共振，通常将单机设备内部的印制板固有频率设计在100 Hz以上。通常随机振动的试验条件为3个方向每个方向各经受2 min的随机振动考核，印制板共经受的振动循环次数约在36,000次(以印制板固有频率为100 Hz计算)以上，可知在整个试验过程中印制板要发生几万次的往复运动。根据随机振动试验经验可知，在随机振动过程中，通常会发生元器件管脚断裂或焊点开裂等故障，对其断面分析可知，大多数是由于疲劳造成的。所以，宇航单机设备一般都应进行随机振动疲劳分析。

随机振动中，结构的疲劳分析主要有时域和频域两种方法。与频域分析方法相比，时域分析耗时较长，而且有可能出现不收敛的情况；而基于功率谱密度(PSD)的频域分析方法可以用相对较少的时间获得较为保守的结果，而且也不会出现不收敛的情况 [4] 。

一般通过统计特性来描述随机振动，就像确定性振动一样，其也有确定的输入与输出关系。分析随机振动的过程就是确定具有统计特性的输入与具有统计特性的输出间的确定性关系的过程 [1] 。线性各态历经平稳随机振动的系统可用式(2)表示：

$M\left\{\ddot{u}\left(t\right)\right\}+C\left\{\stackrel{\dot{}}{u}\left(t\right)\right\}+K\left\{u\left(t\right)\right\}=\left\{F\left(t\right)\right\}$ (2)

就像确定性振动一样，通过模态坐标变换和模态叠加理论，可以获得系统的频响函数，具体见式(3)所示：

$H\left(i\omega \right)={\displaystyle \underset{r=1}{\overset{n}{\sum }}\frac{\left\{{\phi }_r\right\}{\left\{{\phi }_r\right\}}^T}{-{\omega }^2{m}_r+k_r+i\omega c_r}}$ (3)

其中， ${\phi }_r,m_r,k_r,c_r$ 分别为模态向量、模态质量、模态刚度和模态阻尼。

由杜哈梅积分和随机过程 [5] 可知，随机振动的输入功率谱密度 $G_{in}\left(\omega \right)$ 与输出功率谱密度 $G_{out}\left(\omega \right)$ 之间的关系如式(4)所示，该过程较为繁琐，详细推导过程可见文献 [6] 。

$G_{out}\left(\omega \right)={\left|H\left(i\omega \right)\right|}^2{G}_{in}\left(\omega \right)$ (4)

结果通过均方根加速度、均方根应力、均方根位移来评价。对于各态历经平稳随机过程，数学期望E(u) = 0，则：

方差： ${\sigma }_u^2=E\left[{\left(u\left(t\right)-E\left(u\left(t\right)\right)\right)}^2\right]=E\left(u^2\left(t\right)\right)-E^2\left(u\left(t\right)\right)=E\left(u^2\left(t\right)\right)$

且有自相关函数： $R_u\left(0\right)=E\left[u\left(t\right)\cdot u\left(t\right)\right]=E\left[u^2\left(t\right)\right]={\sigma }_u^2$

响应的均方值为： ${\bar{u}}^2=E\left(u_2\right)=R_u\left(0\right)={\displaystyle {\int }_{f_1}^{f_2}{G}_{out}\left(\omega \right)\text{d}\omega }$

则响应的均方根为： ${\sigma }_u=\sqrt{{\bar{u}}^2}=\sqrt{{\displaystyle {\int }_{f_1}^{f_2}{G}_{out}}\left(\omega \right)\text{d}\omega }$

2.2.2. 基于高斯(正态)分布的三带宽技术

高斯分布即正态分布，是一种常见的重要分布，根据概率论中心极限定理，如果一个随机现象由众多随机因素引起，且每个随机因素在总的现象变化中起不到显著的作用，就可以认为描述该随机现象的随机变量近似地服从高斯分布 [1] 。均值为零的高斯分布的概率密度可用式(5)表示，概率曲线如图1所示。

$p\left(x\right)=\frac{1}{\sigma \sqrt{2\text{π}}}{\text{e}}^{-\frac{x^2}{2{\sigma }^2}}$ (5)

其中，x为瞬态随机变量，σ为均方根值(如均方根加速度、均方根应力、均方根位移等)。由图1可知其意义如下：瞬态随机变量在+1σ和−1σ之间的概率为68.3%，瞬态随机变量超出1σ的概率为31.7%；瞬态随机变量处于+2σ和−2σ之间的概率为95.4%，瞬态随机变量超出2σ的概率为4.6%；瞬态随机变量处于+3σ和−3σ之间的概率为99.73%，瞬态随机变量超出3σ的概率为0.27%。随机变量超出+3σ量级的可能性已经很小了，采用3σ水平评估已可满足工程要求。

三带宽技术 [6] 的基础是高斯分布，假定1σ水平的瞬时加速度作用在+1σ和−1σ之间的时间是68.3%，2σ水平的瞬时加速度作用在+2σ和−2σ之间的时间是(95.4~68.3)%即27.1%，+3σ水平的瞬时加速度作用在+3σ和−3σ之间的时间是(99.73~95.4)%即4.33%。这些数值可表示为式(6)三个分段 [2] ：

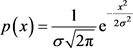
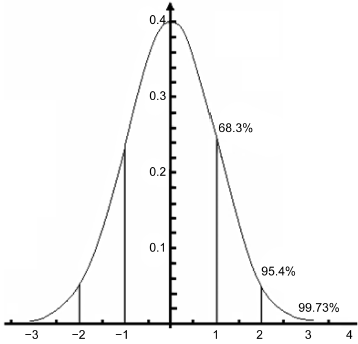
Figure 1. Gaussian distribution (Normal distribution) (σ = 1)

图1. 高斯(正态)分布(σ = 1)

$\begin{array}{l}\mathrm{1\; \sigma \; 数值发的生时间是68.3\%}\\ \mathrm{2\; \sigma \; 数值发的生时间是27.1\%}\\ \mathrm{3\; \sigma \; 数值发的生时间是27.1\%}\end{array}\}$ (6)

3. 元器件管脚随机振动疲劳分析实例

3.1. 元器件管脚随机振动疲劳失效分析实例

某型号宇航单机由支架结构框、PCB基板、元器件及元器件管脚等组成。激励源为鉴定级随机振动试验条件，具体输入详见下表1所示。

该单机完成X向和Y向随机振动后，分别加电测试产品正常，后完成Z向随机振动后进行加电测试，发现单机无电流输出。经过故障分析，X光检测，发现单机印制板上一元器件管脚断裂，见图2所示。

3.2. 有限元模型建模及仿真分析

宇航单机在随机振动工况下一般结构框、印制板等结构件不会出现断裂失效，而布置在印制板上的元器件却很容易出现管脚失效。一般建模时不考虑元器件的细节，简单以质量点代替，这时随机振动仿真结果无法得到元器件管脚应力信息，只有质心处的加速度、速度、位移等信息，而这些数据无法直接作为判断器件管脚失效的依据。为了求取元器件管脚断脚处的最大应力，需要对该器件建立详细的元器

Table 1. Qualification conditions for random vibration test

表1. 随机振动试验鉴定级条件

Figure 2. The fracture of the pin in the chip (the 1st pin)

图2. 元器件管脚断裂拆卸情况(1脚断裂)

件有限元模型，其余元器件全部做等效质量点处理。有些文献利用均方根加速度信息，作为器件过载激励，将该过载激励载荷直接施加到印制板上。由于印制板的工作状态与其单机在随机振动条件下的工作状态差别较大，且边界条件无法控制，使得该处理方法实施操作有困难。

模态分析是随机振动分析的基础，所以在进行随机振动分析之前需要先求解模块的有效模态振型。通过NX Nastran进行建模并模态分析得到模块的基频为211.5 Hz，见图3所示。

通过输入表1中的加速度功率谱，进行随机振动响应仿真得到管脚均方根应力最大位置，详见图4所示。

由图4可知，在随机振动过程中，元器件管脚可受到的最大均方根应力为157.64 MPa。

3.3. 元器件管脚的疲劳寿命计算

3.3.1. 应用三带宽技术计算管脚发生疲劳所需的应力循环次数

根据可伐合金“S—N疲劳寿命曲线”和公式(7) [2] ，分别计算在 $1\sigma$ 、 $2\sigma$ 、 $3\sigma$ 应力情况下元器件管脚发生疲劳破坏所需的应力循环次数，其中，N₂ = 1000为参考点2所对应的疲劳循环次数；S₂ = 579 MPa为参考点2的疲劳应力；S₁为计算所得的 $\text{n}\sigma$ 应力；b = 6.4为应力集中因子为2的可伐合金疲劳曲线的斜率 [2] ，详细曲线见图5所示。

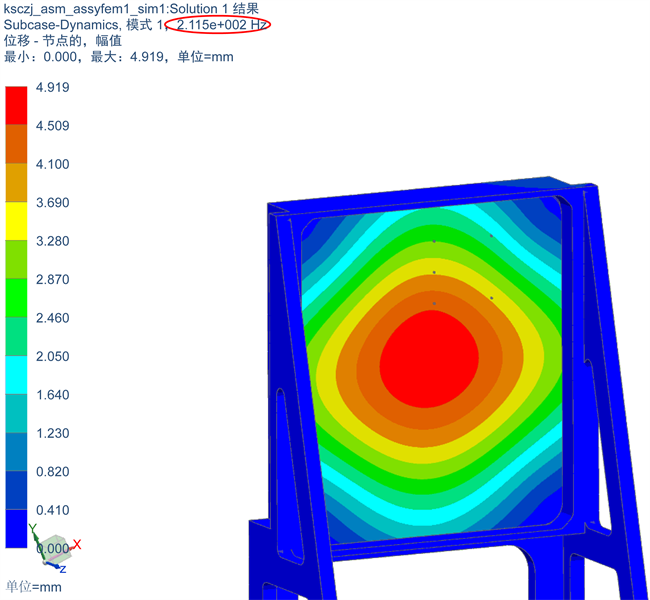
Figure 3. The first order mode shapes of fault module

图3. 故障模块第一阶模态振型图

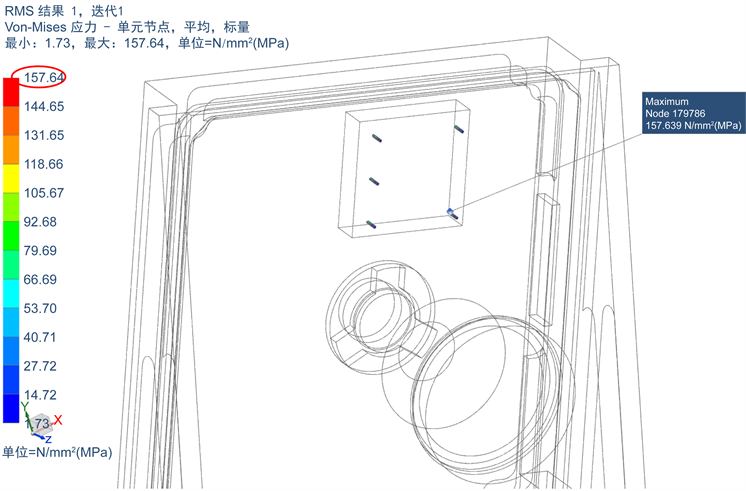
Figure 4. RMS stress field under random vibration conditions of the electronic equipment

图4. 某型号宇航单机随机振动器件管脚处均方根应力图

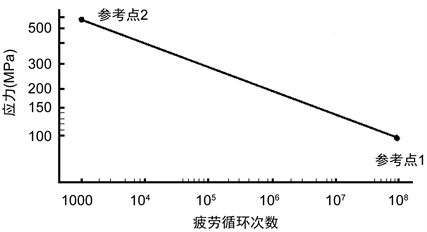
Figure 5. The S-N curve of kovar

图5. 元器件管脚可伐合金材料S-N曲线

$N_1=N_2{\left(\frac{S_2}{S_1}\right)}^b$ (7)

式中：S₂ = 579 MPa (柯伐合金管脚的极限抗拉强度)；

N₂ = 1000 (柯伐合金管脚在极限抗拉强度下故障前经受1000个循环)；

S₁ = 157.64 MPa (管脚所受的最大均方根应力)

b = 6.4 (柯伐合金疲劳曲线的斜率)；

则有：

$N_{1\sigma }=1000\times {\left(\frac{579}{1\times 157.64}\right)}^{6.4}=4131213$

$N_{2\sigma }=1000\times {\left(\frac{579}{2\times 157.64}\right)}^{6.4}=48920$

$N_{3\sigma }=1000\times {\left(\frac{579}{3\times 157.64}\right)}^{6.4}=3652$

其中， $N_{1\sigma }$ 、 $N_{2\sigma }$ 、 $N_{3\sigma }$ 分别为 $1\sigma$ 、 $2\sigma$ 、 $3\sigma$ 应力情况下结构发生疲劳破坏所需的应力循环次数。

3.3.2. 元器件管脚实际应力循环次数

实际故障出现在第三个方向2 min随机振动情况下，管脚出现断裂。通过仿真计算该模块结构形式下印制板的基频为211.5 Hz， $1\sigma$ 、 $2\sigma$ 、 $3\sigma$ 应力情况下可能发生的应力循环次数为：

$n_{1\sigma }=211.5\text{Hz}\times 60\times 6\min \times 0.683=52003.62$

$n_{2\sigma }=211.5\text{Hz}\times 60\times 6\min \times 0.271=20633.94$

$n_{3\sigma }=211.5\text{Hz}\times 60\times 6\min \times 0.0433=3296.862$

其中， $n_{1\sigma }$ 、 $n_{2\sigma }$ 、 $n_{3\sigma }$ 分别为 $1\sigma$ 、 $2\sigma$ 、 $3\sigma$ 应力情况下结构实际发生的应力循环次数。

根据公式(1)计算该元器件管脚的破坏率R

$R=\frac{n_{1\sigma }}{N_{1\sigma }}+\frac{n_{2\sigma }}{N_{2\sigma }}+\frac{n_{3\sigma }}{N_{3\sigma }}=1.337>1$ ，

说明该元器件的管脚在随机振动过程中已经出现疲劳破坏，理论分析结果与滤波器断裂管脚部位的失效分析结果相符。

3.3.3. 结构改进及验证

由器件失效机理分析可知，在振动过程中是因为器件与印制板之间的相对变形造成器件在高应力状态下连续工作，导致疲劳失效。为了获取满意的疲劳寿命，需要将器件与印制板之间的相对变形降为最小。减小相对位移的措施主要局部加固元器件周围的印制板，工艺点胶措施使器件本体与印制板相连，分担管脚承担的载荷。根据加工成本、工艺措施，经过几轮的分析计算，最终对采取了结构合理的优化，元器件本体降低安装高度，四角采用点环氧胶处理等改进措施，改进后的第一阶模态振型图和均方根应力云图见图6、图7所示。

从图7可以看出改进后模块的最大应力得到极大的降低，管脚应力环境得到极大的改善。根据公式(7)再次对管脚的疲劳寿命进行计算验证。

$N_{1\sigma }=1000\times {\left(\frac{579}{1\times 96.57}\right)}^{6.4}=95093871$

$N_{2\sigma }=1000\times {\left(\frac{579}{2\times 96.57}\right)}^{6.4}=1126057$

$N_{3\sigma }=1000\times {\left(\frac{579}{3\times 96.57}\right)}^{6.4}=84058$

由于结构局部加固，该结构基频提高到249.4 Hz (见图6)，验证完成三个方向上共6分钟的随机振动的疲劳损伤情况，其 $1\sigma$ 、 $2\sigma$ 、 $3\sigma$ 应力情况下可能发生的应力循环次数：

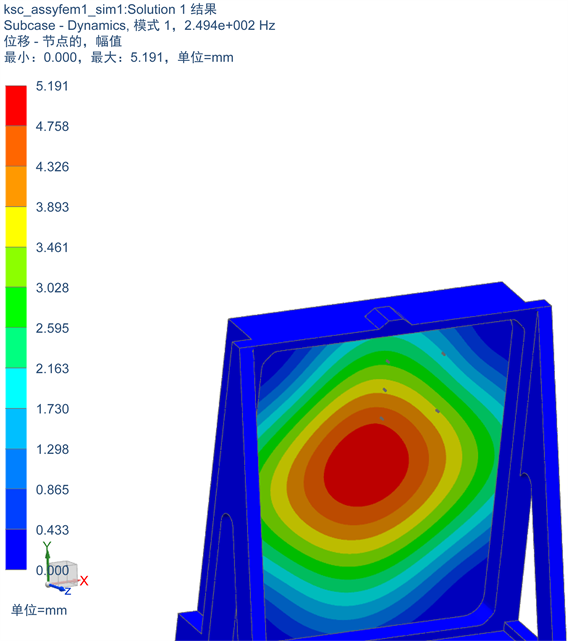
Figure 6. The first order mode shapes of the improved module

图6. 改进后的第一阶模态振型图

$n_{1\sigma }=\text{249}\text{.4Hz}\times 60\times 6\min \times 0.683=61322.5$

$n_{2\sigma }=\text{249}\text{.4Hz}\times 60\times 6\min \times 0.271=24331.5$

$n_{3\sigma }=\text{249}\text{.4Hz}\times 60\times 6\min \times 0.0433=3887.6$

计算该元器件管脚的破坏率R

$R=\frac{n_{1\sigma }}{N_{1\sigma }}+\frac{n_{2\sigma }}{N_{2\sigma }}+\frac{n_{3\sigma }}{N_{3\sigma }}=0.0685,$

远小于1，可知6分钟随机振动仅消耗其疲劳寿命的1/14。说明该种结构形式下元器件的管脚的疲劳安全裕度很高。该宇航单机已顺利通过了试验验证。

4. 结论

本文简要介绍了Miner疲劳损伤累积理论，用于随机振动疲劳分析的高斯分布三带宽技术，随机振动理论，宇航单机设备有限元建模及分析技术。以某型号宇航单机设备为例，介绍了宇航单机元器件管

Figure 7. RMS stress field of the improved module

图7. 改进后的均方根应力云图

脚随机振动疲劳失效分析的流程：对单机模块中出现随机振动疲劳故障的元器件及管脚进行详细建模；通过有限元仿真计算单机基频；分析其随机振动情况，获得元器件管脚处最大均方根应力值；计算元器件管脚的疲劳破坏率R值；判断其是否疲劳失效；若R > 1即失效，对单机结构形式或元器件安装方式进行合理优化，直到最终计算的疲劳破坏率R < 1，元器件管脚不会发生疲劳破坏。通过该宇航单机的随机振动疲劳失效分析过程验证了文章所述疲劳分析方法的有效性，为宇航单机设备工程设计中判断敏感元器件管脚在随机振动工况下是否产生疲劳失效提供了一个思路。