基于粒子群算法的风电系统调峰策略研究

Study on Peak-Load Control Strategy for Wind Power System Based on Particle Swarm Algorithm

摘要: 风电的随机波动特性对风电并网系统的负荷调峰特性产生影响，因此开展其调峰策略研究对确保风电系统的安全经济运行具有重要作用。本文在分析风电并网对系统调峰方式产生影响的基础上，从最大限度消纳风电角度出发，基于使火电、水电和抽水蓄能参与调峰发电成本最小化目标函数，建立了风电系统的调峰策略优化模型。同时利用粒子群算法研究了该优化模型的求解方法。最后利用所研究调峰策略优化方法进行了风电并网局部电力系统调峰策略的仿真研究，不仅得到了该地区基于火电、水电和抽水蓄能的联合调峰策略，而且验证了所提优化模型的合理性。

Abstract: The characteristic of peak-load regulation influenced by random vibration of wind power is different from the power system without the integration of wind power. So exploring peak-load regulation method plays a very important role for keeping power grid integrated with wind power operate in security and economy. In this paper, the demand variety of peak-load regulation led by wind power integration is discussed in the first. Then, taking the aim at consuming wind power as maximum as possible, and taking the minimal generation cost of thermal power, hydropower and pumped storage which are used to regulate the peak-load as optimal object function, the optimal model for peak-load control is established. At the same time, the solution method for the optimal model is developed based on particle swarm algorithm. Finally, the proposed optimal model is used to simulate the peak-load control strategy for a region wind power system. Not only the cooperative peak-load control strategy based on thermal power, hydropower power and pumped storage is arrived in, but also the rationality and feasibility of the optimal model is validated as well.

1. 引言

进入21世纪以来，风电蓬勃发展，装机容量一直保持高速增长 [1] ，但风电的随机间歇性及预测精度低等特性，使风电并网面临诸多挑战。其中，风电并网使系统调峰问题凸显 [2] [3] 目前，已有文献对风电并网系统的负荷调峰问题进行了研究。其中，一部分集中在系统调峰能力和调峰充裕度的评估方面。例如，文献 [4] [5] 分别分析了西北电网和京津唐电网在风电并网后的系统调峰特性，并基于确定性方法给出了计算其调峰能力的方法；文献 [6] [7] [8] 则从评估系统调峰能力的裕度角度，分别基于序贯蒙特卡洛模拟方法和非序贯蒙特卡洛模拟方法，研究了评估大规模风电接入后系统调峰充裕性的方法。另一部分则集中在如何确定风电并网系统负荷调峰策略的方法方面。例如，文献 [9] [10] [11] 以发电成本最小为目标函数，以功率平衡和调峰容量为约束条件，建立了调峰模型并给出了调峰策略仿真结果。其中文献 [9] 基于系统调峰出力和机组爬坡速率构建了最大化风电收益的优化模型；文献 [10] 考虑水电机组的调峰作用，提出了常规机组的出力优化模型；文献 [11] 以发电成本最小、省内水电不弃水方式参与调峰并尽可能多地消纳特高压电力为目标，建立湖北电网火电、水电、抽水蓄能和特高压联合调峰的混合整数线性规划模型。但上述调峰策略优化模型没有考虑潮流安全约束，所确定的调峰策略可能会导致系统潮流越限，因此应用于实际系统还存在一定不足。

针对上述问题，本文提出了一种兼顾系统经济性和安全性的调峰策略优化模型。该模型以调峰机组运行成本最小为目标函数，以调峰容量与潮流安全约束为约束条件，同时研究了利用粒子群算法求解风电并网系统调峰机组最优出力组合的方法。研究结果表明该方法不仅能够充分利用各类型调峰机组的调节特性，提升系统的安全性和经济性。

2. 风电系统的调峰特性

系统的调峰需求为日负荷波峰值P_dmax与日负荷波谷值P_dmin的峰谷差，即 $P_{\text{mn}}=P_d{}_{\text{max}}-P_d{}_{\text{min}}$ 。然而，当大规模风电接入系统后，由于风电和负荷均具有随机性，将增加系统日调峰需求的不确定性。风电并网对系统调峰需求的影响，取决于图1所示的等效负荷的峰谷差。图中的等效负荷通常用式(1)所述P_G-w(t)表示，其中，P_L(t)为系统负荷，P_w(t)为风电出力。

$P_{G\text{-}w}\left(t\right)=P_L\left(t\right)-P_w\left(t\right)$ (1)

风电并网系统的调峰需求表示 $P_{\text{mn}}^{*}=P_{G\text{-}w\text{\_max}}\left(t\right)-P_{G\text{-}w\text{\_min}}\left(t\right)$ 。根据风电出力对系统负荷调峰影响程度

的不同，一般将风电出力的调峰特性分为反调峰、正调峰与过调峰 [12] 。其中，反调峰是指风电出力变化趋势与系统负荷曲线变化趋势相反，导致系统调峰需求增大；正调峰指风电出力变化趋势与系统负荷曲线变化趋势基本一致，接入风电后系统调峰需求减小；过调峰属于正调峰的一种特殊情形，即风电接入后系统等效负荷曲线与未接入风电的负荷曲线相比，峰谷发生倒置。

3. 基于粒子群算法的调峰策略优化

3.1. 调峰策略的优化模型

机组的调峰能力可以定义式(2)所示的机组可调容量与额定容量的比值，即：

${\alpha }_i=\frac{P_{Gi\max }-P_{Gi\min }}{P_{Gi\max }}\times 100\%$ (2)

式中：α_i为常规机组i的调峰深度；P_Gimax为常规机组i的最大出力，可以取为机组的额定容量；P_Gimin为常规机组i的最小出力。

电力系统中常用的调峰机组包括水电机组、火电机组和抽水蓄能。不同调峰机组因调峰方式不同，调峰能力也有所差异。火电机组的调峰方式有两种：启停方式、调荷方式。单机容量低于100 MW的火电机组一般采用启停调峰，但是，启停成本较高，实际中可能会造成其他问题，因此较大容量的机组一般采用调荷方式，它所对应的可调容量为最大出力(额定出力)与最小技术出力的差值。不同容量火电机组的最小技术出力如表1所示 [13] 。

水电机组按水库的调节性能可分为无调节、日调节、周调节、年调节和多年调节水电机组。除无调节水电机组外，由于启停迅速，有调节水电机组是理想的调峰机组。

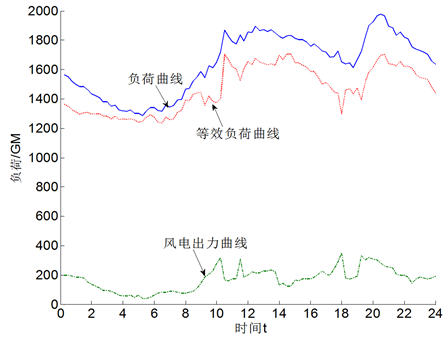
Figure 1. Schematic diagram of peak-shaving

图1. 调峰需求示意图

Table 1. Minimum technical output of thermal generators

表1. 火电机组最小技术出力

抽水蓄能机组可以在抽水和发电2个运行状态之间转换，是具有灵活调节能力的调峰电源。当负荷处于低谷时，抽水蓄能机组可以抽水，以位能的形式储存能量；在负荷高峰时，抽水蓄能机组利用上水库储存的水发电，其机组的调峰能力接近200%。

若以使风电系统调峰机组发电成本最小作为优化目标函数，同时以调峰机组的机组出力范围和风电

系统的潮流安全作为等式和不等式约束条件，可构建式(3)和式(4)所示的风电并网系统的调峰策略优化模型。

$\min F={\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N_h}{\sum }}{C}_{hi}\left(t\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N_c}{\sum }}\left[[C_{ci}^1\left(t\right)+C_{ci}^2\left(t\right)\right]}}}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N_w}{\sum }}{C}_{si}\left(t\right)}}$ (3)

s.t.

$\{\begin{array}{l}{P}_{gj}+\Delta P_{Gi}-P_{li}-U_i{\displaystyle \underset{j=1}{\overset{N}{\sum }}{U}_j\left(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right)}=0\\ Q_{gj}-Q_{li}-U_i{\displaystyle \underset{j=1}{\overset{N}{\sum }}{U}_j\left(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij}\right)}=0\\ {\displaystyle \underset{k=1}{\overset{N_G}{\sum }}{\alpha }_k{P}_{Gk\max }}\ge {\displaystyle \underset{m=1}{\overset{N_{WG}}{\sum }}\Delta P_{mGW\max }}+\Delta P_{L\max }\\ P_{gi\min }\le P_{gi}\le P_{gi\max },i\in N_g\\ U_{i\min }\le U_i\le U_{i\max },i\in N_U\\ Q_{gi\min }\le Q_{gi}\le Q_{gi\max },i\in N_Q\end{array}$ (4)

式(3)中：T为系统调度周期内的总时段数；N_h为火电机组数；N_c为抽水蓄能机组数；N_w为水电机组数； $C_{hi}\left(t\right)$ 为火电机组i在t时段发电费用； $C_{ci}^1\left(t\right)$ 和 $C_{ci}^2\left(t\right)$ 分别为抽水蓄能机组i处于发电工况和抽水工况时在t时段的启动费用； $C_{si}\left(t\right)$ 为水电机组i在t时段发电费用。

式(4)中：N为系统节点集合；N_G为系统的调峰机组节点集合；N_WG为系统的并网风电节点集合；N_g为系统发电机节点集合；N_U为系统中枢电压节点集合；N_Q为系统的无功补偿调节节点集合；P_gj为系统节点j的注入有功；Q_gj为系统节点j的注入无功； $\Delta P_{Gi}$ 为系统的有功调节增量；P_li、Q_li分别为系统负荷的有功和无功；U_i和U_j分别为系统节点i和j的节点电压幅值；G_ij、B_ij和θ_ij分别为节点i、j之间的电导、电纳和电压相角差；α_k为火电、水电或抽水蓄能等调峰机组k的调峰能力；P_Gkmax为调峰机组k的最大技术出力有功容量； $\Delta P_{mGW\max }$ 为系统风电并网节点m的最大风电有功变化； $\Delta P_{L\max }$ 为系统负荷的最大峰谷差；P_gi为调峰机组的输出功率；P_gimax、P_gimin分别为各调峰机组有功调节的上限和下限；U_imax、U_imin分别为系统各电压重要节点的上下限；Q_gimax和Q_gimin分别为系统无功调节节点无功调节装置无功调节上下限。

由式(3)和式(4)可知，利用上述优化模型不仅可以在确定风电系统调峰策略的同时，实现调峰机组的经济运行，而且能够保证系统的静态安全运行。

3.2. 基于粒子群算法的求解方法

利用式(3)和式(4)优化风电并网系统的调峰策略属于多变量、多约束非线性规划问题。目前常用求解方法主要包括常规数学优化和现代启发式两种求解算法。启发式求解属于人工智能求解，具有原理简单、搜索能力强等特点，因此在工程寻优问题中得到了广泛应用。但是，启发式算法进行寻优也存在寻优早熟和陷入局部收敛等问题，由此，本文基于对避免寻优早熟和局部收敛具有较好效果的粒子群算法研究了式(3)和式(4)所示调峰策略优化模型的求解方法 [14] [15] 。

该方法以式(3)所示目标函数作为粒子群算法的适应度函数，基于粒子群算法寻优步骤在由各调峰机组调峰出力范围确定的可行域中，寻优满足式(4)约束条件的调峰机组最优出力组合，具体流程如图2所示。由图可知求解步骤和过程如下：

步骤1，基于优化目标风电系统，建立风电并网系统的潮流计算模型，初始化式(3)和式(4)所示优化模型参数。

步骤2，设置反映粒子自身经验认知能力和社会经验认知能力的权重参数c₁、c₂，通常可设为2；设置粒子保持已有寻优速度的惯性权重参数 $\omega \in \left[0,1\right]$ ，通常可设为0.8；令寻优目标的搜索空间维度等于风电并网系统的调峰机组节点数N_G，根据调峰机组的调峰能力定义寻优空间S_n；设向量x_i为寻优粒子，其分量 $x_{ij}\left(j=1,2,\cdots ,N_G\right)$ 表示调峰机组的有功增量，定义粒子的数目为m，并在寻优空间S_n中随机生成各

Figure 2. Flow chart of the optimal model solution based on particle swarm algorithm

图2. 粒子群算法的优化模型计算流程

粒子的初始分量 $x_{ij}\left(0\right)\left(i=1,\cdots ,m\right)$ ，同时随机生成各粒子的初始寻优速度v_i(0)；初始化各粒子对目标函数的适应值fit_i为无穷大，初始化粒子群的最优目标函数适应值值Fit为无穷大；设寻优搜索的最大迭代次数为N_max，同时设迭代次数n的初值为1。

步骤3，将各粒子分别代入潮流计算模型，基于潮流求解程序进行潮流分析计算，判断潮流是否满足约束条件，若满足，则执行步骤4；若不满足约束条件，则执行步骤7。

步骤4，根据潮流计算结果，利用式(3)所示目标函数分析当前迭代次数的各粒子适应值fit_i(n)。

步骤5，如果fit_i(n) < fit_i，则fit_i = fit_i(n)，并且令P_i = x_i(n)，否则保持fit_i与P_i不变，其中P_i为第i个粒子截止到迭代次数n所搜索到的最优空间位置。

步骤6，如果fit_i的最小值min[fit_i] < Fit，则Fit = min[fit_i]，并且更新min[fit_i]对应的粒子为全局最优粒子x_G，否则保持Fit与x_G不变，其中，x_G为截止到迭代次数n时基于主动搜索的全局最优点。

步骤7，利用式(5)所示粒子的速度和位移更新公式计算粒子在第n + 1次迭代次数的空间位置，式中，rand(1)是均匀分布在区间[0, 1]的随机数，目的是为了使粒子能够以等概率的加速度飞向粒子自身最好位置和粒子全局最好的位置。

$\{\begin{array}{l}{v}_i\left(n+1\right)=\omega \times v_i\left(n\right)+c_1\times rand\left(1\right)\times \left(P_i-x_i\left(n\right)\right)\\ +c_2\times rand\left(1\right)\times \left(x_G-x_i\left(n\right)\right)\\ x_i\left(n+1\right)=x_i\left(n\right)+v_i\left(n+1\right)\end{array}$ (5)

步骤8，如果n + 1 < N_max，则n = n + 1，返回步骤3进行下一次迭代次数的计算，直到迭代次数达到N_max，输出最优解。

4. 仿真研究

安徽电网的风电建设规模近年来得到了迅速发展，本文以安徽某地区风电并网的电力系统作为研究对象，研究利用所提优化模型确定该地区风电并网调峰策略的可行性。该地区风电系统的总装机容量为1133.67 MW，其中，4台火电机组的装机容量为92 MW、1台水电机组的装机容量为1.87 MW、1座抽水蓄能电站的装机容量600 MW、9座风电场的总装机容量为439.8 MW。由于该地区火电机组的单机容量不超过20 MW，因此依据表1可知该地区火电备用调峰容量为73.6 MW。同时，由于水电机组装机容量太小而抽水蓄能调峰容量较大，因此不考虑水电机组作为调峰备用容量，而以抽水蓄能作为备用调峰容量，且其调峰容量可达1200 MW。典型日负荷曲线如图3所示，负荷峰值为1980.17 MW、峰谷差高达692.25 MW，考虑风电场的装机容量，该地区电网在风电并网后的极端逆调峰情况下，调峰的峰谷深度需求可达到1132.05 MW。

利用Matpower潮流计算程序建立该地区风电系统的潮流计算模型，以该地区风电系统的火电和抽水蓄能作为备用调峰容量，以典型日负荷曲线和图3(b)、图3(c)所示该地区与负荷曲线峰谷变化趋势相似或相反的风电并网功率作为已知量，令优化模型中最大迭代次数N_max = 500、随机生成个体数m = 50，不考虑调峰电源的功率爬坡约束，求解得到图3所示该地区电网在风电接入前后调峰电源的输出组合。

图3(a)的仿真结果表明，由于该地区抽水蓄能装机容量大，且由于抽水蓄能调峰成本较火电调峰成本低，因此，风电并网前，利用所研究调峰策略优化模型得到的该地区调峰策略是通过抽水蓄能实现负荷调峰。对比图3(a)和图3(b)、图3(c)可知，风电并网对地区电网的调峰产生影响，将增加系统的调峰需求。风电接入后的系统顺调峰或逆调峰中，在负荷峰谷偏差较大处，当抽水蓄能调峰输出到达极限值时，在所研究调峰策略优化模型的作用下火电将配合抽水蓄能进行联合调峰。

图4对比了风电接入前后的调峰发电成本。对比风电未接入和风电接入的顺调峰发电成本可知，由

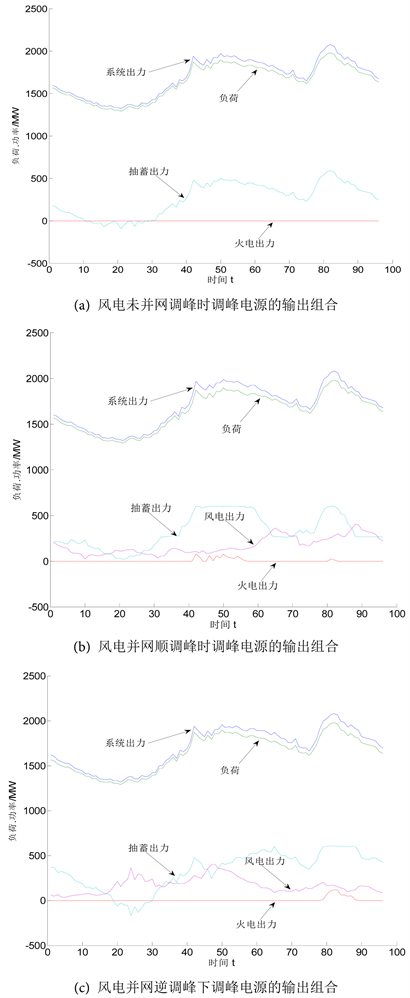
Figure 3. Combination of power output used to control peak-load with or without wind power integration

图3. 风电并网前后调峰电源的输出组合

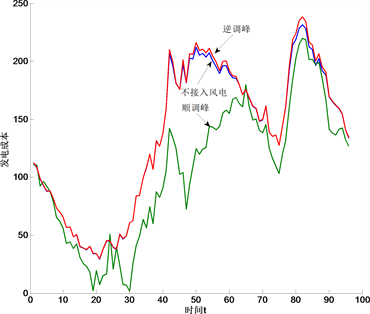
Figure 4. Cost comparison of power output used to control peak-load with or without the integration of wind power

图4. 风电并网前后的调峰发电成本对比

于顺调峰时风电并网功率的峰谷变化趋势与负荷峰谷变化趋于一致，因此，在并网风电功率的间接调峰

作用下，系统的调峰成本下降。风电接入后逆调峰和顺调峰的调峰成本的对比表明，由于逆调峰时风电并网功率的峰谷变化趋势与负荷峰谷变化趋势相反，因此，在并网风电功率的反用下，系统调峰深度的增加导致调峰成本增加。而对比风电接入与风电未接入时的调峰成本可知，所研究调峰策略优化模型可在满足系统调峰需求的同时，有效提高系统的运行经济性。同时，基于调峰策略优化求解的潮流计算结果表明，所研究调峰策略优化模型由于考虑了潮流安全约束条件，因此避免了调峰过程中潮流越限情况。由此可见，本文所研究优化模型能够兼顾系统运行安全经济性。

5. 结论

研究风电并网系统的负荷调峰策略对于提高系统的安全经济运行具有重要作用。本文从综合考虑风电系统调峰运行经济性和系统运行安全性角度出发，采用粒子群算法研究了风电并网系统的调峰策略的优化模型，仿真验证了该模型的有效性。不仅可以保证系统调峰的安全运行，而且能够提高调峰运行经济性。但如何在优化模型中建立考虑调峰机组爬坡特性和提高寻优算法的求解速度是该优化模型需要进一步深化的研究工作。

基金项目

国家重大研究发展计划资助项目(2017YFB0902904)。