1. 引言
单个智能体已很难适应越来越复杂的任务,而多智能体系统则可以通过多个智能体的信息交互与合作,解决较为复杂的任务。目前,多智能体系统被广泛应用于无人机编队、自主水下航行器、网络同步、水雷布阵等各个领域,吸引了众多学者的关注。一致性是指随着时间的演化,一个多智能体系统中所有的智能体的某个或者某些状态趋于一致,是多智能体实现协同合作、完成共同任务的基础 [1] [2] 。
多智能体一致性问题大多是在一阶和二阶系统中进行的 [3] [4] [5] [6] [7] ,但在某些特定环境下,研究高阶多智能体系统的一致性却更有现实意义。例如,当鸟群在飞行时,如果其中一个个体突然察觉到危险或食物,在这种环境下,鸟群如要快速达成共识,不仅需要它们的相对位置和速度,而且也需要了解它们的加速度 [8] 。为此,Ren等在文 [8] 中提出了如下描述高阶多智能体系统模型并研究了该系统的一致性问题。
(1)
其中,
是控制输入,满足
(2)
这里
是外部耦合强度,
是内部耦合强度,
是关联矩阵,因此我们可以定义该系统的图结构
,其中,
,
,
,随后,虞文武等 [9] 也研究了上述高阶多智能体系统,并给出了其达成一致性的充要条件。
在实际应用中获取相对位置信息的难度远比获取相对速度信息的难度低,考虑到避免无法获取速度信息的影响,虞文武等 [10] 等在控制输入函数中引入了时滞。事实上,时滞的不可避免,通常多智能体系统总要收到处理时间延迟和信息交互时间延迟的影响 [11] ,因此研究时滞高阶多智能体系统的一致性问题,非常有现实意义。本文主要研究具有如下含有时滞的
阶多智能体系统。
(3)
其中,控制输入函数
如式(2)所示,
表示处理延迟。
受文 [9] 的启发,本文首先通过将系统(3)的一致性问题转化为
的线性时滞系统的稳定性,再通过构造Lyapunov泛函 [12] ,获得了在处理延迟
小于某个定值时,系统(3)可达成一致性的结果。最后用数值仿真给出了满足本文条件时,3个智能体构成的高阶智能体系统可以达成一致性。
2. 预备知识及引理
为了研究系统(3)的一致性,首先引入如下一致性的定义 [2] 。
定义1:称多智能体系统(3)达成
阶一致性,若对任意初始条件,系统(3)的解
满足

为了研究系统(3)的一致性,类似于文 [9] 定义Laplace矩阵
为
,
。
此时控制输入(2)可以表示成如下形式
(4)
由于
是一个主对角占优的实对称Laplace矩阵,记
个特征值为
,则有
。令
,
则可将系统(3)转化为
(5)
其中,
是状态向量。再令
,则系统(5)可写成
(6)
由于
是Laplace矩阵,故存在酉矩阵
[13] ,使得
。因此可得
记
,则
满足
(7)
或者
(8)
由定义1和上述系统转化过程,类似于文 [2] 定理4.2的证明可得如下引理。
引理1:
是连通图,则(3)达成一致性的充分必要条件是系统(8)的解
满足
(9)
3. 主要结果
下面给出本文的主要结果。
定理1:若矩阵
(
)的特征多项式均满足Routh-Hurtiwz判据,则当时滞
满足
时,系统(3)可达成一致性,这里
,
为矩阵
(
)的特征值的最小模。
证明:由引理1可知,只需证明系统(8)的解
满足(9)。为此,定义Lyapunov函数如下:
,显然,
为
上的正定函数。对任意
定义
下面分三步证明系统(8)的解
满足(9)。
第一步:证明对任意
,都存在
,当
时,系统(8)的解
在
上满足
(10)
事实上,对任意
,取
,则当
时,对任意的
,系统(8)两边从0到
积分可得
从而有
因此(10)成立。
第二步:证明当
时,存在
使得
,则对任意
都存在
,当
时,系统(8)的解
满足
(11)
由第一步证明可知,这样的
存在,并且
类似第一步的证明,由系统(8)可得
故对任意的
,取
即得(11)成立。
第三步:由第一步和第二步的结果可得,函数
沿系统(8)的轨线的全导数为
因此,当
时,对任意的
和
,都有
成立,这里
。这意味着系统(8)的解
满足(9)。定理得证。
4. 数值模拟
因为系统(6)的零解是渐近稳定性的当且仅当系统(3)可达成一致性。因此,这里对系统(6)的零解的渐近稳定性行为进行模拟,为此在系统(6)中取
,
,
,
容易计算Laplace矩阵
的非零特征根为1和2,且
分别为
和
满足Routh-Hurwitz判据。且容易计算
,
,
。 取时滞
,则由定理1可得系统(3)可达一致性。系统8)的解满足(9),如图1所示。
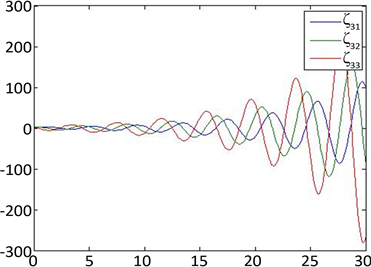
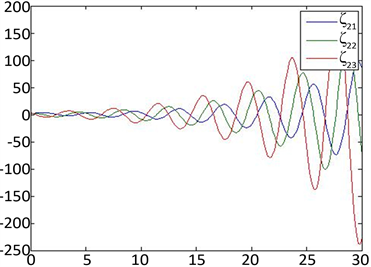
但在相同的初值条件下,如果时滞
比
大,例如
,系统(3)不能达到一致性,即系统(8)的解
不满足(9) (见图2)。
当时滞
时,数值模拟显示,系统(3)仍可达到一致性,这说明定理1仅为系统(3)达到一致性的充分条件。但在
时数值模拟显示,系统(3)不能达到一致性。通过多次数值模型,我们猜测在
之间会存在一个能够使得系统(3)达到一致性的临界时滞,甚至在该临界时滞附

 (a) 特征值
,初值为
时系统(8)的解的图像 (b) 特征值
,初值为
时系统(8)的解的图像
(a) 特征值
,初值为
时系统(8)的解的图像 (b) 特征值
,初值为
时系统(8)的解的图像
Figure 1. The trajectories of system (8) when
图1.
时系统(8)的解的图像
 (c) 特征值
,初值为
时系统(8)的解的图像 (d) 特征值
,初值为
时系统(8)的解的图像
(c) 特征值
,初值为
时系统(8)的解的图像 (d) 特征值
,初值为
时系统(8)的解的图像
Figure 2. The trajectories of system (8) when
图2.
时系统(8)的解的图像
近系统会出现Hopf分支最终导致周期解的出现,但目前我们还不能从理论上给予证明,这也是下一步我们要进行的工作。
基金项目
国家自然科学基金资助,项目编号:11401577。